Dopełnienie zbioru
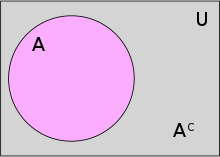
Dopełnienie zbioru, uzupełnienie zbioru[1][2][3][4] – zbiór wszystkich elementów (pewnego ustalonego nadzbioru), które do danego zbioru nie należą[5].
Definicja formalna[edytuj | edytuj kod]
Niech dany będzie zbiór zwany dalej przestrzenią[1][2][4][6], zbiorem uniwersalnym[4] lub uniwersum[4], oraz jego podzbiór Dopełnieniem zbioru nazywa się różnicę
oznaczaną zwykle symbolem [1][2][3][6] lub [2][4], a w starszych pozycjach także lub, jeśli jest znane, krótko (litera „c” w niektórych oznaczeniach pochodzi od ang. complement, dopełniać).
Niekiedy spotyka się również oznaczenie [6], jednak jeżeli jest zbiorem, na którym określono pewną (addytywną) strukturę algebraiczną, to może oznaczać wtedy
- Z definicji wynika, że dopełnienie zbioru zależy od wyboru przestrzeni.
- Korzystając z pojęcia dopełnienia zbiorów, różnicę zbiorów można zapisać w postaci:
Własności[edytuj | edytuj kod]
Dla dowolnego uniwersum prawdziwe są równości
Dla ustalonego i dowolnego zachodzi
co oznacza, że operacja dopełnienia jest inwolucją.
Prawdą jest też, iż zbiór i jego dopełnienie są rozłączne,
a ich suma daje całe uniwersum,
co oznacza, że jest rozbiciem zbioru
Dla danych zachodzą prawa de Morgana[7]:
Dodatkowo
- pociąga
Przykłady[edytuj | edytuj kod]
- Dopełnieniem zbioru w zbiorze jest zbiór
- Dopełnieniem zbioru liczb wymiernych w zbiorze liczb rzeczywistych jest zbiór liczb niewymiernych.
- Dopełnieniem prostej na płaszczyźnie euklidesowej jest suma dwóch rozłącznych otwartych półpłaszczyzn.
- Dopełnieniem zbioru w przestrzeni liczb naturalnych jest zbiór liczb naturalnych większych od natomiast w przestrzeni jest to zbiór
Przypisy[edytuj | edytuj kod]
- ↑ a b c Rozdział I (pdf). W: Kazimierz Kuratowski, Andrzej Mostowski: Teoria mnogości. T. 27. Warszawa-Wrocław: Monografie matematyczne, 1952, s. 18. [dostęp 2008-12-30].
- ↑ a b c d Kazimierz Kuratowski, Ryszard Engelking: Wstęp do teorii mnogości i topologii. Warszawa: Wydawnictwo Naukowe PWN, 2004, s. 16,17. ISBN 83-01-14215-4.
- ↑ a b Wojciech Guzicki, Piotr Zakrzewski: Wykłady ze wstępu do matematyki: wprowadzenie do teorii mnogości. Warszawa: Wydawnictwo Naukowe PWN, 2005, s. 15. ISBN 83-01-14415-7.
- ↑ a b c d e Kenneth A. Ross, Charles R.B Wright: Matematyka dyskretna. E. Sepko-Guzicka (tłum.), W. Guzicki (tłum.), P. Zakrzewski (tłum.). Warszawa: Wydawnictwo Naukowe PWN, 1996, s. 27–31. ISBN 83-01-12129-7.
- ↑ dopełnienie zbioru, [w:] Encyklopedia PWN [dostęp 2023-09-06].
- ↑ a b c Wiktor Marek, Janusz Onyszkiewicz: Elementy logiki i teorii mnogości w zadaniach. Warszawa: Państwowe wydawnictwo naukowe, 1975, s. 19.
- ↑ Angielski logik Augustus De Morgan odkrył przedstawione prawa rachunku zbiorów. Analogiczne prawa rachunku zdań sformułowano później, ale zwykło się je nazywać również nazwiskiem de Morgana Rozdział IV. Algebra zbiorów i relacji (pdf). W: Andrzej Mostowski: Logika matematyczna. T. 18. Warszawa-Wrocław: Monografie matematyczne, 1948, s. 100. [dostęp 2008-12-30].
































