Rozmaitość

Rozmaitość n-wymiarowa – uogólnienie pojęcia krzywej na więcej wymiarów. Zbiór punktów, wyposażony w geometrię, która ma lokalnie własności geometrii znanej z przestrzeni rzeczywistej -wymiarowej (przestrzeni euklidesowej). Wyposażenie w geometrię jest kluczowe – oznacza bowiem, że podane zostały wzory na obliczanie odległości między punktami, kątów między prostymi, pól powierzchni itp., przy czym lokalnie odległości między punktami są dane wzorami takimi jak w przestrzeni euklidesowej itd. Rozmaitość jest więc lokalnie identyczna z przestrzenią euklidesową. Lokalność zdefiniowana precyzyjnie oznacza, że każdy punkt rozmaitości ma otoczenie, nawet niewielkiego rozmiaru, które jest homeomorficzne z przestrzenią euklidesową [a][1]. Gdy rozmaitość przestaje być „płaska” – dla punktów rozmaitości bardziej od siebie odległych – to odległości są obliczane wzorami ogólniejszymi.
Wyróżnia się rozmaitości:
- jednowymiarowe: okręgi, elipsy, parabole i inne krzywe, przy czym nie należą do nich np. lemniskaty, jak lemniskata Bernoulliego (bo mają punkty przecięcia, które nie są lokalnie homeomorficzne z jednowymiarową przestrzenią euklidesową)[b]
- dwuwymiarowe: płaszczyzna, sfera, torus i inne powierzchnie; wszystkie te powierzchnie mogą być zanurzone w trójwymiarowej przestrzeni euklidesowej bez spowodowania przecinania się powierzchni samej ze sobą; także butelka Kleina oraz płaszczyzna rzutowa rzeczywista, które będą przecinać się ze sobą, gdy zanurzy się je w trójwymiarowej przestrzeni euklidesowej
- wielowymiarowe, np. hiperpowierzchnie w przestrzeni euklidesowej n-wymiarowej (czyli przestrzenie o wymiarze n-1).
Rozmaitości przypominają przestrzeń euklidesową w otoczeniu każdego punktu (lokalnie), ale ich globalna struktura może być bardziej skomplikowana. Przykładowo otoczenie dowolnego punktu sfery jest homeomorficzne z płaszczyzną, gdyż można je przekształcić na płaską mapę (co realizuje się np. wykonując mapy geograficzne). Jednakże sfera różni się od płaszczyzny w „wielkiej skali”. Dlatego do odwzorowania sfery na płaszczyznę potrzeba większej liczby map. Mapy te tworzą atlas, analogicznie do atlasu zawierającego mapy geograficzne Ziemi. W ogólnym przypadku rozmaitości lokalnie mają własności przestrzeni euklidesowych wymiaru n (n = 1, 2, 3, 4 itd.), dlatego ich odwzorowanie na przestrzeń euklidesową wymaga map n-wymiarowych.
Koncepcja rozmaitości jest kluczowa w wielu gałęziach geometrii i nowoczesnej fizyki matematycznej, ponieważ umożliwia opisanie i rozumienie skomplikowanych struktur za pomocą dobrze poznanych właściwości przestrzeni euklidesowych. Rozmaitości pojawiają się w sposób naturalny jako rozwiązania układów równań oraz jako wykresy funkcji[c].
Rozmaitości mogą posiadać dodatkowe własności:
- Rozmaitości różniczkowe – rozmaitości posiadające lokalne układy współrzędnych, zadane za pomocą funkcji -krotnie różniczkowalnych (gdzie ), co umożliwia np. wykonywanie na nich różnego rodzaju różniczkowań i całkowań.
- Rozmaitości riemannowskie – rozmaitości różniczkowe uzupełnione o metrykę Riemanna, co pozwala mierzyć na nich odległości i kąty.
- Rozmaitości symplektyczne – służą jako przestrzenie fazowe mechaniki klasycznej wyrażonej w formalizmie Hamiltona.
- Czterowymiarowe rozmaitości lorentzowskie – są modelami czasoprzestrzeni w ogólnej teorii grawitacji.
Historia[edytuj | edytuj kod]
Badanie rozmaitości łączy wiele ważnych dziedzin matematyki. Pojęcie rozmaitości uogólnia pojęcia krzywej i powierzchni na przestrzenie wielowymiarowe.
Wczesny rozwój[edytuj | edytuj kod]
Zanim powstało nowoczesne pojęcie rozmaitości, osiągnięto już kilka wyników.
Geometrie nieeuklidesowe[edytuj | edytuj kod]
Geometria nieeuklidesowa opisuje przestrzenie, gdzie nie obowiązuje piąty aksjomat Euklidesa. Szczegółowe badania tej geometrii rozpoczął Saccheri w 1733 roku. Łobaczewski, Bolyai i Riemann rozwijali je 100 lat później. Ich badania doprowadziły do odkrycia dwóch nowych rodzajów przestrzeni, w których obowiązują geometrie inne od euklidesowej – hiperboliczna i eliptyczna. Dlatego przestrzenie te różnią się od klasycznej przestrzeni euklidesowej. W nowoczesnej teorii rozmaitości określa się je jako rozmaitości riemannowskie odpowiednio o stałej ujemnej i stałej dodatniej krzywiźnie.
Krzywizna powierzchni – własność wewnętrzna[edytuj | edytuj kod]
Carl Friedrich Gauss był prawdopodobnie pierwszym matematykiem, który rozważał abstrakcyjne przestrzenie jako obiekty matematyczne. Jego twierdzenie Theorema Egregium stwierdza, że krzywizna powierzchni jest jej wewnętrzną własnością, bo można ją obliczyć, nie odwołując się do własności przestrzeni, w której powierzchnia jest zanurzona. Powierzchnie o własnościach zakładanych przez Gaussa nazywamy rozmaitościami.
Teoria rozmaitości skupiła swoje badania na odkrywaniu własności wewnętrznych (niezmienników), w zasadzie pomijając właściwości zewnętrznej przestrzeni.

Charakterystyka Eulera – własność topologiczna[edytuj | edytuj kod]
Innym, topologicznym przykładem wewnętrznej własności rozmaitości jest charakterystyka Eulera. Leonhard Euler wykazał najpierw, że dla wypukłego wielościanu (czyli wielokomórki w trójwymiarowej przestrzeni euklidesowej) słuszna jest zależność
gdzie:
- – liczba wierzchołków,
- – liczba krawędzi,
- – liczba ścian.
Następnie pokazał, że reguła ta pozostanie słuszna, jeśli dokona się rzutu wierzchołków i krawędzi na sferę, tworząc mapę topologiczną. Wynika z tego, że liczba 2 jest niezmiennikiem sfery, zwanym jej charakterystyką Eulera.
(Ten sam wynik uzyska się, jeśli dokona się podziału powierzchni za pomocą dowolnych linii w niej zawartych, które przecinają się. Np. dzieląc sferę za pomocą południka i równoleżnika, otrzyma się W = 2 wierzchołki, K = 4 krawędzie i S = 4 ściany; charakterystyka Eulera dla sfery wynosi więc 2.)
Inaczej jest na torusie: dzieląc jego powierzchnię za pomocą jednego równoleżnika i jednego południka otrzyma się W = 1 wierzchołek, K = 2 krawędzie i S = 1 ścianą[d]; charakterystyka Eulera dla torusa wynosi więc 0 (bo 1 – 2 + 1 = 0).
Charakterystyka Eulera stanowi niezmiennik topologiczny danej powierzchni, tzn. deformacja powierzchni za pomocą np. ciągłego rozciągania (bez rozrywania) zachowuje ten niezmiennik[e].
Charakterystyka Eulera może być uogólniona na rozmaitości topologiczne o wyższych wymiarach.
Synteza[edytuj | edytuj kod]
Niels Henrik Abel i Carl Gustav Jakob Jacobi, prowadząc badania nad odwrotnością całek eliptycznych w pierwszej połowie XIX wieku, doszli do rozważań nad szczególnymi rozmaitościami zespolonymi, zwanymi dzisiaj Jacobianami. Bernhard Riemann uzupełnił ich teorię, wyjaśniając znaczenie przedłużenia analitycznego funkcji zmiennej zespolonej.
Innym ważnym źródłem rozwoju idei rozmaitości w matematyce XIX wieku była mechanika analityczna – wersja mechaniki klasycznej rozwinięta przez Siméon Poissonna, Jacobiego i Williama Hamiltona. Możliwe stany układu mechanicznego zostały zdefiniowane tam jako punkty w abstrakcyjnej przestrzeni, przestrzeni fazowej, której wymiar jest równy liczbie stopni swobody układu, a punkty są zadane przez współrzędne uogólnione. Przestrzeń fazowa jest w ogólnym przypadku wielowymiarową rozmaitością. Jedynie w przypadku ruchu cząstek swobodnych (tj. nie poddanych działaniu więzów) rozmaitość sprowadza się do przestrzeni euklidesowej.
Riemann jako pierwszy wykonał wiele prac nad uogólnieniem pojęcia powierzchni w wyższych wymiarach. Nazwa rozmaitość pochodzi od pierwotnej niemieckiej nazwy Mannigfaltigkeit, wymyślonej przez Riemanna i oznaczającej różnorodność. W swoim wykładzie inauguracyjnym w Getyndze Riemann opisał zbiór wszystkich możliwych wartości zmiennej z pewnymi ograniczeniami jako Mannigfaltigkeit, ponieważ zmienna może mieć wiele wartości. Jako przykłady wartości Riemann podawał nie tylko kolor czy położenie w przestrzeni, ale także wszystkie możliwe kształty. Korzystając z indukcji, dokonał konstrukcji rozmaitości n-wymiarowych jako stos rozmaitości (n -1)- wymiarowych.
Hermann Weyl podał szczegółową definicję rozmaitości różniczkowalnych, otwierając drogę do ogólnego pojęcia przestrzeni topologicznej.
Przykłady rozmaitości[edytuj | edytuj kod]
Krzywe[edytuj | edytuj kod]
Okrąg[edytuj | edytuj kod]

Po linii okrąg jest najprostszym przykładem rozmaitości topologicznej. W topologii wygięcie nie ma znaczenia, mały fragment okręgu jest traktowany tak samo jak mały fragment linii. Np. dla okręgu jednostkowego, x2 + y2 = 1 (ilustracja 1) rozważmy jego fragment - zbiór otwarty punktów tworzący łuk koloru żółtego. Każdy jego punkt może być jednoznacznie opisany za pomocą współrzędnej x (współrzędne y punktów są tu dodatnie). Wynika stąd, że rzut żółtego fragmentu okręgu na otwarty przedział (–1, 1) na osi x jest ciągły i odwracalny,
Rzut ten nazywa się mapą żółtego fragmentu.
Ogólnie, mapą nazywa się funkcję, która odwzorowuje wzajemnie jednoznacznie otwarty przedział danej przestrzeni na przestrzeń euklidesową (ściśle: mapa powinna być homeomorfizmem).
Podobnie tworzymy mapy dla pozostałych fragmentów okręgu: dolny (czerwony), lewy (niebieski) i prawy (zielony). Wszystkie te fragmenty obejmują cały okrąg, a cztery mapy tworzą atlas dla okręgu.
Górna i prawa mapa się nakładają: ich część wspólna leży w części okręgu, gdzie obie współrzędne x i y są dodatnie. Obie te mapy χgórny i χprawy odwzorowują tę część w przedział (0, 1). Stąd można utworzyć funkcję T z (0, 1) na siebie, gdzie najpierw odwrócimy przedział górny na okrąg, a następnie za pomocą prawej mapy wrócimy na ten sam przedział. Niech a będzie dowolną liczbą z przedziału (0, 1), wtedy:
Taką funkcję nazywamy przekształceniem przejścia.
Para oddzielnych okręgów[edytuj | edytuj kod]
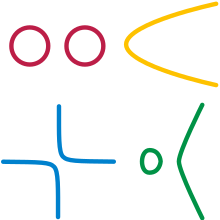
Rozmaitości nie muszą być spójne (całe w „jednym kawałku”). Prosty przykład stanowi para oddzielnych okręgów. W tym przypadku widać, że rozmaitość nie musi mieć dobrze zdefiniowanego pojęcia odległości, gdyż nie ma sposobu na zdefiniowanie odległości między punktami, które leżą na różnych okręgach.
Dwa styczne okręgi[edytuj | edytuj kod]
Przypadek trudnej rozmaitości to dwa styczne okręgi, tworzące kształt cyfry 8. Punkt styczności uniemożliwia utworzenie zadowalającej mapy. Nawet jeśli wyginanie jest dozwolone w topologii, okolice punktu styczności przypominają znak „+”, a nie linię. Kształt „+” nie jest homeomorficzny z odcinkiem, gdyż usunięcie środkowego punktu utworzy przestrzeń czteroelementową, podczas gdy dzielenie odcinka daje w wyniku co najwyżej przestrzeń dwuelementową. Przekształcenia topologiczne zawsze zachowują liczbę elementów.
Wzbogacony okrąg[edytuj | edytuj kod]
Przekształcenie przejścia T dla okręgu to prosta funkcja pomiędzy otwartymi przedziałami. Łatwo zauważyć, że można wobec niej zastosować rachunek różniczkowy i całkowy na przedziale (0, 1), dlatego z tego atlasu wynika, że okrąg to rozmaitość różniczkowalna. Ponadto jest też gładki i analityczny, gdyż przekształcenie przejścia ma także te własności.
Inne właściwości okręgu pozwalają zaliczyć go do bardziej szczególnych rozmaitości. Np. istnieje pojęcie odległości między dwoma punktami na okręgu (zdefiniowane poprzez długości łuku łączącego te punkty), dlatego okrąg jest rozmaitością riemannowską.
Powierzchnie[edytuj | edytuj kod]
Zobacz też[edytuj | edytuj kod]
- rozmaitość w teorii algebr uniwersalnych
- rozmaitość abelowa
- rozmaitość algebraiczna
- rozmaitość kombinatoryczna
- rozmaitość liniowa
- rozmaitość pseudoriemannowska
- rozmaitość riemannowska
- rozmaitość różniczkowa
- rozmaitość symplektyczna
- rozmaitość topologiczna
Uwagi[edytuj | edytuj kod]
- ↑ Intuicyjnie, dwie przestrzenie są homeomorficzne jeżeli jedną z nich można przekształcić w drugą przez ściskanie, rozciąganie, wyginanie lub skręcanie, ale bez rozrywania, sklejania jej fragmentów czy robienia w niej dziur.
- ↑ Krzywe te są przykładami przestrzeni topologicznych, które stanowią struktury o własnościach mniej restrykcyjnych niż rozmaitości.
- ↑ Wykresy funkcji są krzywymi, które nie przecinają się ze sobą, dlatego spełniają kryteria wymagane od rozmaitości: otoczenie każdego punktu można przekształcić homeomorficznie na przestrzeń euklidesową 1-wymiarową; są to więc rozmaitości 1-wymiarowe.
- ↑ Warto to sprawdzić wykonując osobiście prosty eksperyment, np. rysując linie na zwiniętej w pierścień tasiemce papieru.
- ↑ Łatwo to sprawdzić – np. rysując linie na piłeczce pingpongowej czy jajku otrzymamy zawsze charakterystykę Eulera równą 2.
Przypisy[edytuj | edytuj kod]
- ↑ Rozmaitość, [w:] Encyklopedia PWN [dostęp 2021-08-07].









![{\displaystyle {\begin{aligned}T(a)&=\chi _{\mathrm {prawy} }\left(\chi _{\mathrm {g{\acute {o}}rny} }^{-1}[a]\right)\\&=\chi _{\mathrm {prawy} }\left(a,{\sqrt {1-a^{2}}}\right)\\&={\sqrt {1-a^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9365126836644aeb6043aebd15ee8111f4b3cd5c)