Topologia



Topologia (gr. τόπος (tópos), miejsce, okolica; λόγος (lógos), słowo, nauka) – dział matematyki wyższej zajmujący się badaniem przestrzeni topologicznych, czyli najogólniejszych przestrzeni, dla których można zdefiniować pojęcie przekształcenia ciągłego[1]. Topologia bada zwłaszcza własności zachowywane przez homeomorfizmy – np. orientowalność powierzchni, genus („liczbę otworów”), istnienie (niepustego) brzegu i jego podstawowe cechy. Właściwości tego typu są nazywane niezmiennikami topologicznymi[1].
Nieformalnie mawia się, że własności topologiczne nie ulegają zmianie nawet po radykalnym zdeformowaniu obiektów, np. figur geometrycznych jak bryły i ich odpowiedniki o innej liczbie wymiarów. Przez deformowanie rozumie się tutaj dowolne odkształcanie – jak zginanie, rozciąganie czy skręcanie – ale bez rozrywania różnych części lub zlepiania różnych punktów[2]. Proces deformacji można wyobrazić sobie, przyjmując, że obiekt wykonano z gumy[3]. Pod tym kątem można analizować między innymi obiekty geometryczne jak przestrzenie euklidesowe, inne rozmaitości i ich podzbiory, a topologia wyrosła właśnie z geometrii i bywała określana jako teoria umiejscowienia (łac. analysis situs)[1]. Mimo to w ogólności nie posługuje się ona pojęciami ilościowymi jak odległość czy miara kąta; nie uwzględnia nawet niektórych jakościowych relacji geometrycznych jak równoległość prostych[1]. Taki minimalizm umożliwił uściślenie pojęć o geometrycznym rodowodzie jak krzywa czy abstrakcyjny wymiar zbioru, bez odwoływania się do algebry liniowej czy teorii miary. Topologia wkroczyła też w różne dziedziny matematyki odległe od jej korzeni. Przykładem jest analiza funkcjonalna[1] – intuicyjne pojęcie spójności można uogólnić m.in. na przestrzenie funkcyjne jak te Hilberta, Banacha czy jeszcze ogólniejsze przestrzenie liniowo-topologiczne, które stały się definiującym tematem tego działu matematyki. Metody topologiczne zastosowano nawet w teorii liczb[4][5].
Geneza topologii, zwłaszcza rozumianej potocznie, bywa wiązana z XVIII-wiecznymi początkami teorii grafów w pracach Leonharda Eulera. Mimo to topologia sensu stricto wyrosła w II połowie XIX wieku, na pograniczu geometrii, analizy i teorii mnogości. Została nazwana przez Johanna Listinga w 1847 roku[1], a ogólny obszar badań tej dziedziny – czyli przestrzeń topologiczną – zdefniowano na początku XX wieku, w pracach Feliksa Hausdorffa i Kazimierza Kuratowskiego[6]. Od tego czasu wykształciły się całe zróżnicowane gałęzie tej nauki – oprócz topologii ogólnej i mnogościowej powstały między innymi topologia algebraiczna, różniczkowa i geometryczna[7]. Badają one różne szczególne klasy przestrzeni topologicznych, niezmienniki specjalnych typów homeomorfizmów – jak np. dyfeomorfizmy – i czerpią przy tym z różnych działów matematyki, zwłaszcza teorii grup. Osobną, owocną dyscypliną stała się też teoria węzłów, bliska korzeniom topologii w jakościowej stereometrii (trójwymiarowej geometrii euklidesowej). Topologia była jednym z głównych obszarów badań warszawskiej szkoły matematycznej, a osiągnięcia Polaków w tej dziedzinie upamiętniono m.in. nazwą przestrzeni polskiej. Prace Samuela Eilenberga w topologii algebraicznej przyczyniły się do powstania teorii kategorii; wiązanej głównie z algebrą i odgrywającej dużą rolę w różnych obszarach matematyki oraz poza nią.
Pytania postawione przez topologię uznano za doniosłe. W 2000 roku hipotezę Poincarégo w topologii algebraicznej umieszczono na liście siedmiu problemów milenijnych, a rozwiązanie jej przez Grigorija Perelmana nagrodzono dodatkowo (odrzuconym przez laureata) Medalem Fieldsa[a]. Już wcześniej odznaczano tym medalem badania nad tą hipotezą, m.in. przez Stephena Smale’a, Michaela Freedmana i Williama Thurstona. Wybitne postępy w topologii nagradzano też innymi najwyższymi zaszczytami dostępnymi matematykom jak Nagroda Abela i Medal Copleya. Topologia wywiera też bezpośredni wpływ na rozmaite kierunki fizyki teoretycznej – teorię cząstek elementarnych (np. teorię strun), informatykę kwantową[9], biofizykę molekularną czy fizykę materii skondensowanej; przykładowo była wprost wspomniana w uzasadnieniu Nagrody Nobla w dziedzinie fizyki za 2016 rok[b]. Pojęcia i wyniki topologiczne mają też znaczenie dla kosmologii – otwartym pozostaje pytanie o kształt Wszechświata; rozważano modele o różnych, czasem nietrywialnych ułożeniach czasoprzestrzeni[10].
Rys historyczny[edytuj | edytuj kod]
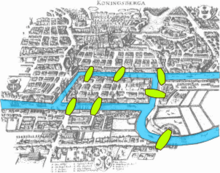

Przez Królewiec przepływa rzeka Pregoła, dzieląc miasto na dwie części; na niej dodatkowo znajdują się dwie wyspy (Knipawa i Lomse), co pokazuje ilustracja obok. Zastanawiano się, czy możliwe jest przejście przez wszystkie mosty królewieckie, pokonując każdy z nich co najwyżej raz[11][12][13].
W postawionym problemie nieważne są odległości między mostami, ich długości, współliniowość punktów ani kąty. Zagadnienie mostów królewieckich rozwiązał w 1736 roku Leonhard Euler, który wykazał, że jest to niemożliwe[13].
Podobnie topologiczny charakter ma twierdzenie Eulera o wielościanach wypukłych, które mówi, że suma liczby wierzchołków takiego wielościanu oraz liczby jego ścian równa jest liczbie krawędzi powiększonej o dwa. Wynik nie zależy od długości krawędzi czy kątów (poza wypukłością). Dziś o tym twierdzeniu mówi się jako o twierdzeniu o sferze dwuwymiarowej, uogólnionym przez Henriego Poincaré na dowolne wielościany, a przez Solomona Lefschetza na odwzorowania ciągłe wielościanów w siebie.
Wspomniane historycznie pierwsze wyniki topologiczne zostały uzyskane na długo przed ustanowieniem topologii jako osobnego działu matematyki, dlatego powszechnie uważa się Eulera za jej prekursora. Twierdzenia te mają charakter kombinatoryczny, z tego też powodu poprzedniczkę dzisiejszej topologii algebraicznej nazywano niegdyś topologią kombinatoryczną.
Nieco inny charakter ma klasyczne twierdzenie Weierstrassa analizy: każda funkcja ciągła rzeczywista zdefiniowana na odcinku domkniętym jest ograniczona i osiąga swoje kresy. Podobnie jak w przypadku twierdzeń Eulera, wspomniane zdanie ma wymiar geometryczny, gdyż mówi o geometrycznych własnościach wykresów, ale różni się zasadniczo od twierdzeń geometrii klasycznej – takich jak na przykład twierdzenie Pitagorasa: w geometrii liczą się miary kątów, boków, powierzchni, ich proporcje oraz to, czy dane punkty leżą na jednej prostej, krzywej lub płaszczyźnie. Wszystkie te zagadnienia nie mają znaczenia w powyższych przykładach twierdzeń topologicznych.
Za twórcę topologii uważa się Bernharda Riemanna, który jako pierwszy prowadził badania stricte topologiczne, choć pewne wyniki, które dziś zaliczamy do topologii, znane były już wcześniej.
Jako osobna dziedzina matematyki topologia zaczęła się rozwijać u progu XX wieku, a przez kolejne 50 lat była najbujniej rozwijającą się dziedziną matematyki, w czym niemały udział mieli matematycy skupieni w polskiej szkole matematycznej. W początkowym okresie rozwoju topologii matematycy określali nową dziedzinę jako geometria situs (łac. geometria położenia/miejsca) lub analysis situs (łac. analiza położenia/miejsca).
Termin „topologia” został po raz pierwszy użyty w druku przez niemieckiego matematyka Johanna Benedicta Listinga w 1847[14], a około roku 1920 uznano powstanie nowej dziedziny matematyki. Matematyków zajmujących się topologią zaczęto nazywać topologami.
Jednymi z najważniejszych wydarzeń w historii topologii są:
- W 1854 Riemann wygłasza na uniwersytecie w Getyndze wykład habilitacyjny O hipotezach, jakie leżą u podstaw geometrii[15] w którym wprowadził podstawy geometrii Riemanna.
- W końcu XIX w. Georg Cantor zainteresowany podzbiorami prostej rzeczywistej pojawiającymi się w teorii szeregów Fouriera rozwinął podstawy teorii mnogości. Rozważał on otwarte i domknięte podzbiory przestrzeni euklidesowych, a także operacje wnętrza i domknięcia w tych przestrzeniach. Wkrótce jego prace stały się podstawą wszelkich badań w topologii ogólnej.
- W 1890 Giuseppe Peano podał przykład ciągłego odwzorowania z odcinka na kwadrat Ten i inne przykłady krzywych Peana były bodźcem do rozwoju teorii wymiaru.
- W 1894 Henri Poincaré wprowadził pojęcie grupy podstawowej i pokazał, że dwuwymiarowa powierzchnia zwarta (bez brzegu), o trywialnej grupie podstawowej, jest homeomorficzna z dwuwymiarową sferą. Następnie próbował, bez sukcesu, dowieść analogicznej hipotezy, zwanej hipotezą Poincarego, dla rozmaitości trójwymiarowych. Udało się to dopiero Grigorijowi Perelmanowi.
- W 1895 Henri Poincaré opublikował pracę Analysis Situs[16], w której wprowadził pojęcia homotopii i liczb Bettiego, które Emma Noether zastąpiła grupami homologii, i dał pierwsze systematyczne podejście do topologii, ustalając podstawy topologii algebraicznej.
- W 1906 Maurice Fréchet w swojej rozprawie doktorskiej[17] wprowadził pojęcie przestrzeni metrycznej (chociaż sam nie używał tej nazwy, a została ona nadana tego typu przestrzeniom później przez Felixa Hausdorffa). Fréchet rozważał też abstrakcyjne struktury topologiczne zdefiniowane w terminach ciągów zbieżnych (co jest odzwierciedlone we współczesnej terminologii przez pojęcie przestrzeni Frécheta).
- W 1914 r. Felix Hausdorff wprowadził pojęcie przestrzeni topologicznej, a podana przez niego definicja obejmuje szeroką klasę przestrzeni znanych dzisiaj jako przestrzenie Hausdorffa (aksjomaty Hausdorff w zasadzie zaadaptował z wcześniejszych badań Hilberta, dotyczących szczególniejszej sytuacji z geometrii klasycznej).
- Definicję przestrzeni topologicznej w terminach operacji domknięcia, równoważną z dziś powszechnie stosowaną, sformułował Kazimierz Kuratowski[18]. Początkowo jego definicja obejmowała przestrzenie T1.
Podstawowe pojęcia[edytuj | edytuj kod]
Zbiory otwarte[edytuj | edytuj kod]
Korzenie topologii tkwią w geometrii i często mówi się o topologii jako o jednej z geometrycznych dziedzin matematyki. Z drugiej strony, topologia ogólna wyrosła z analizy matematycznej. Zarówno w geometrii, jak i w analizie ważnym pojęciem jest odległość. Odległość można zdefiniować na wiele sposobów w przestrzeni euklidesowej, jak i w innych przestrzeniach. Zbiór ze zdefiniowaną odległością (tzw. metryką) jest zwany przestrzenią metryczną.
Zauważono jednak, że wiele własności obiektów studiowanych w analizie może być scharakteryzowanych przy użyciu jedynie zbiorów otwartych bez potrzeby odwoływania się do pojęcia metryki. Zbiory otwarte w przestrzeni metrycznej to takie zbiory, które są sumami (również nieskończonymi) kul otwartych, a więc zbiorów punktów odległych od zadanego punktu (środka) o mniej niż zadana odległość (promień). Często okazuje się, że poznanie struktury zbiorów otwartych jest bardziej użyteczne niż badanie przestrzeni za pomocą metryki.
- Przykład
- Zbiorem otwartym na płaszczyźnie jest np. wnętrze dowolnego spójnego wielokąta. Można je skonstruować jako sumę nieprzeliczalnego zbioru kul otwartych, wypełniających wielokąt.
Otoczenia[edytuj | edytuj kod]

Otoczenia to zbiory spełniające następujące warunki:
- Dla każdego punktu istnieje jakieś jego otoczenie, a każde otoczenie zawiera pewien punkt.
- Jeśli punkt należy do otoczenia punktu to istnieje takie otoczenie punktu które zawiera się w – intuicyjnie: skoro w pewnym sensie leży blisko to istnieją punkty leżące w pobliżu zarówno jak i
- Dla dowolnych dwóch otoczeń punktu istnieje otoczenie tego punktu, które się w nich zawiera.
Niektórzy autorzy do definicji dodają warunek, iż otoczenie musi być zbiorem otwartym.
Otoczenie punktu można sobie wyobrazić jako dowolną figurę, wewnątrz której znajduje się punkt Każdy punkt przestrzeni euklidesowej posiada nieskończenie wiele otoczeń, z których niektóre zawierają się w innych. To zawieranie się otoczeń jest jedynym odpowiednikiem informacji o odległości danych punktów. Z drugiej strony otoczenia zostają zachowane przy homeomorficznych przekształceniach przestrzeni, co sprawia, że są w topologii użytecznym narzędziem.
Mając dany zbiór punktów i bazę ich otoczeń, możemy wygenerować przestrzeń topologiczną – wystarczy za zbiór otwarty uznać zbiór dla którego nie istnieją punkty brzegowe, czyli takie, których wszystkie otoczenia zawierają zarówno punkty ze zbioru jak i spoza tego zbioru (patrz rysunek obok).
Przestrzeń topologiczna[edytuj | edytuj kod]
Topologią na zbiorze nazywa się dowolną rodzinę podzbiorów spełniającą następujące warunki:
- zbiór pusty oraz należą do
- suma dowolnej rodziny zbiorów z należy oraz
- jeżeli to również
Elementy tej rodziny nazywane są zbiorami otwartymi w ich dopełnienia nazywane są zbiorami domkniętymi, a parę nazywa się przestrzenią topologiczną.
W danej przestrzeni można na ogół utworzyć wiele różnych topologii. Jeżeli topologię w można utworzyć, posługując się jakąś metryką, to o przestrzeni mówi się, że jest metryzowalna. Np. metryzowalne są przestrzenie euklidesowe (prosta rzeczywista, płaszczyzna, przestrzeń trójwymiarowa itd.). Badane w topologii własności są uogólnieniami własności znanych z tychże przestrzeni.
Istnieją również przestrzenie topologiczne niemetryzowalne (np. iloczyn kartezjański nieprzeliczalnej rodziny co najmniej dwupunktowych przestrzeni topologicznych z topologią Tichonowa), dlatego też pojęcie przestrzeni topologicznej jest uogólnieniem pojęcia przestrzeni metrycznej.
Homeomorfizm[edytuj | edytuj kod]
Pewne wyobrażenie o tym, czym zajmuje się topologia przestrzeni euklidesowych, można sobie wyrobić, jeżeli przywoła się przed oczy obraz zbiorów wykonanych z gumy. Z punktu widzenia topologii interesujące jest np. to, że węzeł (pokazany na rysunku obok) nie daje się bez rozcinania sprowadzić do euklidesowego okręgu, nie jest natomiast ważne, jakie ten węzeł ma rozmiary i krzywiznę „pętelek”, co byłoby istotne w geometrii.
Formalnie dwie przestrzenie są homeomorficzne, jeśli istnieje ciągła bijekcja z jednej z nich na drugą, której odwrotność też jest ciągła.
Gdy przestrzeń X daje się homeomorficznie odwzorować na przestrzeń Y, to przestrzenie X i Y mają takie same własności topologiczne i z punktu widzenia topologii są nieodróżnialne (homeomorficzne), mogą być traktowane jako różne egzemplarze tej samej przestrzeni. Przykładami własności topologicznych zachowywanych przez homeomorfizm są spójność („składanie się z jednego kawałka”) i wymiar (topologiczny) przestrzeni.

- Przykład
- Topologa określa się żartobliwie jako matematyka, który nie potrafi odróżnić kubka do kawy od obwarzanka. Istotnie, animacja załączona obok pokazuje sposób deformacji kubka do postaci obwarzanka i odwrotnie. Co ważne, deformacja przebiega w sposób ciągły, czyli bez rozrywania i sklejania, co oznacza właśnie, iż kubek i obwarzanek są homeomorficzne, a więc z punktu widzenia topologii nieodróżnialne.
Nietrudno teraz podać inne przykłady przestrzeni, które dla topologa niczym się nie różnią. Kulka plasteliny jest tym samym, co ulepiona z niej żyrafa (o ile podczas jej lepienia nie rozerwiemy i nie skleimy ze sobą wygiętych i rozciągniętych kawałków), trójkąt jest tym samym co kwadrat (a nawet koło).
Gałęzie topologii[edytuj | edytuj kod]
Zgodnie z klasyfikacją badań naukowych w matematyce prowadzoną przez Amerykańskie Towarzystwo Matematyczne, współczesne badania topologiczne są podzielone na trzy poddziały.
Topologia ogólna (54xx)[edytuj | edytuj kod]
Obiektem badań tutaj są przestrzenie topologiczne w swojej najogólniejszej postaci[19], ale często również wyposażone w dodatkową strukturę (np. metrykę) lub posiadające dodatkowe własności (np. bada się przestrzenie zwarte). Typowe tematy rozważań w topologii ogólnej to np. aksjomaty oddzielania, zachowywanie różnych własności w iloczynach przestrzeni topologicznych czy też przez ciągłe obrazy, własności pierścienia funkcji ciągłych na danej przestrzeni, uzwarcenia przestrzeni topologicznych czy też funkcje kardynalne. Korzysta się tu często z metod teorii mnogości i nierzadko można spotkać twierdzenia zakładające aksjomat Martina, PFA czy wyniki forsingowe dotyczące niezależności pewnych stwierdzeń od aksjomatów ZFC.
Topologia algebraiczna (55xx)[edytuj | edytuj kod]
- Z przestrzeniami topologicznymi wiąże się różne obiekty algebraiczne (przykładem może być tzw. grupa podstawowa). Ponieważ obiektom izomorficznym w sensie topologicznym (czyli homeomorficznym) przyporządkowuje się obiekty izomorficzne w sensie algebraicznym, to badając uzyskane struktury algebraiczne, można poznać własności danych przestrzeni topologicznych.
Topologia rozmaitości (57xx)[edytuj | edytuj kod]
- Rozmaitości to przestrzenie topologiczne, które „lokalnie” wyglądają tak jak przestrzenie euklidesowe. Często wyposażone są one w strukturę różniczkową lub kawałkami liniową. Są to zwykle najbardziej „naturalne” przykłady przestrzeni topologicznych, włączając w to dobrze znane powierzchnie. Nierzadko do badania tych obiektów używa się metod topologii algebraicznej.
Poddziałami topologii rozmaitości są:
Topologia różniczkowa (57Rxx)[edytuj | edytuj kod]
Topologia różniczkowa zakłada o rozmaitościach topologicznych, że mają również strukturę różniczkową. W dziale tym stosuje zatem metody różniczkowe analizy matematycznej, w szczególności teorię Morse’a. Za początek topologii różniczkowej przyjmuje się odkrycie przez Johna Milnora niedyfeomorficznych struktur różniczkowych na siedmiowymiarowej sferze.
- Podstawowym narzędziem topologii różniczkowej jest między innymi twierdzenie Sarda, które mówi, że miara Lebesgue’a zbioru punktów krytycznych odwzorowania rzeczywistego, gładkiego podzbioru otwartego -wymiarowej przestrzeni euklidesowej wynosi zero.
Teoria węzłów (57M25, 57M27, 57M30)[edytuj | edytuj kod]

- Szczególną gałęzią topologii rozmaitości jest teoria węzłów, która zajmuje się krzywymi zwykłymi zamkniętymi, zanurzonymi w przestrzeni trójwymiarowej. O ile w przestrzeniach dwuwymiarowych, a także cztero- i więcej wymiarowych każda taka krzywa daje się bez rozcinania przekształcić w okrąg, to w przestrzeni trójwymiarowej istnieje nieskończona liczba takich nierównoważnych krzywych, zwanych węzłami. Najprostszy z nich (oprócz trywialnego okręgu) to koniczynka, pokazana wyżej.
- Teoria węzłów zajmuje się też położeniem w trójwymiarowej przestrzeni euklidesowej skończonych układów krzywych zamkniętych, badając przy tym sposób ich zaczepienia. Oprócz wspomnianych węzłów jednowymiarowych, rozwijana jest także teoria węzłów wielowymiarowych,
Poza wymienionymi wyżej trzema głównymi działami topologii wyróżnia się także:
Topologiczna teoria wymiaru[edytuj | edytuj kod]
- Teoria wymiaru topologicznego znajduje się na granicy topologii ogólnej i algebraicznej.
- Kiedy Peano odkrył odwzorowanie ciągłe odcinka domkniętego na kwadrat, powstało niepokojące pytanie, czy topologia w ogóle jest w stanie rozróżnić wyżej wymiarowe przestrzenie euklidesowe, czy przypadkiem przestrzenie cztero- i pięciowymiarowe nie są homeomorficzne. Problem ten rozstrzygnął Brouwer, dowodząc niehomeomorficzności przestrzeni euklidesowych o różnym wymiarze. Brouwer był jednym z głównych prekursorów topologicznej teorii wymiaru, stworzonej przez Urysohna i Mengera.
- Teoria wymiaru przypisuje przestrzeniom topologicznym liczbę całkowitą ≥ -1. Istnieje więcej niż jedno pojęcie wymiaru, są to m.in. klasyczne funkcje dim, ind i Ind oraz pewne algebraicznie subtelne definicje. Jednak wszystkie te funkcje przypisują wymiar równy -1 tylko i wyłącznie przestrzeni pustej, z kolei wymiar zerowy mają wszystkie przestrzenie dyskretne, ale nie tylko one. Wszystkie trzy powyższe funkcje klasyczne pokrywają się w zakresie przestrzeni polskich (czyli metrycznych, ośrodkowych).
- Nawet w tym ograniczonym zakresie wymiar topologiczny różni się cechami od algebraicznego lub geometrycznego. W przypadku przestrzeni liniowych lub zbiorów i rozmaitości algebraicznych, podobnie jak w przypadku wielościanów, wymiar ma własność logarytmiczną: wymiar iloczynu kartezjańskiego jest równy sumie wymiarów czynników. Topologia, nawet przestrzeni polskich, zajmuje się znacznie bogatszą rodziną obiektów i prawo logarytmiczne w topologii nie zachodzi, co pokazuje piękny przykład pochodzący od Erdősa:
- Przestrzeń wszystkich punktów klasycznej przestrzeni Hilberta o samych wymiernych współrzędnych, jest jednowymiarowa, a jej kwadrat jest homeomorficzny z nią samą. Zgodnie z prawem logarytmicznym druga przestrzeń powinna mieć wymiar 1+1, ale ma wymiar 1. Trudniej o takie przykłady w przypadku zwartych przestrzeni metrycznych. Ich wymiar dim musi wynosić co najmniej dwa. Przykład dwóch przestrzeni o wymiarze dwa, ale wymiarze ich iloczynu wynoszącym trzy podał Pontriagin, a Bołtiański[20] skonstruował taką zwartą, dwuwymiarową przestrzeń metryczną, której kwadrat wynosi trzy. Prawo logarytmiczne jest jednym z szeregu problemów teorii wymiaru.
- Topologiczna teoria wymiaru jest (w dużej mierze) zawarta w teorii funkcji uniwersalnych[21] (patrz Morfizm uniwersalny):
- Twierdzenie[21]: wtedy i tylko wtedy, gdy istnieje funkcja uniwersalna (dla dowolnej przestrzeni całkowicie regularnej).
Pierwszą monografią poświęconą topologicznej teorii wymiaru jest klasyczna książka autorstwa Witolda Hurewicza i Henry’ego Wallmana pt. Dimension Theory.
Topologia nieskończeniewymiarowa[edytuj | edytuj kod]
Wielu matematyków miało istotny wkład do topologii nieskończeniewymiarowej; wśród głównych pionierów należy wymienić Richarda Andersona. Głównych twórców, ze względu na rozmach i kompletność wyników, jest czterech (alfabetycznie): Thomas Chapman, Robert Edwards (matematyk), Henryk Toruńczyk oraz James West. Przy tym metody i prace Toruńczyka są szczególnie eleganckie.
U podstawy teorii legły dwa, dopiero po latach rozwiązane pytania:
- Czy wszystkie nieskończeniewymiarowe ośrodkowe przestrzenie Banacha są homeomorficzne?
- Czy iloczyn topologiczny przestrzeni z kostką Hilberta jest homeomorficzny z kostką Hilberta?
Drugie pytanie wymyślił i wpisał Karol Borsuk do Księgi szkockiej. O odpowiedzi-rozwiązaniu przez kolegów matematyków James West poinformował uczestników konferencji w Baton Rouge (Louisiana State University), tak określając dwa niezależne dowody: Anderson – terrible argument; Andrzej Szankowski – beautiful argument! (West mógł tak, nieco żartobliwie, powiedzieć jako uczeń Andersona, obecnego w czasie wykładu na sali).
Podstawowym wczesnym pojęciem był Z-zbiór (patrz Chapman, Lectures on Hilbert Cube Manifoldes, ISBN 0-8218-1678-0). Wprowadzili je niezależnie i opublikowali w tym samym czasie Anderson i Włodzimierz Holsztyński (w różnych czasopismach; tylko wcześniej wymieniona publikacja była zauważona).
Wśród wczesnych specjalistów należy wymienić, między innymi, Czesława Bessagę i Victora Klee.
Teoria grafów (05Cxx)[edytuj | edytuj kod]

Na pograniczu topologii oraz matematyki dyskretnej znajduje się ważna dziedzina, zwana teorią grafów. Najprostszy graf można sobie wyobrazić jako zbiór punktów (tzw. wierzchołków), z których niektóre połączone są liniami (tzw. krawędziami). Historycznie pierwsze zadanie topologii, dotyczące mostów królewieckich, zalicza się do tej dziedziny. Słynnym problemem teorii grafów, który bardzo długo opierał się udowodnieniu, było twierdzenie o czterech barwach, głoszące, że dowolną mapę polityczną, na której każdy kraj składa się z jednego tylko kawałka (na sferze lub płaszczyźnie – to przypadki równoważne), można zabarwić używając tylko czterech kolorów tak, aby żadne dwa kraje mające wspólną granicę (dłuższą niż punkt) nie miały tego samego koloru (zobacz rysunek).
Klasycznym wynikiem teorii grafów jest twierdzenia Kazimierza Kuratowskiego, charakteryzujące topologicznie grafy płaskie.
Przykłady twierdzeń i wniosków z nich płynących[edytuj | edytuj kod]
- W Waszyngtonie, w miejscu upamiętniającym amerykańskich marynarzy z czasów II wojny światowej (United States Navy Memorial) znajduje się mapa świata ułożona z materiałów tworzących chodnik na dużym placu (zobacz zdjęcia poniżej). Z wyjątkiem zniekształceń na obwodzie tej mapy, jest ona ciągłą reprezentacją powierzchni Ziemi w pewnej skali. Jednak wyłącznie na podstawie twierdzenia Banacha o odwzorowaniu zwężającym nie możemy powiedzieć, że jest punkt na tej mapie, który odpowiada samemu sobie (tzn. ten punkt i jego reprezentacja na mapie pokrywają się). Bowiem cała (idealizowana) powierzchnia Ziemi nie jest odwzorowana na mapę w sposób ciągły. Możemy jednak ograniczyć się do powierzchni kontynentalnej części USA (bez Alaski). Ponieważ cała mapa (chodnik) znajduje się w USA, to twierdzenie Banacha możemy zastosować wyłącznie do powierzchni USA: istnieje punkt powierzchni USA, który na chodnikowej mapie jest reprezentowany przez samego siebie (tj. reprezentujący go punkt mapy pokrywa się z nim). Chodzi o to, że o ile cała powierzchnia Ziemi na mapie jest rozcięta, to powierzchnia kontynentalnego USA przedstawiona jest w sposób ciągły (i zwężający). Gdy pojawiają się cięcia, to sprawa się komplikuje. (Uwaga: Z Alaską na mapach różnie bywa – czasem jest pocięta, a czasem nie; skoro jednak cała mapa znajduje się na chodniku w części kontynentalnej USA, to o ewentualne pocięcie Alaski nie musimy się martwić).
-
US Navy Memorial w Waszyngtonie: mapa świata.
-
Fragment mapy świata przedstawiający Stany Zjednoczone.
-
W części mapy przedstawiającej Wschodnie Wybrzeże Stanów Zjednoczonych znajduje się dokładnie jeden punkt, który odpowiada samemu sobie w terenie.
- Na podstawie twierdzenia Borsuka-Ulama możemy stwierdzić, że w każdym momencie są na Ziemi dwa punkty antypodyczne, w których zarówno temperatura, jak i ciśnienie powietrza są takie same, przy założeniu, że temperatura i ciśnienie zmieniają się w sposób ciągły. Przypomnijmy, że twierdzenie Borsuka-Ulama mówi, że dla każdej ciągłej funkcji (gdzie jest sferą -wymiarową) istnieją dwa punkty antypodyczne dla których
- Twierdzenie Lusternika-Schirelmanna-Borsuka mówi, że jeśli sfera jest pokryta przez zbiorów, z których każdy jest albo otwarty, albo domknięty, to jeden z tych zbiorów zawiera punkty antypodalne. (Wersja otwarta wynika w sposób elementarny z wersji domkniętej, i odwrotnie).
- Znana jest anegdota, według której twierdzenie to uratowało pewien wyimaginowany świat przed wielkim nieszczęściem:
- Rosja, Prusy i Austria postanowiły zakończyć wszystkie waśnie i podzielić się strefami wpływów. Każde z mocarstw chciało otrzymać część planety w wieczyste władanie. Z powodów związanych z bronią umieszczoną na satelitach żadne z mocarstw nie chciało, aby inne mocarstwo miało pod swoją kontrolą jakiekolwiek dwa punkty antypodalne. Lata prób nie doprowadziły do rozwiązania problemu, a ogłoszenie twierdzenia spowodowało, że trzy mocarstwa zadowoliły się podziałem Polski.
- Jeżeli spłaszczymy piłkę, to jakkolwiek byśmy jej przy tym nie deformowali (bez rozrywania), zawsze zetkną się jej dwa punkty antypodyczne. Jest to poglądowe sformułowanie powyższego twierdzenia Borsuka-Ulama o antypodach.
- Każdą kanapkę z żółtym serem i szynką można przeciąć nożem (czyli podzielić płaszczyzną) tak, by każda z dwóch części miała tyle samo chleba, tyle samo sera, i tyle samo szynki.
Przykład argumentacji topologicznej w analizie[edytuj | edytuj kod]
Metody topologiczne stosuje się w wielu rozważaniach matematycznych, począwszy od analizy, przez geometrię, równania różniczkowe, aż na algebrze skończywszy, gdyż dostarcza ona matematykom wspólnego języka umożliwiającego dość ogólne spojrzenie geometryczne na problemy.
Przykładem rozumowania topologicznego może być dowód twierdzenia o istnieniu funkcji ciągłej rzeczywistej, określonej na prostej rzeczywistej która nie jest różniczkowalna w żadnym punkcie. Pierwszy konkretny przykład takiej funkcji podał niemiecki matematyk Karl Weierstraß. Poszukiwanie kolejnych tego typu przykładów nastręczało wiele trudności, zastanawiano się nad ogólną formą i liczbą takich funkcji. Polski matematyk Stefan Banach przedstawił w 1931 topologiczny dowód istnienia takich funkcji:
- Niech oznacza przestrzeń wszystkich funkcji ciągłych z odcinka w zbiór liczb rzeczywistych. Przestrzeń można wyposażyć w topologię zbieżności jednostajnej poprzez metrykę
- Wówczas jest przestrzenią polską (a nawet przestrzenią Banacha), w której zbiór
- ma pochodną w co najmniej jednym punkcie odcinka
- jest pierwszej kategorii. Ponieważ przestrzeń jest zupełna (a więc jest przestrzenią Baire’a), to można powiedzieć, że z topologicznego punktu widzenia prawie każda funkcja ciągła nie jest różniczkowalna w żadnym punkcie.
Dowód ten wykazuje istnienie funkcji nieróżniczkowalnych w żadnym punkcie, jednak nie wskazuje konkretnego przykładu takiej funkcji.
Polscy topolodzy[edytuj | edytuj kod]
Głównym ośrodkiem rozwoju topologii w Polsce była Warszawska szkoła matematyczna, współpracująca z lwowską szkołą matematyczną. Wśród polskich matematyków wkład w rozwój topologii wnieśli, między innymi:
- Kazimierz Alster
- Stefan Banach
- Czesław Bessaga
- Karol Borsuk
- Janusz Jerzy Charatonik
- Tadeusz Dobrowolski
- Roman Duda
- Samuel Eilenberg
- Ryszard Engelking
- Witold Hurewicz
- Zygmunt Janiszewski
- Jan Jaworowski
- Andrzej Kirkor
- Bronisław Knaster
- Antoni A. Kosiński
- Krystyna Kuperberg
- Włodzimierz Kuperberg
- Kazimierz Kuratowski
- Jerzy Mogilski
- Stanisław Mrówka
- Andrzej Lelek
- Edward Marczewski
- Stefan Mazurkiewicz
- Jerzy Mioduszewski
- Jan Mycielski
- Hanna Patkowska
- Aleksander Pełczyński
- Juliusz Paweł Schauder
- Karol Sieklucki
- Wacław Sierpiński
- Roman Sikorski
- Andrzej Szankowski
- Henryk Toruńczyk
- Menahem Wojdysławski
- Kazimierz Zarankiewicz
Zobacz też[edytuj | edytuj kod]
Uwagi[edytuj | edytuj kod]
- ↑ Formalnie „za wkład w geometrię oraz za rewolucyjne odkrycia dotyczące analitycznej i geometrycznej struktury potoku Ricciego”[8].
- ↑ David J. Thouless, Duncan Haldane i John M. Kosterlitz otrzymali ją „za teoretyczne odkrycia w dziedzinie topologicznych przejść fazowych i topologicznych faz materii”.
Przypisy[edytuj | edytuj kod]
- ↑ a b c d e f topologia, [w:] Encyklopedia PWN [dostęp 2022-02-04].
- ↑
 Joanna Jaszuńska, Zabawy z plasteliną, deltami.edu.pl, styczeń 2011 [dostęp 2022-02-05].
Joanna Jaszuńska, Zabawy z plasteliną, deltami.edu.pl, styczeń 2011 [dostęp 2022-02-05].
- ↑ Richard Courant, Herbert Robbins: Co to jest matematyka?, Wydanie uzupełnione przez Iana Stewarta, Prószyński i Spółka, Warszawa 1998, ISBN 83-7180-005-3.
- ↑
 Aleksander Błaszczyk, Zbiory liczbowe widziane oczami topologa, math.us.edu.pl, 25 września 2018 [dostęp 2022-02-05].
Aleksander Błaszczyk, Zbiory liczbowe widziane oczami topologa, math.us.edu.pl, 25 września 2018 [dostęp 2022-02-05].
- ↑
 Karol Gryszka, Liczb pierwszych jest nieskończenie wiele, deltami.edu.pl, październik 2021 [dostęp 2022-02-05].
Karol Gryszka, Liczb pierwszych jest nieskończenie wiele, deltami.edu.pl, październik 2021 [dostęp 2022-02-05].
- ↑ przestrzeń topologiczna, [w:] Encyklopedia PWN [dostęp 2022-02-04].
- ↑ topologia geometryczna, [w:] Encyklopedia PWN [dostęp 2022-02-04].
- ↑ Jenny Hogan. Maths ‘Nobel’ prize declined by Russian recluse. „Nature”, 2006-08-22. DOI: 10.1038/news060821-5. ISSN 1476-4687. (ang.).
- ↑
 Nowy ważny krok na drodze do topologicznego komputera kwantowego, naukawpolsce.pl, 18 sierpnia 2017 [dostęp 2022-02-05].
Nowy ważny krok na drodze do topologicznego komputera kwantowego, naukawpolsce.pl, 18 sierpnia 2017 [dostęp 2022-02-05].
- ↑
 Stanisław Bajtlik, Kształt wszechświata, kanał „Zapytaj fizyka” na YouTube, 20 marca 2015 [dostęp 2022-02-05].
Stanisław Bajtlik, Kształt wszechświata, kanał „Zapytaj fizyka” na YouTube, 20 marca 2015 [dostęp 2022-02-05].
- ↑ Jerzy Mioduszewski. Mosty królewieckie. Dwieście lat później. „Delta”. 4 (1981). [dostęp 2021-09-01].
- ↑ Mariusz Śliwiński: Mosty królewieckie. math.edu.pl. [dostęp 2014-09-11].
- ↑ a b Iwo Białynicki-Birula, Iwona Białynicka-Birula: Modelowanie rzeczywistości. Warszawa: Prószyński i S-ka SA, 2002, s. 14–18. ISBN 83-7255-103-0.
- ↑ Johann Benedict Listing, Vorstudien zur Topologie, Vandenhoeck und Ruprecht, Göttingen 1848, s. 67.
- ↑ Bernhard Riemann: Über die Hypothesen welche der Geometrie zu Grunde liegen. Treść wykładu w j. ang.: [1].
- ↑ Henri Poincaré: Analysis situs. „J. de l’Éc. Pol.” (2) I, (1895), s. 1–123.
- ↑ Maurice Fréchet: Sur quelques points du calcul fonctionnel. „Rend. del Circ. Mat. di Palermo” 22, (1906), s. 1–74.
- ↑ Kazimierz Kuratowski: Sur l’opération de l’Analysis Situs. „Fundamenta Mathematicae” 3, (1922), s. 182–199.
- ↑ topologia ogólna, [w:] Encyklopedia PWN [dostęp 2022-02-05].
- ↑ В.Г. Болтянский, Пример двумерного компакта, топологический квадрат которого имеет размерность равную трем, ДАН, 67 (1949), s. 597–599.
- ↑ a b Włodzimierz Holsztyński, Une generalisation du théorème de Brouver sur les points invariants, „Bull. Polon. Acad. Sci.” 12, (1964), s. 603–609.
Bibliografia[edytuj | edytuj kod]
Na polskim rynku wydawniczym istnieją podręczniki akademickie poświęcone topologii, m.in.:
- Kazimierz Kuratowski: Wstęp do teorii mnogości i topologii (wraz z dodatkiem Ryszarda Engelkinga Elementy topologii algebraicznej), wyd. siódme rozszerzone, Biblioteka Matematyczna. Tom 9, Państwowe Wydawnictwo Naukowe, Warszawa 1977.
- Ryszard Engelking: Topologia ogólna. Biblioteka Matematyczna. Tom 47. Państwowe Wydawnictwo Naukowe, Warszawa 1975.
- Hanna Patkowska: Wstęp do topologii, Państwowe Wydawnictwo Naukowe, Warszawa, 1979.
- Ryszard Engelking, Karol Sieklucki: Geometria i topologia. Część II. Topologia. Biblioteka Matematyczna. Tom 54, Państwowe Wydawnictwo Naukowe, Warszawa 1980. ISBN 83-01-01371-0.
- Roman Duda, Wprowadzenie do topologii. Cz. I. Topologia ogólna, Cz. II. Topologia algebraiczna. Topologia rozmaitości. Biblioteka Matematyczna. Tom 61, Państwowe Wydawnictwo Naukowe, Warszawa 1986. ISBN 83-01-05714-9.
Linki zewnętrzne[edytuj | edytuj kod]
- B. Franzosa, Wstęp do topologii (Youtube, ang.)
- Eric W. Weisstein, Topology, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2023-06-01].
 General topology (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-06-18].
General topology (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-06-18].

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle [0,1]\times [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f68b48bb3a24791592c1a0e8967bdef5d3409c)



























![{\displaystyle C[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e160d783783c799aae07cf78d250747461af0ff9)
![{\displaystyle d(f,g)=\sup _{x\in [0,1]}|f(x)-g(x)|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4968cb9f2028481e49bb5c4a09a337ae1840ce7)
![{\displaystyle R={\big \{}f\in C[0,1]\colon f}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f239682e49f9575712a29262ebd7c6bd8c1dc4c5)
![{\displaystyle [0,1]{\big \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2ce0ccfd716549a51ef92282acfacce9f2fefb0)
