Układ równań liniowych
| Ten artykuł od 2016-10 wymaga zweryfikowania podanych informacji. |
Układ równań liniowych – koniunkcja pewnej liczby (być może nieskończonej[1]) równań liniowych, czyli równań pierwszego rzędu.
Teoria układów równań liniowych jest działem algebry liniowej leżącej u podstaw nowoczesnej matematyki. Algorytmami obliczeniowymi zajmuje się dział nazywany numeryczna algebra liniowa, same zaś metody odgrywają ważną rolę w inżynierii, fizyce, chemii, informatyce i ekonomii. Częstokroć aproksymuje (przybliża) się bardziej skomplikowane układy równań nieliniowych (opisujące modele matematyczne czy symulacje komputerowe) dużo prostszymi układami równań liniowych (tzw. linearyzacja).
Układy równań liniowych rozpatruje się najczęściej nad ciałami (np. liczbami wymiernymi, rzeczywistymi czy zespolonymi); choć ma to sens już w przypadku pierścieni (np. liczb całkowitych), to rozwiązywanie takich układów nastręcza znacznie więcej trudności (w szczególności oznacza to badanie modułów zamiast przestrzeni liniowych, zob. uogólnienia). W dalszej części przyjmuje się, że wszystkie współczynniki należą do ustalonego ciała.
Motywacje[edytuj | edytuj kod]
W geometrii euklidesowej można rozpatrywać miejsca geometryczne wyznaczone przez dane dwie proste na płaszczyźnie – mogą one wyznaczać prostą, punkt lub nie wyznaczać żadnego miejsca geometrycznego; odpowiada im odpowiednio nieskończony zbiór elementów, zbiór złożony z pojedynczego elementu lub zbiór pusty. Wprowadzenie na płaszczyźnie układu współrzędnych umożliwia algebraizację tego zadania: proste zadane są za pomocą równań liniowych, zaś miejsce geometryczne wyznaczone przez te proste odpowiada zbiorowi elementów spełniających wszystkie równania jednocześnie (pełną interpretację geometryczną można znaleźć w sekcji Uogólnienia).

Jeśli w układzie współrzędnych kartezjańskich proste zadane są równaniami
oraz
to ich jedyny punkt wspólny ma współrzędne co łatwo sprawdzić wprost:
To, że jest to jedyny punkt, wynika z faktu, iż proste te nie są równoległe (argument formalny podano dalej). Zwyczajowo równania prostych zapisuje się bezpośrednio jedno pod drugim i spina klamrą:
nazywając je układem równań liniowych, zaś zbiór elementów spełniających każde równanie z osobna (odpowiadający punktom wspólnym prostych) – jego rozwiązaniami.
Postać i zapis[edytuj | edytuj kod]
Niech oznacza układ równań liniowych o niewiadomych, tzn. [2]
Niech oraz Wielkości nazywa się niewiadomymi (lub zmiennymi), liczby nazywa się współczynnikami, zaś elementy to wyrazy wolne. Układ nazywa się jednorodnym, jeżeli wyrazy wolne są równe zeru; inaczej mówiąc, wszystkie równania jednorodnego układu równań liniowych są jednorodne.
Układ można zapisać jako równanie wektorowe
które można przedstawić w postaci
dzięki czemu każda niewiadoma może być postrzegana jako współczynnik kombinacji liniowej wektorów tzn.
gdzie nazywa się w tym kontekście wektorem wyrazów wolnych, zaś to wektor zmiennych (zob. uogólnienia).
Korzystając z notacji macierzowej, układ można przedstawić w postaci
co, przy pomocy standardowego mnożenia macierzy, można zapisać w formie

Innymi słowy dowolny układ można traktować jak macierzowe równanie liniowe
gdzie jest macierzą typu zaś oraz to macierze odpowiednio typów oraz Macierz nazywa się macierzą główną układu Jeśli macierz układu jest kwadratowa, tzn. to sam układ również nazywa się czasem kwadratowym, jeśli jest ona prostokątna, czyli to układ także nazywa się niekiedy prostokątnym.
Ponieważ macierz w powyższym równaniu macierzowym zachowuje się przy operacjach elementarnych na wierszach (każde równanie jest kombinacją liniową elementów ), to wygodne jest pominięcie go w zapisie i rozpatrywanie macierzy rozszerzonej bądź uzupełnionej układu złożonej z elementów macierzy oraz w której wyrazy oddziela się zwykle optycznie od wyrazów pionową kreską:
Macierz może być traktowana jako przypadek szczególny macierzy rozszerzonej, w której wyrazy są równe zeru.
Dowolny układ można zapisać w postaci
co w zapisie macierzowym można ująć następująco:
W ten sposób układ w postaci można zapisać jako
gdzie jest macierzą typu zaś jest macierzą typu a jest macierzą zerową typu Macierz główna układu jest więc formalnie macierzą rozszerzoną układu Oznacza to, że układ niejednorodny zmiennych można sprowadzić do układu jednorodnego zmiennych, przy czym jedna z nich jest ustalona (zob. uogólnienia).
Rozwiązania[edytuj | edytuj kod]

Rozwiązaniem nazywa się dowolny ciąg liczb który po podstawieniu za będzie spełniał każde z równań Układ, który nie ma rozwiązań, nazywa się sprzecznym; jeżeli zbiór rozwiązań układu jest niepusty, to nazywa się go niesprzecznym. Układ niesprzeczny, który ma jedno i tylko jedno rozwiązanie, nazywa się oznaczonym; układy o więcej niż jednym rozwiązaniu nazywa się nieoznaczonymi – w przypadku układów liniowych nad ciałami nieskończonymi (takimi jak liczby wymierne, liczby rzeczywiste czy liczby zespolone) oznacza to, że układ ma nieskończenie wiele rozwiązań.
Wskazówkę co do ogólnej liczby rozwiązań układu daje już sama jego postać:
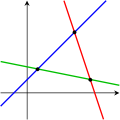
- układ niedookreślony, który ma mniej równań niż niewiadomych, zwykle jest nieoznaczony;
- układ nadokreślony mający więcej równań niż niewiadomych, zazwyczaj jest sprzeczny;
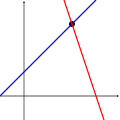
- układ, który ma tyle równań co niewiadomych, często ma jedno rozwiązanie.
Przypadki te obrazują następujące wykresy dla układów równań liniowych dwóch zmiennych:
Operacje elementarne[edytuj | edytuj kod]
Podstawową metodą rozwiązywania układów równań jest przekształcanie danego układu w inny, który ma ten sam zbiór rozwiązań – układy takie nazywa się równoważnymi. Można wyróżnić trzy operacje elementarne na wierszach przekształcające dany układ w układ do niego równoważny:
- dodanie do równania innego równania pomnożonego przez liczbę,
- zamiana dwóch równań miejscami,
- pomnożenie równania przez liczbę różną od zera.
Powszechnie stosowanymi metodami rozwiązywania układów równań liniowych za pomocą wspomnianych operacji elementarnych są:
- metoda eliminacji Gaussa, w której układ przekształca się do równoważnego z nim układu równań z rosnącą liczbą zmiennych;
- metoda eliminacji Gaussa-Jordana, w której układ przekształca się dalej (poprzez kolejne podstawienia równań z mniejszą liczbą zmiennych do tych z większą) do równoważnego z nim układu równań liniowych wiążących bezpośrednio każdą zmienną z pewną wartością.
Oba algorytmy opisano w przypadku, gdy układ jest oznaczony. Jeśli układ jest sprzeczny, to uzyskuje się (co najmniej jedno) równanie sprzeczne, które mówi o sprzeczności całego układu. Jeśli układ jest nieoznaczony, to niektóre zmienne przenosi się do prawych części równań i rozwiązanie podaje się w postaci wyrażania jednych zmiennych przez inne (zob. też następną podsekcję). Metody te w zapisie macierzowym odpowiadają (zwykle) najefektywniejszym metodom przekształcania macierzy głównej (w przypadku jednorodnym) lub rozszerzonej (w przypadku niejednorodnym) układu do wierszowo z nią równoważnej macierzy schodkowej w metodzie Gaussa i macierzy schodkowej zredukowanej w metodzie Gaussa-Jordana.
Opis ogólny i zależność[edytuj | edytuj kod]

Jeżeli układ ma więcej niż jedno rozwiązanie, to można je scharakteryzować, podając tzw. rozwiązanie ogólne układu, będące w istocie układem równań w prostej postaci – w przypadku, jeśli układ ma jedno rozwiązanie, to rozwiązanie można odczytać wprost z rozwiązania ogólnego. Układ
gdzie a zmienne nie występują po prawej stronie równań (tzn. dla ) zadaje rozwiązanie ogólne układu (krótko: jest rozwiązaniem ogólnym układu ). Zmienne nazywa się wtedy zależnymi, a pozostałe nazywa się wówczas zmiennymi niezależnymi (albo parametrami).
Równania w układzie liniowym nazywa się niezależnymi, jeśli żadne z nich nie może być uzyskane z innych za pomocą operacji elementarnych. Innymi słowy każde z nich zawiera nową informację o zmiennych i usunięcie któregokolwiek z nich powiększa liczbę rozwiązań; w przypadku równań liniowych niezależność ta nazywana jest niezależnością liniową (zob. charakteryzacja).
Wzory Cramera[edytuj | edytuj kod]
Jeśli macierz główna układu jest kwadratowa (układ jest kwadratowy), to oznaczoność układu jest równoważna odwracalności jego macierzy głównej. Macierz jest odwracalna wtedy i tylko wtedy, gdy jest nieosobliwa, tzn. ma niezerowy wyznacznik. Wówczas, mnożąc z lewej strony (w ogólności mnożenie macierzy nie jest przemienne) równanie
przez macierz czyli otrzymuje się rozwiązanie
Macierz odwrotną do można wyznaczyć w dowolny sposób, np. korzystając z operacji elementarnych bądź obliczając iloraz macierzy dołączonej przez wyznacznik macierzy Pierwsza metoda odpowiada w istocie metodzie eliminacji Gaussa-Jordana, druga z kolei jest wnioskiem z twierdzenia Cramera:
wtedy też, na mocy rozwinięcia Laplace’a, wzory na elementy powyższej macierzy, nazywane właśnie wzorami Cramera, dane są jako ilorazy wyznaczników macierzy przez wyznacznik macierzy głównej układu
gdzie oznacza macierz powstałą z poprzez zamianę elementów -tej kolumny elementami macierzy wyrazów wolnych o ile tylko nie jest równy zeru.
Jak już wspomniano, układ jest oznaczony, gdy macierz główna jest odwracalna. Jeżeli wyznacznik macierzy głównej jest zerowy, to układ jest sprzeczny, gdy którykolwiek z wyznaczników jest niezerowy. Twierdzenie odwrotne nie jest prawdziwe: jeśli wszystkie wyznaczniki są zerowe, to układ nie musi być nieoznaczony (wiadomo jedynie, że nie jest oznaczony, czyli może być tak sprzeczny, jak i nieoznaczony).
Stosowanie wzorów Cramera do rozwiązywania „konkretnych” układów wymaga z reguły więcej obliczeń niż stosowanie metody Gaussa, jednak metoda Cramera bywa dogodniejsza w rozważaniach teoretycznych.
Inne metody[edytuj | edytuj kod]
Układy trzech czy nawet czterech zmiennych łatwo rozwiązać ręcznie (najlepiej metodą Gaussa); do większych stosuje się często komputery. Standardowe podejście opiera się na metodzie eliminacji Gaussa. Bardzo ważne jest unikanie dzielenia przez małe liczby, które może prowadzić do błędów zaokrągleń – można to osiągnąć poprzez zmianę kolejności równań (druga operacja elementarna). Ponadto w szczególnym przypadku, gdy dane układy mają tę samą macierz główną, lecz różne macierze rozszerzone (tzn. układy mają te same współczynniki, lecz różne wyrazy wolne), to pomocne okazuje się wyznaczenie rozkładu LU macierzy głównej.
Często możliwe jest wykorzystanie szczególnej postaci macierzy głównej układu do uzyskania szybszych bądź dokładniejszych algorytmów. Przykładowo układy z symetrycznymi i dodatnio określonymi macierzami głównymi mogą być rozwiązane dużo szybciej za pomocą rozkładu Cholesky’ego. Rekursja Levinsona jest z kolei szybką metodą rozwiązywania układów opisanych macierzą Toeplitza. Istnieją także specjalne metody dla macierzy z wieloma zerami (tzw. macierzy rzadkich), które pojawiają się często w zastosowaniach matematyki.
W zupełnie inny sposób podchodzi się do bardzo dużych układów, których rozwiązanie kosztowałoby zbyt dużo czasu lub pamięci. Idea polega na rozpoczęciu od wstępnego przybliżenia rozwiązania (które wcale nie musi być dokładne) i stopniowym jego poprawianiu. Jeśli jest ono wystarczająco dokładne, to właśnie ono przyjmowane jest jako rozwiązanie układu. Tego rodzaju podejście prowadzi do metod iteracyjnych.
Charakteryzacja[edytuj | edytuj kod]

O niesprzeczności i liczbie rozwiązań układu równań liniowych o niewiadomych mówi twierdzenie Kroneckera-Capellego: ma on rozwiązanie wtedy i tylko wtedy, gdy rząd macierzy głównej tego układu jest równy rzędowi jego macierzy rozszerzonej. Układ jednorodny zawsze ma rozwiązanie trywialne, tzn. postaci jest to jedyne rozwiązanie oznaczonego układu jednorodnego. Układ niesprzeczny jest
- oznaczony, tzn. ma jedno rozwiązanie, gdy rząd macierz głównej układu jest równy liczbie niewiadomych;
- nieoznaczony, tzn. nieskończenie wiele rozwiązań, gdy rząd macierzy głównej układu jest mniejszy od liczby niewiadomych – zbiór rozwiązań zależy wtedy od parametrów.
Z punktu widzenia geometrii analitycznej rozwiązania układu tworzą przestrzeń liniową (w przypadku jednorodnym) albo przestrzeń afiniczną (w przypadku niejednorodnym) wymiaru W szczególności więc, jeśli to rozwiązaniem jest punkt.
Niech oznacza zbiór rozwiązań układu jednorodnego Ponieważ układ jest jednorodny, to nie jest pusty. Niech należą do tzn. oraz skąd czyli również należy do a więc jest podprzestrzenią liniową przestrzeni współrzędnych. Ponieważ przekształcenie macierzy układu do postaci schodkowej zredukowanej nie zmienia zbioru rozwiązań układu, to pierwsze wierszy jest kombinacją liniową ostatnich liniowo niezależnych wierszy; w ten sposób również kolumn tej macierzy tworzy bazę przestrzeni (w gruncie rzeczy wykorzystuje się tu pojęcie rzędu; w ogólności powyższe obserwacje są równoważne twierdzeniu o rzędzie przekształcenia liniowego).
Teraz niech będzie zbiorem rozwiązań układu niejednorodnego ponieważ to zbiór ten nie jest pusty. Niech będzie ustalonym rozwiązaniem, a dowolnym rozwiązaniem układu; wówczas z oraz wynika czyli należy do zbioru rozwiązań odpowiadającego mu układu jednorodnego. Wraz z nim do należy również rozwiązanie przeciwne skąd co wobec dowolności oznacza Jeśli zaś gdzie należy do a należy do to czyli należy do a więc Wynika stąd, że zbiór rozwiązań układu niejednorodnego jest warstwą podprzestrzeni liniowej rozwiązań odpowiadającego mu układu jednorodnego, zatem jest podprzestrzenią afiniczną tej samej przestrzeni współrzędnych.
Uogólnienia[edytuj | edytuj kod]
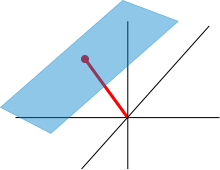
Z punktu widzenia geometrii analitycznej układ równań o zmiennych odpowiada zadaniu hiperpłaszczyzn w -wymiarowej przestrzeni liniowej (lub przestrzeni afinicznej), rozwiązaniem (ogólnym) jest wtedy przestrzeń będąca częścią wspólną wszystkich hiperpłaszczyzn.
Stosując notację wektorową, można wykorzystać do opisu układów równań liniowych cały aparat algebry liniowej. Zbiór wszystkich kombinacji liniowych układu wektorów nazywa się powłoką liniową; w ten sposób układ równań ma rozwiązanie, jeśli wektor leży w powłoce generowanej przez wektory Jeżeli każdy wektor powłoki można wyrazić jednoznacznie jako kombinację liniową wektorów to układ jest oznaczony. W każdej powłoce można wyróżnić bazę złożoną z liniowo niezależnych wektorów, dzięki którym wspomniane wyrażenie może być jednoznaczne; liczba wektorów w bazie (wymiar) nie może być większy niż czy ale może być mniejsza. Rozwiązanie istnieje, gdy powłoka składa się z liniowo niezależnych wektorów.
Najogólniejszą postacią przekształcenia liniowego między dwoma przestrzeniami liniowymi jest kombinacja liniowa zadających go wektorów (zob. twierdzenie o przekształceniu liniowym zadanym na bazie). Samo przekształcenie liniowe przy ustalonych bazach dziedziny i przeciwdziedziny, można zapisać w postaci macierzy Wówczas obliczaniu wartości odpowiada mnożenie a rozwiązywanie układu równań jednorodnych jest w istocie wyznaczaniem miejsc zerowych przekształcenia liniowego Przedstawione w poprzedniej sekcji rozumowanie jest przypadkiem szczególnym ogólnego wyniku – zbiór miejsc zerowych przekształcenia liniowego, nazywany jego jądrem, tworzy podprzestrzeń liniową w dziedzinie tego przekształcenia. Wymiar powłoki wspomniany w poprzednim akapicie w przypadku macierzy nazywa się jej rzędem (wierszowym). W ten sposób układ równań liniowych można traktować jako problem opisu przekształcenia liniowego przy czym istnienie rozwiązań jest tożsame z należeniem do obrazu (czyli istnieniem takiego wektora który spełniałby ), a ich jednoznaczność jest równoważna trywialności jądra (czyli różnowartościowości przekształcenia). Zależność między wymiarami jądra i obrazu opisuje tzw. twierdzenie o rzędzie przekształcenia liniowego.
Powyższe obserwacje dotyczące przestrzeni i przekształceń liniowych dla układów jednorodnych zachodzą mutatis mutandis dla przestrzeni i przekształceń afinicznych w przypadku niejednorodnym. W szczególności dowolne rozwiązanie układu niejednorodnego jest translacją rozwiązania odpowiadającego mu układu jednorodnego. Ponadto przekształceniu afinicznemu przestrzeni -wymiarowej w przestrzeń -wymiarową odpowiada przekształcenie liniowe
przestrzeni -wymiarowej w przestrzeń -wymiarową (każda przestrzeń afiniczna może być zanurzona w przestrzeni liniowej wyższego wymiaru). Ostatni wiersz macierzy można pominąć bez utraty ogólności, co tłumaczy obserwację poczynioną w sekcji postać i zapis.
Przypisy[edytuj | edytuj kod]
- ↑ F.P. Sayer. Some Aspects of Infinite Systems of Linear Simultaneous Equations. „IMA Journal of Numerical Analysis”. 1983 3(3):333-340. DOI: 10.1093/imanum/3.3.333. [dostęp 2009-01-06].
- ↑ Układ równań liniowych, [w:] Encyklopedia PWN [dostęp 2021-07-22].
Linki zewnętrzne[edytuj | edytuj kod]
- Opisowe rozwiązywanie układów równań liniowych online. sole.ooz.ie. [zarchiwizowane z tego adresu (2011-07-21)].
- Eric W. Weisstein, Linear System of Equations, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2024-03-07].























![{\displaystyle [x_{1}a_{11}+\ldots +x_{n}a_{1n},\ \dots ,\ x_{1}a_{m1}+\ldots +x_{n}a_{mn}]=[b_{1},\dots ,b_{m}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9f185cc4e991999a82af467fe41b5640d163951)
![{\displaystyle x_{1}[a_{11},\dots ,a_{m1}]+\ldots +x_{n}[a_{1n},\dots ,a_{mn}]=[b_{1},\dots ,b_{m}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ad139cb7731982419f2efba79e20cd3a3502bf)
![{\displaystyle \mathbf {a} _{j}=[a_{1j},\dots ,a_{mj}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275d32ee10d2396de3fb687924f10d71bfadac4e)

![{\displaystyle \mathbf {b} =[b_{1},b_{2},\dots ,b_{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/540b57b7a00dcd1b3dae680c887fc96910e34603)
![{\displaystyle \mathbf {x} =[x_{1},x_{2},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d269b0e9302ba60f60bc46bba5b14a8894365893)



![{\displaystyle \mathbf {A} =[a_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6af7018a97ea90ad130969ed51d0de89a030ff00)

![{\displaystyle \mathbf {X} =[x_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91d4e9c592e893f1e004903332da4660b603a528)
![{\displaystyle \mathbf {B} =[b_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a60dc20f4f54c6dab0a66a66b1d555a294f10aac)









![{\displaystyle \left[{\begin{matrix}a_{11}&a_{12}&\dots &a_{1n}\\a_{21}&a_{22}&\dots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\dots &a_{mn}\end{matrix}}\right|\left.{\begin{matrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{matrix}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb69654625603c5d8e5da268244c5653a7652c30)













































































![{\displaystyle \mathbf {A} =[\mathbf {a} _{j}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d350bc008e4ca4b19c9b5552762b512a4113a861)









