Małe twierdzenie Fermata

Małe twierdzenie Fermata (MTF) – twierdzenie teorii liczb sformułowane (bez dowodu) przez francuskiego matematyka Pierre'a de Fermata. Twierdzenie to jest podstawą dla testu pierwszości Fermata. Poniżej każdego sformułowania twierdzenia znajduje się zapis w arytmetyce modularnej.

Małe twierdzenie Fermata:

jeżeli $p$ jest liczbą pierwszą, to dla dowolnej liczby całkowitej $a$, liczba $a^p - a$ jest podzielna przez $p$.

$a^p - a \equiv 0 \pmod p$,

lub inaczej

jeśli $p$ jest liczbą pierwszą, a $a$ jest taką liczbą całkowitą, że liczby $a$ i $p$ są względnie pierwsze, to $a^{p-1} - 1$ dzieli się przez $p$. Innymi słowy,

$a^{p-1} - 1 \equiv 0 \pmod p$,

albo

$a^{p-1} \equiv 1 \pmod p$.

Dowody

Dowód z twierdzeniem Eulera

Jeżeli $p$ jest taką liczbą pierwszą, która nie dzieli $a$, to $p$ jest względnie pierwsze z $a$, a więc w myśl twierdzenia Eulera o liczbach względnie pierwszych teza twierdzenia jest prawdziwa.

Dowód kombinatoryczny

Bez straty ogólności można założyć, że $a$ jest liczbą naturalną. Rozpatrzmy wszystkie możliwe kolorowania koła podzielonego na p części za pomocą a kolorów. Kolorowania, które możemy na siebie nałożyć po obróceniu liczymy jako dwa różne. Wszystkich kolorowań jest $a^p$.

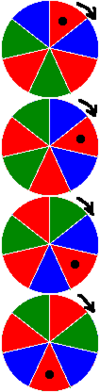
Wszystkie kolorowania, w których wykorzystaliśmy co najmniej dwa kolory możemy obracać tak, że otrzymamy zestawy po p parami różnych kolorowań, które są swoimi obrotami (przykładowe cztery z pewnego zestawu dla p=7, a=3 są przedstawione na rysunku). Jeżeli w pewnym zestawie utworzonym w ten sposób wystąpiłyby takie same kolorowania, to oznaczałoby to, że kąt pełny jest wielokrotnością pewnego kąta $\tfrac{2 \pi n}{p}$, o który trzeba obrócić jedno z tych kolorowań, aby otrzymać drugie. W przypadku, gdy wykorzystaliśmy więcej niż jeden kolor, nie jest to możliwe. Zatem

Liczba wszystkich kolorowań jest iloczynem $p$ i liczby zestawów po p kolorowań + liczba kolorowań jednokolorowych

$a^p = pn + a$,

gdzie n jest pewną liczbą naturalną.

Kolorów jest a, więc kolorowań jednokolorowych też jest a. Wynika stąd, że $p$ dzieli liczbę $a^p-a$.

Dowód wykorzystujący metody teorii grup

Zbiór $\mathbb Z_p^*=\{1, \ldots, p-1\}$ jest grupą z działaniem mnożenia modulo p, nazywaną multyplikatywną grupą klas reszt modulo p. Grupa ta jest rzędu $p-1$ (ma $p-1$ elementów). Niech $a$ będzie dowolnym elementem tej grupy. Oznaczmy przez $k$ rząd tego elementu, tzn. najmniejszą liczbę $k \in \mathbb N$ spełniającą warunek $a^k = 1$. Innymi słowy

$a^k \equiv 1 \pmod p$

Z twierdzenia Lagrange'a wynika, że rząd elementu $a$ dzieli rząd grupy $\mathbb Z_p^*$, czyli $k | p-1$. A zatem istnieje pewna liczba naturalna $m$ spełniająca warunek

$p-1 = km$

Wówczas

$a^{p-1} \equiv a^{km} \equiv (a^k)^m \equiv 1^m \equiv 1 \pmod p$.

Dowód indukcyjny

Załóżmy, że $a$ jest liczbą naturalną. Twierdzenie to jest prawdziwe, gdy $a = 1$. Zatem załóżmy indukcyjnie, że:

$a^p \equiv a \pmod p$ dla $a \geqslant 1$

wówczas:

$(a+1)^p = \sum_{k=0}^p{p \choose k}a^k = a^p + a^0 + \sum_{k=1}^{p-1}{p \choose k}a^k$

Ponieważ

${p \choose k} = \frac{p(p-1)(p-2)\cdots (p-k+1)}{k!}$

więc dla $0<k<p$ żaden z czynników k! nie jest równy $p$, dlatego ${p \choose k}$ jest wielokrotnością p. Zatem:

${p \choose k} \equiv 0 \pmod p$

Ostatecznie:

$(a+1)^p \equiv a^p + a^0 + \sum_{k=1}^{p-1}{p \choose k}a^k \equiv a^p + a^0 \equiv a + 1$

Zatem na mocy indukcji $a^p \equiv a \pmod p$, czyli p dzieli $a^p - a$.

Bibliografia

• Wacław Sierpiński: Arytmetyka teoretyczna. Wyd. 2. Warszawa: PWN, 1959, s. 144-147. 

Zobacz też

• liczby pseudopierwsze
• wielkie twierdzenie Fermata