Równanie Lotki-Volterry

Obraz przestrzeni fazowej (portret fazowy czyli trajektoria fazowa rozwiązań) dla układu Lotki-Volterry

Przebieg zmian liczby ofiar (prey) i drapieżników (predator) w czasie (wykres czasowy)

przebieg czasowy

Równanie Lotki-Volterry znane też jako model Lotki-Volterry lub model drapieżnik-ofiara to nieliniowe równanie różniczkowe pierwszego stopnia.

Poniższy model został zaproponowany w 1926 przez Vito Volterrę do opisu populacji ryb odławianych w Morzu Adriatyckim. Niezależnie od Volterry równoważne równania do opisu oscylacji stężeń substancji w hipotetycznej reakcji chemicznej otrzymał Alfred James Lotka w 1920 roku.

Równanie Lotki-Voltery stanowi model układów dynamicznych występujących w ekosystemach (np. w symulacji zachowania populacji ofiar i drapieżników).

Podstawowy model

Równanie zaproponowane przez autorów ma postać:

$\frac{dx}{dt} = (a - by)x$

$\frac{dy}{dt} = (cx - d)y$

gdzie: x(t) - populacja czyli liczba ofiar (ang. prey, np. zające), y(t) - liczba drapieżców (ang. predators, np. rysie), t - reprezentuje rozwój tych dwóch populacji w czasie natomiast stałe (a,b,c,d > 0, dodatnie parametry) oznaczają:

a - częstość narodzin ofiar lub współczynnik przyrostu ofiar,

b - częstość umierania ofiar na skutek drapieżnictwa,

c - częstość narodzin drapieżników lub współczynnik przyrostu drapieżników,

d - częstość umierania drapieżników lub współczynnik ubywania drapieżników,

Bardzo często do dalszej analizy własności tych równań przeprowadza się ich ubezwymiarowienie za pomocą następujących podstawień:
$u(\tau)=\frac{cx(t)}{d}$, $v(\tau)=\frac{by(t)}{a}$, $\tau=at$, $\alpha=\frac{d}{a}$
Powyższe podstawienie prowadzi do następującego układu równań, który zależy już tylko od jednego parametru $\alpha$:

$\frac{du}{d\tau}=u(1-v)$

$\frac{dv}{d\tau}=\alpha v(u-1)$

Punkty krytyczne tego układu to $(0,0)$ oraz $(1,1)$. Dalsza liniowa analiza prowadzi do wniosku, że punkt $(0,0)$ jest punktem siodłowym, zaś $(1,1)$ to centrum stabilne w sensie Lapunowa.

Uogólniony model Lotki-Volterry

Model Lotki-Volterry można uogólnić na większą ilość ($N$) oddziałujących ze sobą populacji. Wtedy otrzymamy następujący układ równań:

$\frac{dx_i}{dt} = (a_i - \sum_{j=1}^{N}{b_ij y_j})x_i$

$\frac{dy_i}{dt} = (\sum_{j=1}^{N} c_ij x_j - d_i)y_i$

gdzie parametry $a_i, b_{ij}, c_{ij}, d_i$ mają analogiczne znaczenie jak w modelu dwuwymiarowym.

Realistyczny model drapieżnik-ofiara

Wykres przedstawia zmiany populacji ofiar i drapieżników w czasie oraz wykres fazowy.

Wykres przedstawia płaszczyznę która oddziela przestrzeń fazową parametrów a,b i d. Dla punktów znajdujących się pod płaszczyzną wykresy fazowe dążą do cyklu stabilnego. Dla punktów powyżej płaszczyzny wykresy fazowe zdążają do ogniska.

Przykładowy przekrój dla parametru a = 1,4483, gdzie pokazana jest linia oddzielająca domenę z rozwiązaniami stabilnymi od tej niestabilnymi, zwaną krzywą bifurkacyjną. Nad linią punkt przedstawia przykładową kombinację parametrów b i d dla której mamy trajektorię fazową z punktem stabilnym. Pod linią punkt przedstawia przykładową kombinację parametrów b i d dla której mamy trajektorię fazową z punktem niestabilnym.

Główną wadą podstawowego modelu Lotki-Volterry jest fakt, że przy zerowej populacji drapieżników liczebność ofiar wzrasta nieograniczenie. Dlatego też w bardziej realistycznych modelach opisujących to zjawisko wprowadza się chociażby pojemność środowiska $K$ - czyli liczbę osobników jaką może maksymalnie osiągnąć dana populacja. Przykładowe równania uwzględniające ten czynnik wyglądają następująco:

$\frac{dx}{dt} = x\left(r\left(1-\frac{x}{K}\right)-\frac{ky}{x+D}\right)$

$\frac{dy}{dt} = y\left(s\left(1-\frac{hy}{x}\right)\right)$

$D, h, s$ to nieujemne stałe zależne od modelu.

Często warto zapisać równania w formie bezwymiarowej, by zmniejszyć liczbę parametrów. Powyższe równania skalujemy korzystając z następujących podstawień: $u(\tau)=\frac{x(t)}{K}$ , będzie ułamkiem pojemności środowiska jaki zajmują ofiary, zaś

$v(\tau)=\frac{hy(t)}{K}$ , określa ułamek pojemności

jaki zajmują drapieżnicy a $\tau = rt$ jest przeskalowanym czasem.

Parametry egzogeniczne skalujemy w następujący sposób:

$a= \frac{k}{hr}$ , $b=\frac{s}{r}$ , $d= \frac{D}{K}$

Otrzymujemy wtedy przeskalowane równania Lotki-Volterry w postaci: $\frac{du}{d\tau}=u(1-u)-\frac{auv}{u+d}$

$\frac{dv}{d\tau}=bv(1-\frac{v}{u})$

Po przyrównaniu prawych stron powyższych równań do zera i ich rozwiązaniu uzyskujemy jeden punkt osobliwy w I ćwiartce. Punkt ten jest stabilny jeśli parametry $a,b,d\;$ spełniają:

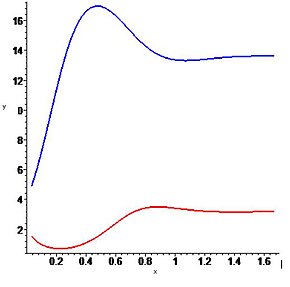
$b < [a-\{(1-a-d)\}^{\frac{1}{2}} \frac{[1+a+d-\{(1-a-d)^2 +4d\}^{\frac{1}{2}}]}{2a}$ Jeśli nierówność ta nie zachodzi to punkt jest niestabilny i z twierdzenia Poincare'go-Bendixson'a można wnioskować, że istnieje stabilny cykl graniczny w pierwszej ćwiartce płaszczyzny fazowej. Przestrzeń parametrów $(a,b,d)\;$ jest więc podzielona powierzchnią, pod którą układ dynamiczny realizuje cykl graniczny (więc populacje oscylują w czasie). Nad tą powierzchnią układ posiada jedno nietrywialne rozwiązanie stacjonarne (populację dążą asymptotycznie do stałych wartości).

Modyfikacje modelu Lotki-Volterry

Przebieg zmian liczby ofiar (prey) i drapieżników (predator) w czasie przy wewnętrznej konkurencji o żywność

W wyjściowym modelu wpływ na tempo wzrostu populacji mają tylko współczynniki umieralności i narodzin ofiar i drapieżników, podczas gdy w rzeczywistości na proces ten wpływa o wiele więcej czynników, np. konkurencja. Model można zmodyfikować o wpływ konkurencji o pożywienie na tempo wzrostu obu populacji. W efekcie otrzymujemy:

$\frac{dx}{dt} = (a - by)x - ex$

$\frac{dy}{dt} = (cx - d)y - fy$

gdzie e i f są współczynnikami konkurencji między osobnikami. Gdy jest dużo drapieżników, konkurują (walczą) między sobą o pożywienie. Natomiast, gdy jest dużo ofiar, maleje ilość pożywienia dla nich.

Innym, równie ważnym, czynnikiem wpływającym na tempo wzrostu obu populacji jest przepełnienie środowiska. Wprowadzając odpowiednie współczynniki, otrzymujemy nowy układ:

$\frac{dx}{dt} = (a - by)x - gx^2$

$\frac{dy}{dt} = (cx - d)y - hy^2$

gdzie g i h są współczynnikami umieralności związanej z przepełnieniem obszaru, na którym żyją oba gatunki.

Literatura

V. Volterra. Variations and fluctuations of the number of indviduals in animal species living together. In Animal Ecology. McGraw-Hill, 1931. Translated from 1928 edition by R. N. Chapman.

Linki zewnętrzne

• Równanie Lotki-Volterry (ang.) w encyklopedii MathWorld