Pochodna cząstkowa

Pochodna cząstkowa – dla danej funkcji wielu zmiennych pochodna względem jednej z jej zmiennych przy ustaleniu pozostałych (w przeciwieństwie do pochodnej zupełnej, w której zmieniać się mogą wszystkie zmienne). Pochodne cząstkowe znajdują zastosowanie np. w rachunku wektorowym oraz geometrii różniczkowej.

Pochodne cząstkowe funkcji $f$ względem zmiennej $x$ oznacza się symbolami

${\frac {\partial f}{\partial x}},\;f'_{x},\;f_{x}{\text{ lub }}\partial _{x}f.$

Symbol pochodnej cząstkowej ∂ ma wygląd zaokrąglonej litery „d”.

Historia

Pochodne cząstkowe nie wywodzą się, jak można przypuszczać, z funkcji wielu zmiennych, ale były efektem badań rodziny krzywych zależnych od badanego parametru. Leibniz w 1692 roku, rozwiązał problem obwiedni dla rodziny krzywych $V(x,y,a)=0,$ pokazując, że można usunąć $a$ z równania uzyskując ${\frac {\partial }{\partial a}}V(x,y,a)=0$ (używając współczesnej notacji).

Współczesna notacja, użyta została po raz pierwszy przez Adriena-Marie Legendre’a, stała się powszechna po jej ponownym wprowadzeniu przez Carla Gustava Jakoba Jacobiego; z tej przyczyny bywa określana jako „delta Jacobiego”.

Wprowadzenie

Wykres funkcji $z=f(x,y)=x^{2}+xy+y^{2}$

Wartość z w zależności od x, dla y=1 $(z=f(x)=x^{2}+x+1)$

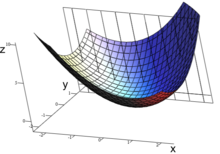
Niech $f$ będzie funkcją więcej niż jednej zmiennej. Przykładowo

$z=f(x,y)=x^{2}+xy+y^{2}.$

Wykres tej funkcji określa powierzchnię w przestrzeni euklidesowej. Istnieje nieskończenie wiele stycznych do każdego punktu tej powierzchni. Różniczkowanie cząstkowe polega na wybraniu jednej z tych prostych i uzyskaniu jej nachylenia. Zwykle najbardziej interesujące są proste, które są równoległe do płaszczyzny $xz$ czy $yz.$

Aby znaleźć nachylenie prostej stycznej do funkcji w $(1,1,3),$ która jest równoległa do płaszczyzny $xz$ należy traktować zmienną $y$ jak stałą. Wykres i wspomnianą płaszczyznę przedstawiono na rys. 1. Z kolei rys. 2. przedstawia wykres funkcji na płaszczyźnie $y=1.$ Szukając pochodnej wspomnianego równania przy założeniu, że $y$ jest stała, uzyskuje się nachylenie funkcji $f$ w punkcie $(x,y,z),$ którym jest

${\frac {\partial z}{\partial x}}=2x+y.$

W ten sposób okazuje się, poprzez podstawienie, że nachylenie w punkcie $(1,1,3)$ wynosi $3.$ Dlatego

${\frac {\partial z}{\partial x}}=3$

w punkcie $(1,1,3).$ Innymi słowy pochodna cząstkowa $z$ względem $x$ w punkcie $(1,1,3)$ jest równa $3.$

Definicja

Niech $U$ będzie otwartym podzbiorem przestrzeni euklidesowej $\mathbb {R} ^{n}$ i dane będą punkt $\mathrm {a} =(a_{1},\dots ,a_{n})$ oraz funkcja $f\colon U\to \mathbb {R} .$

Jeżeli istnieje skończona granica

$\lim _{h\to 0}{\frac {f(a_{1},\dots ,a_{k}+h,\dots ,a_{n})-f(a_{1},\dots ,a_{k},\dots ,a_{n})}{h}},$

to nazywa się ją pochodną cząstkową funkcji $f$ w punkcie $\mathrm {a}$ względem zmiennej $a_{k}$ i oznacza jednym z wyżej wymienionych symboli.

Związek z pochodną zupełną

Jeżeli oznaczyć $g(a_{k})=f(a_{1},\dots ,a_{k},\dots ,a_{n}),$ to

$f'_{x}(a_{1},\dots ,a_{k},\dots ,a_{n})=\lim _{h\to 0}{\frac {g(a_{k}+h)-g(a_{k})}{h}}$

jest po prostu pochodną $g'(a_{k})$ funkcji $g.$

Na przykład dla funkcji

$f(x,y)=x^{3}+3xy-y^{2}$

można obliczyć pochodne cząstkowe względem zmiennych $x$ i $y{:}$

${\frac {\partial f}{\partial x}}(x,y)=f'_{x}(x,y)=3x^{2}+3y,$

${\frac {\partial f}{\partial y}}(x,y)=f'_{y}(x,y)=3x-2y.$

Pochodne wyższych rzędów

Pochodne wyższych rzędów oblicza się, różniczkując znów po dowolnych zmiennych. Pochodne wyższych rzędów obliczane względem zmiennych różnych niż wybrana początkowo są znane jako pochodne mieszane.

Pochodne czyste

${\frac {\partial ^{2}f}{\partial x^{2}}}(x,y)=f''_{xx}(x,y)={\frac {\partial }{\partial x}}(3x^{2}+3y)=6x,$

${\frac {\partial ^{2}f}{\partial y^{2}}}(x,y)=f''_{yy}(x,y)={\frac {\partial }{\partial y}}(3x-2y)=-2$

i pochodne mieszane (różniczkowania zależnie od umowy należy wykonywać, tak jak w tym artykule, od lewej strony do prawej; bądź też, podobnie jak przy składaniu funkcji, od prawej do lewej)

${\frac {\partial ^{2}f}{\partial x\partial y}}(x,y)=f''_{yx}(x,y)={\frac {\partial }{\partial x}}(3x-2y)=3,$

${\frac {\partial ^{2}f}{\partial y\partial x}}(x,y)=f''_{xy}(x,y)={\frac {\partial }{\partial y}}(3x^{2}+3y)=3.$

Uogólnione twierdzenie Schwarza mówi, że jeśli wszystkie pochodne mieszane względem pewnych zmiennych są ciągłe w danym punkcie, ich wartość zależy wyłącznie od tego, względem których zmiennych różniczkujemy i ilekrotnie, natomiast nie zależy od kolejności w jakiej przeprowadza się różniczkowania.

Liczbę zastosowanych różniczkowań nazywamy rzędem pochodnej cząstkowej. Na przykład

${\frac {\partial ^{2}f}{\partial x{}\partial y}}{(x,y)}$

jest pochodną rzędu $2.$

Pochodne cząstkowe wyższych rzędów zapisuje się także z użyciem notacji wielowskaźnikowej. Wtedy przez $D^{\alpha }f,$ gdzie $\alpha =(\alpha _{1},\dots ,\alpha _{n})$ jest wielowskaźnikiem rozumie się

$D^{\alpha }f(x_{1},\dots ,x_{n})={\frac {\partial ^{\alpha _{1}}}{\partial x_{1}}}\ldots {\frac {\partial ^{\alpha _{n}}}{\partial x_{n}}}f(x_{1},\dots ,x_{n}).$

Rząd tej pochodnej cząstkowej wynosi oczywiście $|\alpha |=\alpha _{1}+\ldots +\alpha _{n}.$

Zobacz też

• dywergencja, rotacja
• gradient
• macierz Jacobiego
• operator Laplace’a
• operator d’Alemberta
• pochodna kierunkowa
• pochodna zewnętrzna
• pochodna zupełna

Bibliografia

• Witold Pogorzelski: Analiza matematyczna. T. II. Warszawa: Państwowe Wydawnictwo Naukowe, 1953, s. 10.
• Hans Niels Jahnke: A history of analysis. Providence, RI: American Mathematical Society, 2003. ISBN 0-8218-2623-9. OCLC 51607350.