Gradient (matematyka)

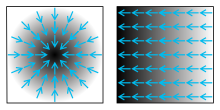
Gradient – w analizie matematycznej, a dokładniej rachunku wektorowym, pole wektorowe wskazujące kierunki najszybszych wzrostów wartości danego pola skalarnego w poszczególnych punktach, przy czym moduł (długość) każdej wartości wektorowej jest równy szybkości wzrostu. Wektor przeciwny do gradientu nazywa się często antygradientem.

Uogólnieniem gradientu na funkcje przestrzeni euklidesowej w inną jest macierz Jacobiego. Dalej idącym uogólnieniem na funkcje między przestrzeniami Banacha jest pochodna Frécheta.

Wprowadzenie

Na powyższych obrazkach pole skalarne jest czarno-białe, przy czym czerń reprezentuje wyższe wartości, a odpowiadającemu mu gradientowi odpowiadają niebieskie strzałki.

Przykładem może być pokój, w którym temperatura opisana jest polem skalarnym T. Tak więc w każdym punkcie (x,y,z) temperatura wynosi T(x,y,z) (zakładamy, że nie zmienia się ona w czasie). Wówczas w każdym punkcie pokoju gradient T w tym punkcie pokazuje kierunek (wraz ze zwrotem), w którym temperatura rośnie najszybciej. Moduł gradientu wskazuje jak szybko rośnie temperatura w tym kierunku.

Innym przykładem może być powierzchnia, dla której H(x,y) oznacza wysokość nad poziomem morza w punkcie (x,y). Gradientem H w punkcie jest wektor wskazujący kierunek największego pochylenia w tym punkcie. Miara tego pochylenia jest dana jako moduł wektora gradientu.

Dzięki iloczynowi skalarnemu gradient można wykorzystać do mierzenia nie tylko tego jak pole skalarne zmienia się w kierunku największej zmiany, lecz także w innych kierunkach. Niech w przykładzie ze wzgórzem największe pochylenie zbocza wynosi 40%. Jeśli droga biegnie prosto pod górę, to największe pochylenie drogi również będzie wynosić 40%. Jeśli jednak droga biegnie wokół wzgórza pod pewnym kątem (względem wektora gradientu), to będzie miała mniejsze nachylenie. Przykładowo jeśli kąt między drogą a kierunkiem w górę, rzutowany na płaszczyznę poziomą, wynosi 60°, to największe nachylenie wzdłuż drogi będzie wynosić 20%, co jest równe 40% razy cosinus 60°.

Ta obserwacja może być wyrażona matematycznie w następujący sposób. Jeśli funkcja wysokości terenu H jest różniczkowalna, to gradient funkcji H pomnożony skalarnie przez wektor jednostkowy daje pochylenie terenu w kierunku tego wektora. Dokładniej, jeśli H jest różniczkowalna, to iloczyn skalarny gradientu H przez dany wektor jednostkowy jest równy pochodnej kierunkowej H w kierunku tego wektora jednostkowego.

Podobnie obrazuje się zmianę innych wielkości fizycznych takich jak: stężenie, współczynnik pH, gęstości ładunku elektrycznego, jasność, kolor itp. w określonej przestrzeni.

Definicja

Gradient funkcji f(x,y) = −(cos²x + cos²y)² przedstawiony jako pole wektorowe na dolnej płaszczyźnie.

Gradient (lub gradientowe pole wektorowe) funkcji skalarnej $f(x_1, \dots, x_n)$ oznaczany $\nabla f,$ gdzie $\nabla$ (nabla) to wektorowy operator różniczkowy nazywany nabla. Innym oznaczeniem gradientu f jest $\operatorname{grad}\; f.$

Gradient f definiuje się jako pole wektorowe o składowych będących pochodnymi cząstkowymi f, tzn.

$\nabla f = \left[\frac{\partial f}{\partial x_1}, \dots, \frac{\partial f}{\partial x_n}\right].$

Gradient jest wektorem kolumnowym, jednak bywa zapisywany jako wektor wierszowy. Jeżeli funkcja zależy także od parametru takiego jak czas, to zwykle gradient oznacza wtedy wektor jej pochodnych przestrzennych.

Gradient funkcji wektorowej f = (f₁,f₂,f₃) to

$\nabla \mathrm f = \frac{\partial f_j}{\partial x_i} \mathbf e_i \mathbf e_j$

lub też transpozycja macierzy Jacobiego

$\frac{\partial (f_1, f_2, f_3)}{\partial (x_1, x_2, x_3)}.$

Jest to tensor drugiego rzędu.

Ogólniej gradient może być zdefiniowany za pomocą pochodnej zewnętrznej:

$\nabla \mathrm f = (\operatorname d\mathrm f)^\sharp.$

Symbole $\scriptstyle\flat$ oraz $\scriptstyle\sharp$ oznaczają tutaj izomorfizmy muzyczne.

Postać w trójwymiarowej przestrzeni współrzędnych

Postać gradientu zależy od użytego układu współrzędnych. W układzie:

• współrzędnych kartezjańskich ma postać

  $\nabla f(x, y, z) = \left[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right],$

• współrzędnych walcowych zapisuje się jako

  $\nabla f(r, \theta, z) = \left[\frac{\partial f}{\partial r}, \frac{1}{r} \frac{\partial f}{\partial \theta}, \frac{\partial f}{\partial z} \right],$

• współrzędnych sferycznych dany jest wzorem

  $\nabla f(r, \theta, \varphi) = \left[\frac{\partial f}{\partial r}, \frac{1}{r} \frac{\partial f}{\partial \theta}, \frac{1}{r \sin \theta} \frac{\partial f}{\partial \varphi} \right].$

Jeśli oznaczyć przez $\mathbf e_x, \mathbf e_y, \mathbf e_z$ wersory osi układu współrzędnych kartezjańskich, to gradient można zadać jako

$\frac{\partial f}{\partial x} \mathbf e_x + \frac{\partial f}{\partial y} \mathbf e_y + \frac{\partial f}{\partial z} \mathbf e_z.$

Podobnie ma się rzecz dla innych układów współrzędnych.

Przykład

Gradientem funkcji

f(x,y,z) = 2x + 3y² − sin z

we współrzędnych kartezjańskich jest

$\nabla f = \left[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right] = [2, 6y, -\cos z].$

Związek z pochodną i różniczką

Przybliżenie liniowe funkcji

Gradient funkcji f przestrzeni euklidesowej $\mathbb R^n$ w prostą euklidesową $\mathbb R$ w dowolnym punkcie p należącym do $\mathbb R^n$ charakteryzuje najlepsze przybliżenie liniowe f w punkcie p. Rozumie się przez to

$f(\mathrm x) \approx f(\mathrm p) + \nabla f(\mathrm p) \cdot (\mathrm x - \mathrm p)$

dla x bliskiego p, gdzie $\nabla f(\mathrm p)$ oznacza gradient f obliczony w punkcie p, a kropka to iloczyn skalarny na $\mathbb R^n.$ Równanie to jest równoważne dwóm pierwszym wyrazom rozwinięcia szeregu Taylora wielu zmiennych dla f w punkcie p.

Różniczka i pochodna (zewnętrzna)

Najlepszym przybliżeniem liniowym funkcji $f\colon \mathbb R^n \to \mathbb R$ w punkcie x należącym do $\mathbb R^n$ jest przekształcenie liniowe $\mathbb R^n \to \mathbb R$ oznaczane często $\operatorname df(\mathrm x)$ lub $\operatorname Df(\mathrm x)$ i nazywane różniczką bądź pochodną zupełną funkcji f w punkcie x. Stąd gradient związany jest różniczką następującym wzorem $\nabla f(\mathrm x) \cdot \mathbf v = \operatorname df(\mathrm x)(\mathbf v)$ dla dowolnego $\mathbf v \in \mathbb R^n.$ Funkcja $\operatorname df,$ która przekształca x na $\operatorname df(\mathrm x),$ nazywa się różniczką lub pochodną zewnętrzną f. Jest to przykład 1-formy różniczkowej.

Jeśli postrzegać $\mathbb R^n$ jako przestrzeń wektorów kolumnowych o n składowych rzeczywistych, to $\operatorname df$ można uważać za wektor wierszowy

$\operatorname df = \left[\frac{\partial f}{\partial x_1}, \dots, \frac{\partial f}{\partial x_n}\right]$

tak, iż $\operatorname df(\mathrm x)(\mathbf v)$ jest dana poprzez mnożenie macierzy. Gradient jest wówczas odpowiadającym mu wektorem kolumnowym, tzn. $\nabla f = (\operatorname df)^\operatorname T.$

Gradient jako pochodna

Niech U będzie zbiorem otwartym w $\mathbb R^n.$ Jeśli funkcja $f\colon U \to \mathbb R$ jest różniczkowalna (w sensie Frécheta), to różniczką f jest pochodna Frécheta f. Stąd $\nabla f$ jest funkcją z U w $\mathbb R$ taką, że

$\lim_{\mathbf u \to 0} \frac{|f(\mathrm x + \mathbf u) - f(\mathrm x) - \nabla f(\mathrm x) \cdot \mathbf u|}{\|\mathbf u\|} = 0,$

gdzie $\cdot$ oznacza iloczyn skalarny.

Stąd gradient spełnia standardowe własności pochodnej:

Liniowość

Gradient jest liniowy w tym sensie, iż jeżeli f i g są dwiema funkcjami o wartościach rzeczywistych różniczkowalnymi w punkcie $\mathrm a \in \mathbb R^n,$ zaś α i β są dwoma skalarami (stałymi rzeczywistymi), to kombinacja liniowa αf + βg jest różniczkowalna w a i co więcej:

$\nabla\left(\alpha f + \beta g\right)(\mathrm a) = \alpha \nabla f(\mathrm a) + \beta\nabla g(\mathrm a).$

Reguła iloczynu

Niech f i g są dwiema funkcjami o wartościach rzeczywistych różniczkowalnymi w punkcie $\mathrm a \in \mathbb R^n,$ wówczas reguła iloczynu zapewnia, że iloczyn (fg)(x) = f(x)g(x) funkcji f i g jest różniczkowalny w a oraz

$\nabla(fg)(\mathrm a) = f(\mathrm a) \nabla g(\mathrm a) + g(\mathrm a) \nabla f(\mathrm a).$

Reguła łańcuchowa

Niech $f\colon A \to \mathbb R$ będzie funkcją o wartościach rzeczywistych określoną na podzbiorze A przestrzeni $\mathbb R^n,$ różniczkowalną w punkcie a. Istnieją dwie postaci reguły łańcuchowej związanej z gradientem. Wpierw niech g oznacza krzywą parametryczną, tj. funkcję $g\colon I \to \mathbb R^n$ odwzorowującą podzbiór $I \subseteq \mathbb R$ w $\mathbb R^n.$ Jeśli g jest różniczkowalna w punkcie $\mathrm c \in I$ takim, że g(c) = a, to

$(f \circ g)'(\mathrm c) = \nabla f(\mathrm a) \cdot g'(\mathrm c).$

Ogólniej, jeśli jest $I \subseteq \mathbb R^k,$ to prawdziwa jest równość:

$\mathbf J_{\mathrm f \circ \mathrm g}(\mathrm c) = \bigl(\mathbf J_\mathrm g(\mathrm c)\bigr)^\operatorname T \nabla f(\mathrm a),$

gdzie $\mathbf J_\mathrm f(\mathrm c)$ oznacza macierz Jacobiego, zaś $\cdot^\operatorname T$ oznacza transpozycję macierzy.

Drugą postać reguły łańcuchowej można przedstawić następująco: niech $h\colon I \to \mathbb R$ bedzie funkcją o wartościach rzeczywistych określoną na podzbiorze I prostej $\mathbb R,$ przy czym h jest różniczkowalna w punkcie $c = f(\mathrm a) \in I.$ Wówczas

$\nabla(h \circ f)(\mathrm a) = h'(c) \nabla f(\mathrm a).$

Własności przekształceń

Choć gradient jest zdefiniowany za pomocą współrzędnych, to jest on kontrawariantny ze względu na przekształcenie współrzędnych za pomocą macierzy ortogonalnej. Jest to prawda w tym sensie, że jeżeli $\mathbf A$ jest macierzą ortogonalną, to

$\nabla(f(\mathbf A\mathrm x)) = \mathbf A^\operatorname T \nabla f(\mathbf A\mathrm x) = \mathbf A^{-1} \nabla f(\mathbf A\mathrm x),$

co wynika z opisanej wyżej reguły łańcuchowej. Wektor zachowujący się w ten sposób nazywa się wektorem kontrawariantnym, gradient jest zatem szczególnym rodzajem tensora.

Różniczka jest naturalniejsza od gradientu, gdyż jest niezmiennicza na wszystkie przekształcenia współrzędnych (dyfeomorfizmy), podczas gdy gradient jest niezmienniczy tylko na przekztałcenia ortogonalne (ze względu na jawne użycie iloczynu skalarnego w definicji). Z tego powodu często rozmywa się różnicę między tymi dwoma pojęciami korzystając z pojęcia wektorów kowariantnych i kontrawariantnych. Z tego punktu widzenia składowe gradientu przekształcane są kowariantnie przy zmianie współrzędnych, dlatego mówi się o kowariantnym polu wektorowym, podczas gdy składowe pola wektorowego w zwykłym sensie zmieniają się kontrawariantnie. W języku tym gradient jest więc różniczką, jako że kowariantne pole wektorowe jest tym samym, co 1-forma różniczkowa.

Dalsze własności i zastosowania

Poziomice

Dla funkcji f określonej w punkcie p można rozważać powierzchnię przez niego przechodzącą, w punktach której funkcja przyjmuje wszędzie tę samą wartość. Powierzchnię taką nazywa się wówczas powierzchnią poziomicy.

Jeśli pochodne cząstkowe f są ciągłe, to iloczyn skalarny $\nabla f(\mathrm x) \cdot \mathbf v$ gradientu w punkcie x i wektora $\mathbf v$ daje pochodną kierunkową f w punkcie x wzdłuż $\mathbf v.$ Wynika stąd, że w tym przypadku gradient f jest ortogonalny do poziomic f. Przykładowo powerzchnia poziomicy w przestrzeni trójwymiarowej jest określona równaniem postaci F(x,y,z) = c. Gradient F jest wtedy wektorem normalnym do powierzchni.

Ogólniej, dowolna hiperpowierzchnia zanurzona w rozmaitości riemannowskiej może być opisana równaniem postaci F(p) = 0, gdzie $\operatorname dF$ nigdzie nie znika. Gradient F jest wtedy normalny do tej hiperpowierzchni.

Rozmaitości riemannowskie

Dla dowolnej funkcji gładkiej f określonej na rozmaitości riemannowskiej (M,g), gradient f to pole wektorowe $\nabla f$ takie, że dla dowolnego pola wektorowego X zachodzi

$g(\nabla f, X) = \partial_X f$, tzn. $g_x\bigl((\nabla f)_x, X_x\bigr) = (\partial_X f)(x)$,

gdzie $g_x(\cdot, \cdot)$ to iloczyn wewnętrzny wektorów stycznych w punkcie x wyznaczony przez metrykę g, symbol $(\nabla f)_x$ oznacza gradient f obliczony w punkcie x, zaś $\partial_X f$, oznaczane czasami X(f) jest funkcją, która każdemu punktowi $x \in M$ przyporządkowuje pochodną kierunkową f w kierunku X obliczoną w punkcie x. Innymi słowy $(\partial_X f)(x)$, opisana za pomocą mapy φ z otwartego podzbioru M w podzbiór otwarty $\mathbb R^n$, jest dana wzorem:

$\sum_{j=1}^n X^j\bigl(\varphi(x)\bigr) \frac{\partial}{\partial x_j}(f \circ \varphi^{-1}) \Big|_{\varphi(x)}$,

gdzie X^j oznacza j-tą składową X w tej mapie.

Tak więc lokalnie gradient przyjmuje postać:

$\nabla f = g^{ik}\frac{\partial f}{\partial x^k} \frac{\partial}{\partial x^i}.$

Uogólniając przypadek $M = \mathbb R^n$ gradient funkcji jest związany z pochodną zewnętrzną, gdyż $(\partial_X f)(x) = \operatorname df_x(X_x)$, gdzie $\operatorname df_x$ to pochodna f w punkcie x. Dokładniej, gradient $\nabla f$ jest polem wektorowym związanym z 1-formą różniczkową $\operatorname df$ za pomocą izomorfizmu muzycznego $\sharp = \sharp^g\colon \operatorname T^*M \to \operatorname TM$ (nazywanego „krzyżykiem”) określonego za pomocą metryki g. Związek między pochodną zewnętrzną a gradientem funkcji $\mathbb R^n$ jest przypadkiem szczególnym powyższego, gdy metryka jest płaską metryką daną za pomocą (euklidesowego) iloczynu skalarnego.

Nauki przyrodnicze

• W niektórych szybko przebiegających reakcjach chemicznych zachodzących na granicy faz zachodzi zjawisko gradientowego stężenia substratów w objętości. Stwierdzenie to oznacza, że blisko granicy faz, gdzie przebiega właściwa reakcja stężenie produktów jest najwyższe, zaś czym dalej od tej granicy stężenie to spada. Zjawisko takie zachodzi np. przy elektrolizie.
• W przypadku polimerów możliwe jest otrzymywanie tzw. kopolimerów gradientowych, w których na jednym końcu polimeru występuje więcej jednego, a na przeciwległym drugiego meru.
• W meteorologii fragment opisu stanu atmosfery „W niezbyt grubej warstwie –81 m, różnica temperatury wynosiła aż 8,5°C, tj. średnio ponad jeden stopień na 10 m wysokości. Tak duże ujemne, pionowe gradienty temperatury są rzadkością”.
• W fizyce gradientem energii potencjalnej jest siła, a potencjału (np. elektrycznego, grawitacyjnego) jest natężenie tego pola.
• W optymalizacji występują metody umożliwiające wyznaczenie ekstremów funkcji wielu zmiennych: metoda gradientu prostego, metoda gradientu sprzężonego, metoda najszybszego spadku, metoda Newtona, algorytm Levenberga-Marquardta.

Linki zewnętrzne

• L. P. Kuptsov: Gradient (ang.). 2001.
• Weisstein, Eric W., „Gradient” na MathWorld.

Bibliografia

• Theresa M. Korn, Granino Arthur Korn: Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. Nowy Jork: Dover Publications, 2000, s. 157–160. ISBN 0-486-41147-8. OCLC 43864234. 
• H. M. Schey: Div, Grad, Curl, and All That. Wyd. II. W. W. Norton, 1992. ISBN 0-393-96251-2. OCLC 25048561.