Funkcja "na"

W surjekcji każdemu elementowi przeciwdziedziny odpowiada co najmniej jeden element dziedziny

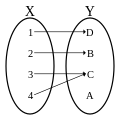
Funkcja „na” a. surjekcja pisane też czasami jako suriekcja – funkcja przyjmująca jako swoje wartości wszystkie elementy przeciwdziedziny, tj. której obraz jest równy przeciwdziedzinie.

Definicja

Niech $X$ oraz $Y$ będą dowolnymi zbiorami. Funkcja $f\colon X \to Y$ odwzorowuje zbiór $X$ na zbiór $Y$ wtedy i tylko wtedy, gdy każdy element zbioru $Y$ jest wartością funkcji w pewnym punkcie,

$\forall{y \in Y}\; \exists{x \in X}\; f(x) = y,$

co oznacza się często jako $f\colon X \xrightarrow{na} Y$ lub $f\colon X \xrightarrow[na]\ Y.$

Warunkiem równoważnym jest pokrywanie się przeciwdziedziny z obrazem dziedziny, $f(X) = Y,$ inaczej $\operatorname{Im} f = Y.$

Uwaga

Należy pamiętać, że to wybór przeciwdziedziny decyduje o surjektywności lub jej braku. Przyjrzyjmy się następującym funkcjom:

$f_1\colon \mathbb R \to \mathbb R$ określonej wzorem $f_1(x) = x^2$ oraz

$f_2\colon \mathbb R \to [0, \infty)$ określonej wzorem $f_2(x) = x^2$.

Tylko druga z powyższych funkcji jest surjekcją, mimo że są one określone tym samym wzorem.

Zauważmy ponadto, że dowolna funkcja jest surjekcją, jeśli jako zbiór $Y$ przyjmiemy zbiór jej wartości.

Przykłady

Niech $x \in \mathbb R$ będzie zmienną rzeczywistą, wówczas poniższe funkcje są surjekcjami:

• $f\colon x \mapsto \tfrac{1}{x}$ dla $x \ne 0$ na $\mathbb R \setminus \{0\}$,
• $f\colon x \mapsto x^a$ dla $a \in \{2n+1\colon n \in \mathbb N\}$ na $\mathbb R$,
• $f\colon x \mapsto \ln x$ dla $\ x > 0$ na $\mathbb R$,
• $f\colon x \mapsto \operatorname{tg}\;x$ dla $x \in \bigcup\{(-\tfrac{\pi}{2} + k\pi, \tfrac{\pi}{2} + k\pi) \colon k \in \mathbb Z \}$ na $\mathbb R$,
• $f\colon \mathbb R \overset\underset\mathrm{na}\ \to \mathbb Z, \quad f(x) = \lceil x \rceil$,
• $f\colon \mathbb R \overset\underset\mathrm{na}\ \to \{1\}, \quad f(x) = 1$.

Pisownia

Słowo surjekcja tradycyjnie bywa pisane przez j, tę wersję jako jedyną dopuszczalną podaje słownik języka polskiego PWN . Zasady pisowni polskiej w ogólnych przypadkach nakazują jednak stosowanie j po innych spółgłoskach niż c, s i z w wypadku, gdy przedrostek jest zakończony spółgłoską, a rdzeń zaczyna się od j; np. podjazd, nadjechał, zjawa czy rozjaśnić. W pozostałych wypadkach pisze się i. Z tego powodu dopuszczalna i przez niektórych stosowana jest pisownia suriekcja i iniekcja przez i. Jest to jednak termin fachowy, pochodzenia obcego, gdzie można stosować inne reguły i matematycy przeważnie używają pisowni surjekcja oraz injekcja przez j. Językoznawcy często uznają uzus obowiązujący wśród specjalistów posługujących się tym pojęciem. Oni zaś stosują obydwie formy, zarówno surjekcja (częściej), jak i suriekcja.

Zobacz też

• funkcja "w"
• funkcja różnowartościowa (iniekcja)
• funkcja wzajemnie jednoznaczna (bijekcja)
• epimorfizm

Bibliografia

• Marian Gewert, Zbigniew Skoczylas: Analiza matematyczna 1 : definicje, twierdzenia, wzory. Wyd. XI zmienione. Wrocław: Oficyna Wydawnicza GiS, 2001, s. 18. ISBN 83-85941-82-7.