Całka Lebesgue’a
Całka Lebesgue’a – konstrukcja matematyczna rozszerzająca pojęcie całki Riemanna na szerszą klasę funkcji, wprowadzona w 1902 r. przez francuskiego matematyka Henriego Lebesgue’a[1]. Rozszerzenie dotyczy także dziedziny, na której mogą być określone funkcje podcałkowe.
Sam Lebesgue tak porównywał swoją definicję z klasyczną całką Riemanna[potrzebny przypis]:
- Wyobraźcie sobie, że należy zapłacić pewną sumę. Można w tym celu wyciągać pieniądze z portmonetki po kolei, aby uzbierać potrzebną kwotę. To całka Riemanna. Można też wyjąć wszystkie monety naraz, posegregować je według wartości i dopiero teraz zapłacić kilkoma monetami. To moja całka.
Wyjaśnić można to następująco: w metodzie Riemanna przebiega się dziedzinę funkcji i mierzy „wysokość” wykresu po kolei w każdym miejscu, podczas gdy metoda Lebesgue’a bierze pod uwagę najpierw zbiór wartości funkcji i stosownie do tego wybiera kawałki dziedziny.
Jeżeli dla danej funkcji istnieje całka Riemanna, to jest ona równa całce Lebesgue’a tej funkcji. Zasadnicza przewaga całki Lebesgue’a polega na tym, że współgra z pojęciem granicy punktowej ciągu funkcji i w opisie matematycznym można zamieniać kolejność operacji liczenia całki i granicy (nie jest to zawsze możliwe w przypadku całki Riemanna). Obecnie całka Lebesgue’a jest jednym z podstawowych narzędzi współczesnej matematyki i nauk ją wykorzystujących.
Całka Riemanna jest konstrukcją związaną nierozerwalnie z przestrzeniami euklidesowymi; uogólnienie Lebesgue’a umożliwia całkowanie funkcji określonych na ogólniejszych przestrzeniach z miarą. Niżej naszkicowane podejście jest jednym z wielu możliwych.
Wprowadzenie[edytuj | edytuj kod]

Całka Riemanna jest związana z miarą Jordana, która jest tylko skończenie addytywną funkcją zbioru. Innymi słowy zakłada się, że miara sumy skończonej liczby zbiorów rozłącznych jest równa sumie miar poszczególnych zbiorów. Jednym z podstawowych kroków na drodze ku rozszerzeniu pojęcia całki Riemanna na funkcje typu funkcji Dirichleta było zastąpienie miary Jordana miarą Lebesgue’a, która jest już przeliczalnie addytywna, tzn. taka, że własność sumowania zachodzi także dla nieskończonej ilości zbiorów rozłącznych (zgodnie z tą obserwacją generalizacji uległo także ogólne pojęcie miary).
Definicja całki związanej z miarą Lebesgue’a wymaga zmiany spojrzenia na proces mierzenia obszaru. W definicji całki Riemanna dziedzina funkcji jest dzielona na krótkie przedziały. Tymczasem przy obliczaniu całki Lebesgue’a to nie dziedzina, ale przeciwdziedzina całkowanej funkcji jest dzielona na skończenie wiele przedziałów.
Dla ułatwienia opisu założone zostanie, iż przeciwdziedzina dodatniej funkcji jest zawarta w przedziale Aby znaleźć przybliżenie wartości pola obszaru pod wykresem funkcji należy podzielić przedział na rozłączne podprzedziały o końcach w punktach
Jeżeli przyjąć (por. rysunek) i wybrać liczby (na rysunku liczby te znajdują się na wysokości czerwonych odcinków), to każdy z obszarów ma pole, które równe jest mierze zbioru pomnożonej przez Otrzymane w ten sposób obszary są parami rozłączne, można zatem oczekiwać, że suma ich pól będzie dobrym przybliżeniem do pola obszaru pod funkcją – tym lepszym, im drobniejszy był początkowy podział zbioru wartości za pomocą liczb Ściśle podejście to realizuje się poprzez przybliżanie zadanej funkcji funkcjami prostymi, czyli takimi, które mają tylko skończenie wiele wartości przyjmowanych na mierzalnych podzbiorach dziedziny.
Konstrukcja[edytuj | edytuj kod]
Oznaczenia[edytuj | edytuj kod]
Dalej stosowana będzie następująca konwencja skracająca zapis: symbole
oznaczać będą odpowiednie relacje, tzn.
dla wszystkich elementów należących do ustalonego zbioru lub też całej dziedziny, jeśli nie zostanie zaznaczone inaczej. Podobnie będzie miała się rzecz z funkcjami (minimum i maksimum) i im podobnymi.
Całkę Lebesgue’a wprowadza się zwykle wraz z miarą Lebesgue’a jako uogólnienie całki Riemanna w przestrzeniach euklidesowych. Jednak wybór miary zależy od zastosowań, sama zaś konstrukcja obowiązuje dla szerszej klasy przestrzeni. Z tego powodu wszędzie, gdzie będzie to można zrobić bez szkody dla jasności wywodu oznaczenie miary przy całce, tzn. będzie konsekwentnie pomijane:
co wydatnie wpłynie na przejrzystość wzorów. Na podobnej zasadzie opuszczane będzie też wskazanie miary w przy mierzalności zbiorów, czy funkcji (zob. niżej).
Funkcje mierzalne[edytuj | edytuj kod]
Niech dana będzie przestrzeń z miarą Elementy σ-ciała określonego na przestrzeni nazywa się zbiorami -mierzalnymi względem
Funkcja jest -mierzalna, jeśli -mierzalny jest przeciwobraz przedziału dla dowolnego Wówczas także mierzalne są przeciwobrazy dowolnych zbiorów borelowskich.
Zbiór funkcji mierzalnych jest zamknięty ze względu na działania algebraiczne. W szczególności jeżeli mierzalne są funkcje to mierzalne są także suma, różnica, iloczyn oraz iloraz tych funkcji, tj.
- oraz (w ostatnim przypadku: iloraz określony tam, gdzie ma to sens).
Ponadto mierzalne są funkcje:
oraz
nazywane odpowiednio częścią dodatnią oraz ujemną funkcji (moduł, części dodatnia i ujemna są funkcjami nieujemnymi). Wprost z definicji wynika, że:
- oraz
Zbiór funkcji mierzalnych jest zamknięty ze względu na branie granic punktowych, tzn. jeżeli mierzalne są funkcje należące do ciągu to mierzalne są również funkcje
Funkcje proste[edytuj | edytuj kod]
Funkcję nazywa się prostą, jeżeli jej obraz jest zbiorem skończonym, zaś każda jej wartość przyjmowana jest na pewnym zbiorze mierzalnym tzn. dla Innymi słowy funkcję nazywa się prostą, jeżeli można przedstawić ją w postaci skończonej kombinacji liniowej funkcji charakterystycznych (indykatorów) zbiorów mierzalnych:
dla pewnych wartości oraz zbiorów
Całka Lebesgue’a[edytuj | edytuj kod]
Konstrukcja całki Lebesgue’a polega na stopniowym komplikowaniu klasy funkcji całkowalnych poczynając od najprostszych.
- Funkcje charakterystyczne
Jedyną rozsądną możliwością przypisania wartości całce z funkcji charakterystycznej zbioru mierzalnego jest miara tego zbioru:
Wynik może być równy o ile nie jest miarą skończoną.
- Funkcje proste
Jeżeli jest nieujemną funkcją prostą (kombinacją liniową funkcji charakterystycznych), to całkę Lebesgue’a tej funkcji definiuje się wzorem
Całkę Lebesgue’a z dowolnej funkcji prostej definiuje się jako
o ile skończona jest przynajmniej jedna z odejmowanych tu całek. Funkcja jest całkowalna, jeśli obie te całki są skończone.
- Funkcje mierzalne
Całkę Lebesgue’a nieujemnej funkcji mierzalnej określa się jako
- jest nieujemną funkcją prostą taką, że
Definicja całki Lebesgue’a z funkcji mierzalnej nie różni się wiele od definicji całki z dowolnej funkcji prostej:
gdy skończona jest przynajmniej jedna z odejmowanych tu całek. Podobnie jak wyżej jest całkowalna, gdy obie te całki są skończone.
- Zbiory mierzalne
Całkę z funkcji mierzalnej na zbiorze mierzalnym określa się jako
gdzie oznacza funkcję charakterystyczną zbioru
Własności i podstawowe twierdzenia[edytuj | edytuj kod]
Niech dana będzie przestrzeń z miarą zaś
Całka Lebesgue „nie odróżnia” funkcji różniących się na zbiorach miary zero. Precyzyjniej: funkcje i są sobie równe prawie wszędzie (p.w.), jeżeli
Dlatego jeśli są nieujemnymi funkcjami mierzalnymi (przyjmującymi być może nieskończoność) takimi, że prawie wszędzie, to
Jeżeli są równe sobie prawie wszędzie, to funkcja jest całkowalna wtedy i tylko wtedy, gdy całkowalna jest funkcja a ich całki są sobie równe.
Do najprostszych własności całki Lebesgue’a można zaliczyć poniższe:
- jeżeli jest mierzalna i równa zero poza zbiorem miary zerowej, to jest ona całkowalna oraz
- jeśli jest mierzalna i ograniczona na oraz to jest całkowalna na dodatkowo jeżeli to
- jeżeli jest mierzalna, a całkowalna, oraz prawie wszędzie, to także jest całkowalna; ponadto
Całka Lebesgue’a ma ponadto następujące ważne własności:
Jeśli są całkowalne, to ich kombinacja liniowa również jest całkowalna dla dowolnych rzeczywistych przy czym
Jeżeli są całkowalne oraz to
Niech będzie ciągiem nieujemnych funkcji mierzalnych takich, że dla każdego Wówczas
Uwaga: wartość dowolnej z powyższych całek może być nieskończona.
Jeżeli jest ciągiem nieujemnych funkcji mierzalnych, to
Raz jeszcze wartość dowolnej z całek może być nieskończona.
Jeżeli jest ciągiem zespolonych funkcji mierzalnych o granicy punktowej i jeśli istnieje taka funkcja całkowalna że dla każdego to jest całkowalna oraz
- Podstawowe twierdzenie rachunku całkowego na prostej
Jeżeli funkcja jest całkowalna w sensie Lebesgue’a na przedziale oraz funkcja jest określona przez to jest różniczkowalna prawie wszędzie, a jej pochodna jest prawie wszędzie (tzn. poza zbiorem miary zero) równa Na odwrót, jeżeli funkcja jest różniczkowalna w przedziale a jej pochodna jest ograniczona w przedziale to jest całkowalna w sensie Lebesgue’a i prawdziwy jest wzór
Przykłady[edytuj | edytuj kod]
Typowym przykładem przewagi całki Lebesgue’a nad całką Riemanna jest funkcja Dirichleta, tzn. funkcja charakterystyczna zbioru liczb wymiernych, czyli funkcja
Zbiór liczb wymiernych jest przeliczalny, poza nim zaś funkcja ta jest stale równa zeru. Dlatego naturalnym jest więc oczekiwanie, że całka tej funkcji („pole pod wykresem”) powinna być równa zeru, w szczególności powinna istnieć sama całka (możliwość „zmierzenia” wspomnianego pola).
Całkowanie Riemanna nie daje sensownego wyniku, w teorii Lebesgue’a jest to natomiast zwykła funkcja prosta, która przyjmuje tylko dwie wartości (0 i 1), tyle że w dość „nieregularny” sposób. Całka Lebesgue’a funkcji wynosi
gdyż miara zbioru liczb wymiernych wynosi zero (co wynika wprost z definicji miary i przeliczalności zbioru liczb wymiernych). W tym przypadku, wychodząc od zbioru wartości, podzielono dziedzinę tylko na dwie części, przy czym żadna z nich nie była odcinkiem.
Istnieją również funkcje niecałkowalne w sensie Lebesgue’a. Całka
nie istnieje, czego można dowieść korzystając z twierdzenia Fubiniego.
Porównanie z całką Riemanna[edytuj | edytuj kod]
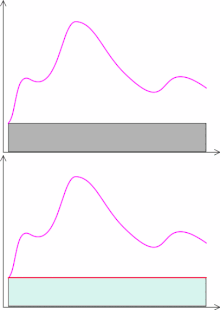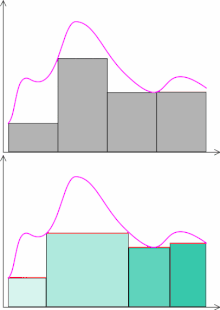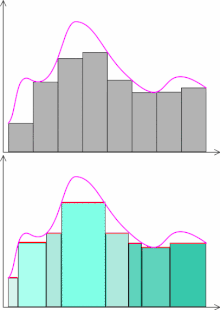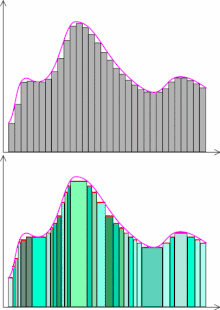
W przypadku całki Riemanna proces mierzenia tego pola jest oparty na dzieleniu dziedziny funkcji na przedziały. Podczas gdy metoda ta działa bardzo dobrze dla funkcji ciągłych, to funkcje których zbiór punktów nieciągłości nie jest miary zero, nie są całkowalne w sensie Riemanna. Co więcej, wśród tych niecałkowalnych znajdują się funkcje dość proste i często spotykane, a możliwość ich całkowania (włączenia do teorii całki) jest istotna zarówno dla teoretyków, jak i dla zastosowań.
Na rysunku obok pokazano poglądowe porównanie całek Riemanna i Lebesgue’a. W całce Riemanna podział na prostokąty pola pod wykresem jest z grubsza „dowolny”: dziedzinę dzieli się na drobne kawałki, w każdym „kawałku” wybiera pewną wysokość prostokąta (wysokością jest dowolna wartość funkcji na tym kawałku).
Typowym wyborem w praktyce jest podział równomierny na osi jak przedstawiono na górnym rysunku obok. W całce Lebesgue’a przybliża się daną funkcję niemalejącym ciągiem funkcji prostych. Jest to typowy sposób realizacji supremum użytego w jej definicji. Chociaż graficznie wygląda to na pierwszy rzut oka podobnie, to należy zauważyć, że podział na prostokąty jest „sterowany” zbiorem wartości funkcji prostej. Co więcej, wspomniane funkcje proste można wybierać dość dowolnie; typowy wybór w praktyce opiera się na analizie (podziale) zbioru wartości danej funkcji podcałkowej, tak jak to opisano to wcześniej. Skutkuje to podziałem dziedziny na kawałki, które nie są już koniecznie tylko odcinkami: jeden „kawałek” może być np. sumą kilku odcinków (na rysunku obok sumy takie zaznaczono wspólnym kolorem prostokąta). W ogólności, dla mniej regularnych funkcji taki „kawałek” może mieć bardzo skomplikowaną postać i aby go „zmierzyć” wprowadza się miarę Lebesgue’a.
Jeżeli funkcja podcałkowa jest dostatecznie regularna, np. ciągła, obie definicje dadzą ten sam rezultat. W przypadku mniej regularnych funkcji całka Riemanna może w ogóle nie istnieć (zob. powyższy przykład).
Wszystkie wzory na całkowanie funkcji podstawowych w sensie Riemmana przenoszą się na odpowiednie wzory dla całki w sensie Lebesgue’a. Obowiązuje również twierdzenie Fubiniego mówiące o możliwości zamiany całki podwójnej na iterowaną oraz zmianie kolejności obliczania tych całek. Jednak najważniejsze cechy całki Lebesgue’a są związane ze zgodnością pojęcia całki i granicy punktowej ciągu funkcji. Mówiąc najogólniej, przy odpowiednich warunkach całka z granicy ciągu funkcji jest równa granicy ciągu całek tych funkcji. Innymi słowy można zamieniać kolejność liczenia granicy ciągu i całki funkcji. Odpowiednie własności są ujęte precyzyjnie w następujących twierdzeniach:
- twierdzenie Lebesgue’a o zbieżności monotonicznej,
- twierdzenie Lebesgue’a o zbieżności ograniczonej,
- lemat Fatou.
Żadne z tych twierdzeń nie może być sformułowane w podobnie prosty sposób dla całki Riemanna, gdyż granica ciągu funkcji („regularnych”, prostych) może w ogóle nie być całkowalna w sensie Riemanna. To właśnie przede wszystkim ta zasadnicza różnica przyczyniła się do sukcesu pozornie bardziej skomplikowanej i odchodzącej od intuicyjnego pojęcia pola teorii Lebesgue’a.
Alternatywne sformułowania[edytuj | edytuj kod]
Całkę względem miary Lebesgue’a można określić nie odwołując się do całej skomplikowanej maszynerii teorii miary; jednym z takich podejść jest tzw. całka Daniella.
Istnieje również podejście do teorii całkowania poprzez metody analizy funkcjonalnej. Całka Riemanna istnieje dla dowolnej funkcji ciągłej o zwartym nośniku określonej na (lub ustalonym otwartym podzbiorze takiej przestrzeni). Całki ogólniejszych funkcji mogą być skonstruowane za pomocą wspomnianych całek. Otóż niech będzie przestrzenią wszystkich funkcji o wartościach rzeczywistych zmiennej rzeczywistej o zwartym nośniku. Definiuje się wówczas normę na wzorem
Wówczas staje się unormowaną przestrzenią liniową (w szczególności jest to przestrzeń metryczna). Wszystkie przestrzenie metryczne mają uzupełnienia Hausdorffa; niech będzie takim uzupełnieniem. Przestrzeń ta jest izomorficzna z przestrzenią ilorazową funkcji całkowalnych w sensie Lebesgue’a przez podprzestrzeń funkcji o zerowej całce. Co więcej całka Riemanna jest funkcjonałem jednostajnie ciągłym względem normy na która jest gęsta w Stąd ma dokładnie jedno rozszerzenie na całą przestrzeń Całka ta jest właśnie całką Lebesgue’a.
Podejście powyższe może być uogólnione; może ono służyć konstrukcji całki względem miary Radona na przestrzeniach lokalnie zwartych. Stosuje je m.in. Bourbaki (2004) (zob. miary Radona na przestrzeniach lokalnie zwartych).
Zobacz też[edytuj | edytuj kod]
Uwagi[edytuj | edytuj kod]
- ↑ W rachunku prawdopodobieństwa spotyka się również zapis postaci
Przypisy[edytuj | edytuj kod]
- ↑ całka Lebesgue’a, [w:] Encyklopedia PWN [dostęp 2021-10-04].
Bibliografia[edytuj | edytuj kod]
- Walter Rudin: Analiza rzeczywista i zespolona. Łódź: PWN, 1986.
- Ryszard Rudnicki: Wykłady z analizy matematycznej. PWN. ISBN 83-01-13554-9.
- G. B. Folland: Real Analysis: Modern Techniques and Their Applications. (ang.).
- Paul Halmos, P. R. Halmos: Measure Theory. Nowy Jork: D. Van Nostrand Company, 1950. (ang.).


![{\displaystyle [0,b].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14920f285e636d0a7730c9ab1fc1a15c0301cee8)

![{\displaystyle [0,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba22e25e8f8604f012c599a7d4962562c4bb3f02)

![{\displaystyle A_{i}=f^{-1}{\big (}(a_{i},a_{i+1}]{\big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23205ae4ad1ab0f17ac54577842f76d0dff44c50)

![{\displaystyle A_{i}\times [0,c_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625c8466f98187c00dfbca2cf34f93639885d8ef)






























































![{\displaystyle f(E)\subseteq [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788e4112ed3158c6f2c9eb56d85c64ea9fe97d4c)
















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle F\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/22aae183016ffbb759663208b693d6a28be4e69e)



![{\displaystyle [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842)















