Przekształcenie liniowe
| Ten artykuł należy dopracować |
Przekształcenie liniowe (homomorfizm liniowy[1], operator liniowy, odwzorowanie liniowe, transformacja liniowa) – w algebrze liniowej jest to funkcja między przestrzeniami liniowymi zachowująca ich działania w tym sensie, że (dokładna definicja – patrz niżej):
- odwzorowanie sumy wektorów z jednej przestrzeni w drugą jest równe sumie odwzorowań poszczególnych wektorów tej sumy,
- odwzorowanie iloczynu wektora przez skalar jest równe iloczynowi skalara przez odwzorowanie danego wektora.
Przekształcenie liniowe jest więc homomorfizmem przestrzeni liniowych.
Przekształcenia liniowe są najogólniejszymi funkcjami między przestrzeniami liniowymi, zachowującymi kombinacje liniowe wektorów. Przekształcenie liniowe m.in. przekształcają proste w proste lub punkt, przy czym prosta musi przechodzić przez punkt początkowy początek przestrzeni zwany wektorem zerowym.
W przypadku przestrzeni liniowych skończonego wymiaru z ustalonymi bazami przekształcenia liniowe opisuje się zwykle za pomocą macierzy (zob. wybór baz). Np. operacje odbicia/obrotu są operacjami liniowymi – reprezentują je macierz odbicia/macierz obrotu.
Przekształcenia liniowe znajdują zastosowanie m.in. w zagadnieniach linearyzacji czy aproksymacji liniowej.
Uwaga:
W większości wypadków słowa „funkcja”, „przekształcenie” i „odwzorowanie” są używane zamiennie. Jednak nie można używać terminu „funkcja liniowa” wymiennie z terminem „odwzorowanie liniowe” – termin funkcja liniowa jest zarezerwowany dla funkcji na płaszczyźnie opisującej prostą.
Definicja[edytuj | edytuj kod]
Niech oznacza pewne ciało (np. liczby rzeczywiste czy zespolone), a i będą przestrzeniami liniowymi nad tym ciałem. Funkcję nazywa się przekształceniem liniowym, jeżeli jest
- addytywna (zachowuje dodawanie wektorów),
- jednorodna (zachowuje mnożenie przez skalar),
Powyższe warunki można połączyć w jeden, równoważny z nimi warunek liniowości[2]:
Przykłady[edytuj | edytuj kod]
Odwzorowania nieliniowe[edytuj | edytuj kod]
- Dla liczb rzeczywistych odwzorowanie nie jest liniowe.
- Dla liczb rzeczywistych odwzorowanie nie jest liniowe (choć równanie jest równaniem liniowym według terminologii używanej w geometrii analitycznej).
Powyższe odwzorowania nie spełniają warunków addytywności.
Odwzorowania liniowe[edytuj | edytuj kod]
- Funkcje jednorodne są funkcjami liniowymi, np.
- funkcja stała (odwzorowanie w przestrzeń trywialną)
- funkcja tożsamościowa
- jednokładność
- Pochodna jest liniowa, gdzie jest funkcją różniczkowalną (np. funkcją rzeczywistą; funkcje różniczkowalne tworzą przestrzeń funkcyjną, która jest przestrzenią liniową).
- Operacja różniczkowania przyporządkowania funkcji różniczkowalnej jej funkcji pochodnej jest operacją liniową ze zbioru funkcji różniczkowalnych na zbiór wszystkich funkcji (funkcje różniczkowalne tworzą przestrzeń funkcyjną, która jest przestrzenią liniową).
- Operacja różniczkowania definiuje także operator liniowy na przestrzeni wszystkich funkcji gładkich (tj. różniczkowalnych dowolną liczbę razy).
- Całka oznaczona, określona na przedziale jest odwzorowaniem liniowym ze zbioru funkcji całkowalnych o wartościach rzeczywistych z przedziału na zbiór
- Całka nieoznaczona o ustalonym punkcie początkowym definiuje odwzorowanie liniowe ze zbioru funkcji całkowalnych na zbiorze na przestrzeń funkcji o wartościach rzeczywistych, różniczkowalnych na zbiorze
- Jeżeli jest macierzą o elementach rzeczywistych, to definiuje odwzorowanie liniowe ze zbioru do zbioru gdy przyporządkowuje wektorowi kolumnowemu wektor kolumnowy Odwrotnie, każde odwzorowanie liniowe pomiędzy przestrzeniami liniowymi skończonego wymiary może być reprezentowane za pomocą macierzy
- Operator liniowy przekształcenia Fouriera, który przyporządkowuje funkcji funkcję :
-
Przykładowa funkcja postaci jest odwzorowaniem liniowym: funkcja ta mnoży współrzędną przez a współrzędną pozostawia bez zmian.
-
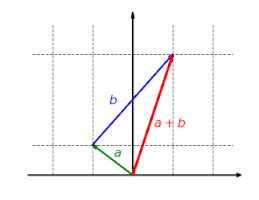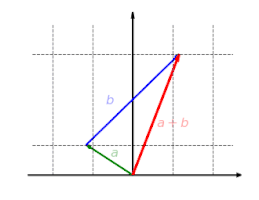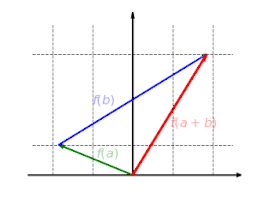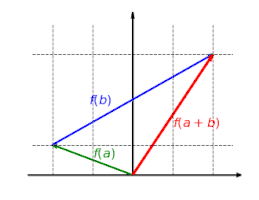
Funkcja liniowa jest zawsze addytywna, tzn. nie ma znaczenie, czy wektory są najpierw dodawane, a potem odwzorowywana ich suma, czy najpierw każdy z nich odwzorowywany, a potem są dodawane:
-
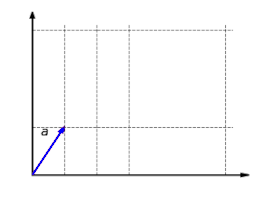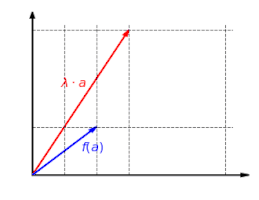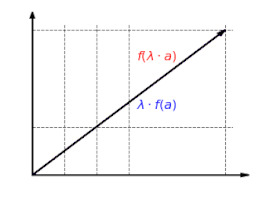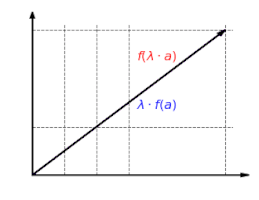
Funkcja liniowa jest zawsze jednorodna, tzn. nie ma znaczenia, czy wektor jest najpierw wydłużany, a potem odwzorowywany, czy najpierw odwzorowywany, a potem wydłużany:
Własności[edytuj | edytuj kod]
(1) Jeżeli funkcja spełnia dodatkowe warunki, np.
to odwzorowanie liniowe (homomorfizm) mające powyższe własności nazywa się odpowiednio
- monomorfizmem liniowym,
- epimorfizmem liniowym,
- izomorfizmem liniowym.
(2) Ponadto:
- przekształcenie liniowe przestrzeni w siebie nazywa się endomorfizmem,
- jeżeli jest ono dodatkowo odwracalne (jest izomorfizmem), to nazywa się je automorfizmem.
(3) Istnieje też szereg pojęć służących do opisu przekształceń liniowych i przestrzeni, na których są one określone. Definiuje się je za pomocą pojęć kombinacji liniowej, bazy i wymiaru, do najważniejszych należą:
- jądro, czyli przeciwobraz wektora zerowego (należy do każdej przestrzeni liniowej),
- rząd, definiowany jako wymiar obrazu całej przestrzeni.
Za ich pomocą można scharakteryzować każdy z powyższych rodzajów homomorfizmów:
- monomorfizm ma trywialne jądro (tj. złożone wyłącznie z wektora zerowego),
- epimorfizm ma pełny rząd (tzn. równy wymiarowi przeciwdziedziny),
- izomorfizm jest zarazem mono- jak i epimorfizmem.
(4) Twierdzenie Sylvestera o rzędzie: wymiar dziedziny jest równy sumie wymiarów obrazu i jądra przekształcenia[a]. Wynika stąd ważna obserwacja dotycząca izomorfizmów: wszystkie przestrzenie liniowe (nad ustalonym ciałem) równego wymiaru są izomorficzne, skąd wynika, iż wymiar jest niezmiennikiem izomorfizmów. Ponadto jeśli przekształcenie liniowe określone jest między dwoma przestrzeniami liniowymi równego, skończonego wymiaru, to z twierdzenia wynika, iż każdy monomorfizm czy epimorfizm jest izomorfizmem – innymi słowy w tym wypadku pojęcia mono-, epi- i izomorfizmu wynikają z siebie wzajemnie.
(5) Twierdzenie o wykresie charakteryzuje przekształcenia liniowe spośród wszystkich funkcji określonych między dwoma przestrzeniami liniowymi: odwzorowanie jest liniowe wtedy i tylko wtedy, gdy jej wykres, czyli zbiór par jest podprzestrzenią liniową przestrzeni (której wykres jest zawsze podzbiorem).
Pojęcia topologiczne czy analityczne, takie jak ciągłość czy różniczkowalność, nie przydają niczego w przypadku przestrzeni skończonego wymiaru – przekształcenia liniowe między nimi są ciągłe i gładkie na całej dziedzinie; sytuacja zmienia się diametralnie, jeśli rozpatruje się przestrzenie nieskończeniewymiarowe, zob. osobną sekcję.
Wybór baz[edytuj | edytuj kod]
Jeśli są przestrzeniami liniowymi skończonego wymiaru, to przekształcenie liniowe między nimi można przedstawić za pomocą macierzy przy czym:
- wybranie bazy w przestrzeni oraz bazy w przestrzeni prowadzi do wskazania izomorfizmów oraz w przestrzenie współrzędnych (które są przestrzeniami liniowymi)
- odwrotnie, każda macierz typu opisuje przekształcenie liniowe a dzięki wyborom baz również przekształcenie
Jeśli jest macierzą przekształcenia liniowego a macierz jednokolumnowa odpowiada wektorowi przestrzeni [b], to:
- działanie przekształcenia liniowego na wektor opisuje się jako mnożenie macierzy przez macierz jednokolumnowa tj.
- składaniu przekształceń liniowych odpowiada mnożenie odpowiadających im macierzy.
W ten sposób ogólna teoria macierzy może być wykorzystana do opisu przekształceń liniowych.
Istnieją jednak dwa zasadnicze powody, dla których rozpatruje się ogólne przekształcenia liniowe zamiast ich macierzy:
- w przestrzeniach liniowych nieskończonego wymiaru zapis za pomocą macierzy nie ułatwia przeprowadzania konkretnych rachunków, jak ma to miejsce w przypadku skończeniewymiarowym,
- istnieją własności, które łatwiej traktować w bardziej abstrakcyjny sposób, np. dowodząc, iż dana własność nie zależy od wyboru bazy; w szczególności dowodząc, iż istnieją przestrzenie, w których wybór bazy nie jest kanoniczny, tj. nie istnieje naturalny izomorfizm z przestrzenią współrzędnych (lub jej nieskończonym odpowiednikiem, zob. przykłady przestrzeni liniowych).
Endomorfizmy[edytuj | edytuj kod]
Zbiór wszystkich endomorfizmów przestrzeni tworzy pierścień nazywany po prostu pierścieniem endomorfizmów Do opisu endomorfizmów liniowych, nazywanych niekiedy „operatorami liniowymi”, na przestrzeniach skończonego wymiaru i ich macierzy kwadratowych stosuje się często pojęcia wyznacznika i śladu. Zwykle definiuje się je dla macierzy, dowodząc ich niezależności od wyboru bazy, możliwe jest jednak zdefiniowanie bez wyboru bazy dla przekształceń liniowych, jednak wtedy konieczne jest podanie przepisu na ich obliczenie – wyraża się ją wtedy za pomocą macierzy w ustalonej bazie – odzwierciedla to równoważność obu definicji. Niezmienniczość tych pojęć można tłumaczyć za pomocą podprzestrzeni niezmienniczych, w tym wektorów własnych i stowarzyszonych z nimi wartości własnych, które opisują kierunki zachowywane przez dane przekształcenie liniowe i stosunki jednokładności w tychże kierunkach: wyznacznik jest iloczynem wartości własnych, a ślad – ich sumą. Rząd jest wtedy równy liczbie niezerowych wartości własnych. Jeśli choć jedna wartość własna jest zerowa, to wyznacznik również jest zerowy – przekształcenie (lub macierz) nazywa się wtedy osobliwym (lub zdegenerowanym, a rząd nie jest pełny, skąd przekształcenie nie jest epimorfizmem). Dowodzi się, że osobliwość jest równoważna nieodwracalności.
- Twierdzenie o endomorfizmie
Jeśli jest przestrzenią liniową skończonego wymiaru, zaś oraz są wszystkimi, parami różnymi wartościami własnymi tego endomorfizmu, to następujące warunki są równoważne:
- jest endomorfizmem,
gdzie oznacza sumę prostą przestrzeni liniowych, a jest podprzestrzenią niezmienniczą stowarzyszoną z wartością własną endomorfizmu
Z powyższych uwag wynika, że wyznacznik, ślad i rząd są niezmiennikami endomorfizmów. Wszystkie te informacje zawarte są w wielomianie charakterystycznym przekształcenia (bądź macierzy): pierwiastkami tego wielomianu są wartości własne. Środki te okazują się niewystarczające w przypadku nieskończeniewymiarowym, gdzie pojęcia te mają odpowiednie uogólnienia (zob. Wymiar nieskończony).
Endomorfizm przestrzeni nazywa się
- redukowalnym, jeśli istnieje nietrywialna właściwa podprzestrzeń niezmiennicza endomorfizmu
- rozkładalnym, jeśli istnieją nietrywialne (właściwe) podprzestrzenie niezmiennicze endomorfizmu dla których suma prosta
- diagonalizowalnym, jeśli istnieją jednowymiarowe podprzestrzenie niezmiennicze endomorfizmu dla których suma prosta diagonalizacją nazywa się wybór tych podprzestrzeni.
Automorfizmy[edytuj | edytuj kod]
W ogólności automorfizmy liniowe, czyli odwracalne przekształcenie liniowe przestrzeni na siebie, opisują „symetrie” przestrzeni takie jak opisane wyżej (liniowe) zmiany bazy. Ponieważ złożenie automorfizmów jest automorfizmem, jest łączne z definicji, przekształcenie tożsamościowe jest automorfizmem, a dla każdego automorfizmu istnieje automorfizm do niego odwrotny, to zbiór automorfizmów przestrzeni tworzy grupę nazywaną ogólną lub pełną grupą liniową przestrzeni
Przestrzenie przekształceń[edytuj | edytuj kod]
Przekształcenia liniowe tworzą przestrzeń liniową z działaniami określonymi „punktowo”, tj. które wykonywane są dla każdego wektora w ten sam sposób:
oraz
Jeśli i to zgodnie z rozważaniami w sekcji Wybór baz każde przekształcenie jest izomorficzne z pewnym przekształceniem a co za tym idzie, z macierzą Oznacza to, że przestrzeń wszystkich przekształceń liniowych jest izomorficzna z przestrzenią która jest z kolei izomorficzna z przestrzenią macierzy typu Wynika stąd, że każda z tych przestrzeni ma (zachowywany przy izomorfizmach) wymiar Jeśli choć jedna z liczb jest nieskończona, to powyższa równość dalej pozostaje w mocy – wymiar przestrzeni przekształceń również jest wtedy nieskończony.
Wymiar nieskończony[edytuj | edytuj kod]
Bezpośrednim uogólnieniem przestrzeni współrzędnych na nieskończoną liczbę wymiarów jest nieskończona przestrzeń współrzędnych, w której tylko skończenie wiele współrzędnych jest różnych od zera, co umożliwia branie dowolnie długich, lecz mimo wszystko skończonych kombinacji liniowych; przykładem może być przestrzeń wielomianów jednej zmiennej (o współczynnikach z ustalonego ciała). Przekształcenia liniowe są określone w nich zupełnie analogicznie jak wyżej, jednak nie mają one swoich dobrych własności, np. endomorfizm przestrzeni nieskończonego wymiaru będący monomorfizmem nie musi być epimorfizmem (i na odwrót), przykładami są operatory przesunięcia czy określone w przestrzeni wielomianów przekształcenia pochodnej formalnej i antypochodnej formalnej (zob. wielomian – działania)[c]. Wynika to wprost z faktu, iż dla wzajemnie odwrotnych przekształceń liniowych określonych na skończeniewymiarowej przestrzeni liniowej warunek pociąga za sobą [d], który nie zachodzi w przypadku przestrzeni nieskończeniewymiarowych[e]. Podobnie w przestrzeniach skończonego wymiaru nie istnieją przekształcenia liniowe spełniające choć własność tę mają ww. operatory pochodnej formalnej czy przesunięcia (zob. komutator)[3].
Opisem przestrzeni liniowych nieskończonego wymiaru, które dodatkowo wyposażone są w jakąś strukturę umożliwiającą rozpatrywanie nieskończonych szeregów odpowiadających kombinacjom liniowym, zajmuje się dział matematyki nazywany analizą funkcjonalną. Klasyczna teoria dotyczy przestrzeni unormowanych, czyli przestrzeni liniowych ze zdefiniowanym pojęciem „długości” wektora (można w niej w naturalny sposób określić strukturę metryczną, czyli wprowadzić pojęcie „odległości”); aby zapewnić istnienie wektorów, dla których wspomniane szeregi są zbieżne zakłada się, że przestrzenie te są zupełne – przestrzenie takie nazywa się przestrzeniami Banacha. Z przyczyn historycznych przekształcenia liniowe zwykło nazywać się w analizie funkcjonalnej „operatorami liniowymi”, a formy liniowe – „funkcjonałami liniowymi” (skąd wziął swą nazwę sam dział).
Jeśli i są unormowanymi przestrzeniami liniowymi, to ograniczoność operatora definiuje się za pomocą warunku ograniczającego normę obrazu dowolnego wektora przez pewną wielokrotność normy tego wektora. Operator liniowy jest ograniczony wtedy i tylko wtedy, gdy jest ciągły (pojęcie to można zdefiniować w ogólniejszych przestrzeniach liniowo-topologicznych). W przestrzeniach Banacha ciągłość globalna jest równoważna ciągłości lokalnej, jak również przeprowadzaniu ciągów zbieżnych do zera w ciągi ograniczone. Rozpatrywanie operatorów ograniczonych i ciągłych w przestrzeniach skończonego wymiaru mija się z celem, gdyż wszystkie przekształcenia liniowe między nimi są ciągłe i ograniczone, co wynika z równoważności norm na tych przestrzeniach.
Wśród ważnych twierdzeń dotyczących przestrzeni nieskończonego wymiaru można wymienić twierdzenie Hahna-Banacha, twierdzenie Banacha-Steinhausa, twierdzenie o wykresie domkniętym czy twierdzenie o odwzorowaniu otwartym. Pojęcia wyznacznika i śladu uogólnia się na te przestrzenie pod postacią wyznacznika Fredholma i śladu funkcyjnego dla szczególnego rodzaju przekształceń, tzw. operatorów śladowych; innym rozszerzeniem jest wyznacznik funkcyjny. Wektory i wartości własne uogólniają się poprzez widmo (spektrum) operatora; diagonalizacji różnymi metodami odpowiadają wtedy różnorodne twierdzenia spektralne.
Uogólnienia[edytuj | edytuj kod]
Przekształcenia liniowe są homomorfizmami szczególnych struktur algebraicznych – przestrzeni liniowych, które z punktu widzenia algebry są modułami nad ciałem, podczas gdy w ogólności skalary modułów mogą należeć do ogólniejszej struktury nazywanej pierścieniem (tworzą go np. liczby całkowite). Wszystkie wyniki natury czysto algebraicznej niewykorzystujące liniowej niezależności są prawdziwe także w teorii modułów.
Przekształcenia liniowe można traktować jako przypadki szczególne innych przekształceń geometrycznych, najbliższym jej uogólnieniem jest przekształcenie afiniczne określane na przestrzeniach afinicznych; jego odpowiednikiem dla przestrzeni rzutowych jest przekształcenie rzutowe itd.
Zobacz też[edytuj | edytuj kod]
- przestrzeń ilorazowa, kojądro
- przekształcenie półliniowe, forma liniowa
- przekształcenie antyliniowe, forma półtoraliniowa
- przekształcenie dwuliniowe, forma dwuliniowa
- przekształcenie wieloliniowe, forma wieloliniowa
Uwagi[edytuj | edytuj kod]
- ↑ W istocie zachodzi więcej: dziedzina jest izomorficzna z sumą prostą obrazu i jądra.
- ↑ Macierz może być ona traktowana jako wektor współrzędnych, nazywany często wektorem kolumnowym, wektora wspomniana odpowiedniość jest izomorfizmem odpowiednich przestrzeni liniowych: przestrzeni macierzy jednokolumnowych i współrzędnych (zob. przestrzeń współrzędnych).
- ↑ Zdefiniowane są one przez swoje działanie na jednomianach (zob. twierdzenie o przekształceniu liniowym zadanym na bazie) wzorami oraz
- ↑ Skoro to co oznacza, że przekształcenie jest rzutem. Ponieważ wymiar obrazu nie przekracza większego z wymiarów obrazów przekształceń oraz rzut ten jest epimorfizmem, to przekształcenia również są epimorfizmami. Ponieważ na epimorfizmy określone na przestrzeniach skończonego wymiaru są monomorfizmami, to są monomorfizmami, skąd wynika, że rzut również jest monomorfizmem – jedynym takim jest przekształcenie tożsamościowe
- ↑ W przypadku danych odpowiednio jako pochodna oraz antypochodna formalna na przestrzeni wielomianów zachodzi jednakże jest równe zeru dla wielomianów stałych.
Przypisy[edytuj | edytuj kod]
- ↑ Andrzej Szczepański, Algebra liniowa z geometrią – Instytut Matematyki, s. 36, MFI UG, mat.ug.edu.pl, rok akademicki 2020/21 [dostęp 2021-08-18].
- ↑ Przekształcenie liniowe, [w:] Encyklopedia PWN [dostęp 2021-07-22].
- ↑ Algebra II – Wykład 1. [dostęp 2009-05-27].
Bibliografia[edytuj | edytuj kod]
- Linear operator, [w:] Encyklopedia of Mathematics [dostęp 2021-08-17].l