Funkcja ciągła

Funkcja ciągła – funkcja o następującej intuicyjnej własności: „mała” zmiana argumentu niesie ze sobą „małą” zmianę wartości; lub też: wartości funkcji dla „bliskich” sobie argumentów również będą sobie „bliskie”.

Funkcja rzeczywista zmiennej rzeczywistej (określona na całym zbiorze $\Bbb R$ lub jego podprzedziale, skończonym lub nie) może być postrzegana jako ciągła, jeżeli jej wykres można „narysować bez odrywania ołówka od papieru” (bez ograniczeń w czasie lub przestrzeni).

Funkcje rzeczywiste

Dla funkcji rzeczywistych zmiennej rzeczywistej istnieją dwie równoważne definicje ciągłości: jedna z nich podana przez Augustina Louisa Cauchy'ego, nazywana popularnie epsilonowo-deltową z racji przyjętych zwyczajowych oznaczeń; druga zaproponowana przez Heinricha Eduarda Heinego, nazywana też definicją ciągową. Niech $M \subseteq \mathbb R$ oraz $f\colon M \to \mathbb R$.

Definicja Cauchy'ego

Jeżeli $f$ spełnia dla ustalonego $x \in M$ warunek

$\forall_{\varepsilon > 0}\; \exists_{\delta > 0}\; \forall_{y \in M}\ \ \ |x-y| < \delta \implies |f(x) - f(y)| < \varepsilon$,

to jest ona ciągła w sensie Cauchy'ego w punkcie $x$. Jeżeli spełnia ona powyższy warunek dla każdego $x \in M$, czyli

$\forall_{x \in M}\; \forall_{\varepsilon > 0}\; \exists_{\delta > 0}\; \forall_{y \in M}\ \ \ |x-y| < \delta \implies |f(x) - f(y)| < \varepsilon$,

to mówimy, że jest ciągła (w sensie Cauchy'ego) na zbiorze $M$.

Definicja Heinego

Funkcja $f$ jest ciągła w sensie Heinego w punkcie $x \in M$, jeśli dla każdego ciągu $(x_n)$ liczb z $M$, który jest zbieżny do $x$ ciąg wartości $\big(f(x_n)\big)$ jest zbieżny do $f(x)$, czyli

$\forall_{x \in M}\ \ \ x_n \to x \Rightarrow f(x_n) \to f(x)$.

Uwagi

Warto zauważyć, że z obiema definicjami ciągłości funkcji w punkcie są związane odpowiednie definicje granicy funkcji w punkcie. Używając pojęcia granicy funkcji możemy powiedzieć, że funkcja $f$ jest ciągła w punkcie $x \in X$, gdy albo $x$ nie jest punktem skupienia zbioru $M$, albo $\lim\limits_{a \to x}~f(a) = f(x).$

Należy także zwracać bacznie uwagę na kolejność kwantyfikatorów we wzorze na ciągłość w sensie Cauchy'ego dla danego zbioru. Przesunięcie pierwszego kwantyfikatora na trzecią pozycję, mianowicie

$\forall_{\varepsilon > 0}\; \exists_{\delta > 0}\; \forall_{x \in M}\; \forall_{y \in M}\; |x-y| < \delta \implies |f(x) - f(y)| < \varepsilon$,

prowadzi do sformułowania o wiele silniejszej własności, tzw. ciągłości jednostajnej.

Obie definicje (Cauchy'ego i Heinego) są równoważne już przy założeniu bardzo słabej wersji aksjomatu wyboru, i nie jest on potrzebny dla dowodu równoważności globalnej ciągłości w odpowiednich znaczeniach.

Ciągłość jednostronna

Rozpatruje się czasami funkcje ciągłe jednostronnie: lewo- i prawostronne. Dla definicji Cauchy'ego należy dodać warunek dla $y$, mianowicie $y < x$, aby otrzymać funkcję ciągłą lewostronnie. Definicja funkcji ciągłej prawostronnie wymaga zmiany powyższej nierówności na przeciwną. Definicja Heinego wymaga wybrania dowolnego ciągu zbliżającego się do $x$ wyłącznie punktami z lewej lub prawej strony.

Przykłady

Rozpatrujemy funkcje $\cdot\colon \mathbb R \to \mathbb R$.

• Wszystkie funkcje elementarne są ciągłe w swojej dziedzinie (co jest również prawdą dla funkcji $\cdot\colon \mathbb C \to \mathbb C$).
• Funkcja dana wzorem

$f(x) = \begin{cases} \tfrac{\sin x}{x} & \mbox{dla } x \ne 0 \\\; 1 & \mbox{dla } x = 0 \end{cases}$

jest ciągła.

• Funkcja Dirichleta $D$ jest nigdzie ciągła (tzn. nie jest ciągła w żadnym punkcie swojej dziedziny).
  • Funkcja $D_1(x) = x \cdot D(x)$ jest ciągła wyłącznie w punkcie $x = 0$.
  • Funkcja $D_{\mathbb Z} = \sin(x \pi) \cdot D(x)$ jest ciągła we wszystkich całkowitych punktach dziedziny.
• Funkcja Riemanna $R$ jest ciągła we wszystkich niewymiernych i nieciągła we wszystkich wymiernych punktach dziedziny.

Przestrzenie metryczne i unormowane

W przestrzeniach metrycznych i przestrzeniach unormowanych stosuje się nieznacznie tylko zmodyfikowane wersje definicji Cauchy'ego zastępując każdą wartość bezwzględną różnicy odpowiednią dla każdej przestrzeni metryką lub normą różnicy.

Dla przestrzeni metrycznych $(X, d_X)$ oraz $(Y, d_Y)$ funkcja $f\colon X \to Y$ jest ciągła, jeśli prawdziwy jest wzór

$\forall_{x \in X}\; \forall_{\varepsilon > 0}\; \exists_{\delta > 0}\; \forall_{y \in X}\; d_X(x, y) < \delta \implies d_Y(f(x), f(y)) < \varepsilon$.

Powyższą implikację można zapisać również w postaci

$f(B_X(x, \delta)) \subseteq B_Y(f(x), \varepsilon)$

albo

$B_X(x, \delta) \subseteq f^{-1}\big(B_Y(f(x), \varepsilon)\big)$,

gdzie $B_X,\ B_Y$ są kulami odpowiednio w $X,\ Y$, a w nawiasach po oznaczeniu kuli pisze się jej środek i promień.

Przestrzenie topologiczne

Ciągłość funkcji w punkcie: dla otoczenia $V$ punktu $f(x)$ możemy znaleźć otoczenie $U$ punktu $x$ takie, że $f(U)$ jest zawarte w $V$ (czyli $U$ jest zawarte w przeciwobrazie $V$)

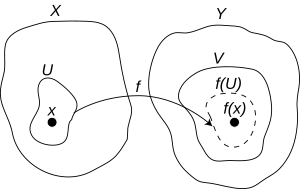
Najpełniejszą oraz najogólniejszą definicję ciągłości wprowadza się w topologii.

Niech $(X, \tau_X)$ oraz $(Y, \tau_Y)$ będą przestrzeniami topologicznymi, a $f\colon X \to Y$ przekształceniem między nimi. Powiemy, że $f$ jest ciągłe, jeśli przeciwobraz dowolnego zbioru otwartego w $Y$ jest zbiorem otwartym w $X$, co zapisuje się następująco:

$\forall_{U \in \tau_Y}\; f^{-1}(U) \in \tau_X$.

Równoważnie można wymagać, aby przeciwobraz zbioru domkniętego był domknięty. Jeśli przestrzenie $X,\ Y$ są metryzowalne, to powyższa definicja zgadza się z definicją ciągłości w sensie Cauchy'ego podaną wyżej.

Własności

• Złożenie funkcji ciągłych jest funkcją ciągłą.

Funkcja rzeczywista, której dziedziną jest przedział domknięty

Jeśli funkcja $f\colon [a, b] \to \mathbb R$ jest ciągła, to $f$ na swojej dziedzinie

• jest jednostajnie ciągła,
• przyjmuje swoje ekstrema (zob. twierdzenie Weierstrassa),
• ma własność Darboux (zob. twierdzenie Darboux).

Topologia

Niech $(X, \tau_X)$ i $(Y, \tau_Y)$ będą przestrzeniami topologicznymi oraz $f, g\colon X \to Y$.

Aby sprawdzić ciągłość funkcji $f$, nie trzeba badać wszystkich elementów topologii danej przestrzeni, lecz wystarczy to zrobić dla pewnej jej bazy $\mathcal B$:

$\forall_{U \in \mathcal B}\; f^{-1}(U)\in \tau_X$.

Ciągłość można także badać za pomocą zbiorów domkniętych. Mianowicie, funkcja $f$ jest ciągła, jeżeli zachodzi jakikolwiek z następujących warunków:

• przeciwobraz dowolnego zbioru domkniętego w $Y$ jest domknięty w $X$;
• dla każdego zbioru $A \subseteq X$ mamy $f(\operatorname{cl}\;A) \subseteq \operatorname{cl}\;f(A)$, gdzie $\operatorname{cl}$ jest operatorem domknięcia;
• dla każdego zbioru $B\subseteq Y$ zachodzi $\operatorname{cl}\;f^{-1}(B) \subseteq f^{-1}(\operatorname{cl}\;B)$.

Przy przekształceniach ciągłych zachowywane są takie własności przestrzeni jak:

• zwartość,
• ośrodkowość,
• spójność.

Jeśli zbiór $D$ jest gęsty w $X$, $f$ i $g$ są ciągłe, oraz $f\bigg|_D = g\bigg|_D$, to $f = g$.

Niech $I \subseteq \mathbb N$ oraz $X = \prod_{i \in I}~X_i$ będzie produktem Tichonowa, wówczas dla $j \in I$ przekształcenie

$\pi_j\colon\ X\ni x = \langle x_i\colon i \in I \rangle \mapsto x_j\in X_j$

jest ciągłym rzutem na $j$-tą współrzędną.

Przestrzeń funkcji ciągłych

W topologii i analizie funkcjonalnej często bada się przestrzeń, której elementami są funkcje ciągłe z pewnej przestrzeni topologicznej $X$ w inną $Y$. Taka przestrzeń jest oznaczana symbolem $\mathcal C(X, Y)$ i jest szczególnym przypadkiem przestrzeni funkcyjnej.

Jednym z najbardziej popularnych przykładów są przestrzenie funkcji ciągłych o wartościach w liczbach rzeczywistych. Pierścień $\mathcal C(X, \mathbb R)$ o elementach będących odwzorowaniami ciągłymi z $X$ w $\mathbb R$ i operacjach algebraicznych wprowadzanych „punktowo” jest ważnym obiektem topologicznym. Przeprowadzono wiele badań w poszukiwaniu związków struktury algebraicznej tego pierścienia ze strukturą topologiczną przestrzeni $(X, \tau_X)$.

Na przestrzeni $\mathcal C(X, \mathbb R)$ rozważa się także strukturę topologiczną wprowadzając topologie:

zbieżności punktowej, 

zgodną z topologią Tichonowa na iloczynie $\prod_{x \in X}~\mathbb R;$

zbieżności jednostajnej, 

w której bazą otoczeń punktu $f \in \mathcal C(X)$ jest $\{U_n(f)\colon\ n = 1, 2, 3, \dots\}$, gdzie $U_n(f) = \left\{g \in \mathcal C(X)\colon\ \forall_{x \in X}\; |f(x) - g(x)| < \tfrac{1}{n}\right\}$.

Pojęcie teorio-mnogościowe

Niech $(A, \le_A)$ oraz $(B, \le_B)$ będą porządkami zupełnymi, wtedy funkcja $f: A \to B$ jest ciągła, jeżeli zachowuje kresy górne podzbiorów skierowanych, tzn:

Niech $X \subseteq A$ będzie podzbiorem skierowanym, wtedy $f(\sup X) = \sup f(X).$

Zobacz też

• warunek Lipschitza
• warunek Höldera
• funkcja różniczkowalna
• punkt odosobniony
• funkcja jednostajnie ciągła