Spektroskopia astronomiczna
Spektroskopia astronomiczna, astrospektroskopia[1] – dział astrofizyki, który używa metod spektroskopii do badania ciał niebieskich. Spektroskopia astronomiczna jest obecnie głównym narzędziem badawczym astronomii.
Fotometria astronomiczna to badanie natężenia, czyli jasności promieniowania określonej długości fali elektromagnetycznej, zaś spektroskopia bada rozmieszczenie i szerokość linii widmowych. Na podstawie widma wnioskuje się o właściwościach ośrodka, w którym powstała fala, lub przez który została pochłonięta. Porównując wyniki badań widm ciał niebieskich z liniami uzyskiwanymi dla pierwiastków i związków chemicznych w laboratorium można wnioskować np. o składzie chemicznym gwiazd. Rozkład widmowy światła zależy także od temperatury, opisuje to model ciała doskonale czarnego. Dzięki temu można wyznaczyć temperaturę powierzchniową gwiazd. Badając przesunięcie charakterystycznych linii w widmie zgodnie z efektem Dopplera, uzyskuje się informacje o prędkości przybliżania albo oddalania się gwiazdy. W opisie układów podwójnych i wielokrotnych można na podstawie wielkości amplitud zmian prędkości gwiazd układu wnioskować o ich masie.
Historia spektroskopii astronomicznej[edytuj | edytuj kod]
| Oznaczenie Fraunhofera |
Długość fali (nm) |
Chemiczne pochodzenie linii |
Szerokość równoważna (pm) |
|---|---|---|---|
| A | 759,370 | atmosferyczny O2 | – |
| B | 686,719 | atmosferyczny O2 | – |
| C | 656,281 | wodór alfa (Hα) | 402,0 |
| D1 | 589,592 | obojętny sód (Na I) | 56,4 |
| D2 | 588,995 | obojętny sód (Na I) | 75,2 |
| E | 527,039 | obojętne żelazo (Fe I) | |
| F | 486,134 | wodór beta (Hβ) | 368,0 |
| G | 431,42 | CH molekuła | |
| H | 396,847 | zjonizowany wapń (Ca II) | 1546,7 |
| K | 393,368 | zjonizowany wapń (Ca II) | 2025,3 |
| L | 382,044 | żelazo | |
| N | 358,121 | żelazo | |
| P | 336,112 | zjonizowany tytan | |
| T | 302,108 | żelazo |
Początków spektroskopii jako gałęzi naukowej można szukać w badaniach Newtona, który w 1666 roku rozszczepił światło przy pomocy pryzmatu i uzyskał obraz widmowy światła słonecznego. O swoim odkryciu i obserwacjach napisał w książce z 1704 r. pt. Optics, gdzie wyjaśnia naturę koloru, oraz zależność od niego współczynnika załamania światła. Na początku XVIII w. także inni uczeni (Kartezjusz, R. Hooke, W. Herschel) przeprowadzili ten eksperyment. Dla lepszego przestudiowania zjawiska W. Wollaston zastosował w swoim eksperymencie zamiast pryzmatu szczelinę i jako pierwszy odkrył linie absorpcyjne Słońca, zaobserwował 7 ciemnych linii, wśród nich dublet sodowy, nie przypisał jednak im żadnego znaczenia. Uczynił to natomiast niemiecki optyk, Joseph von Fraunhofer, który – dołączając do lunety dyspersyjny element optyczny – znalazł w widmie słonecznym około 600 takich linii (dziś nazywanych od jego nazwiska liniami Fraunhofera); wyznaczył dokładną pozycję 350 z nich, obliczając współczynnik załamania światła o odpowiadającej ich pozycji barwie. W ten sposób w 1814 roku narodziła się spektroskopia astronomiczna.
Współcześnie z odkryciem Fraunhofera, w 1823, William Fox Talbot i John Herschel badali związek między składem spalanej substancji a kolorem płomienia, wykazując, że na tej podstawie można przeprowadzić analizę chemiczną. Sir David Brewster w 1832 r. odkrył, że linie Fraunhofera można wytworzyć także w warunkach ziemskich. W widmie światła słonecznego przepuszczonego przez opary kwasu azotowego, naliczył ok. 2000 linii. Zaobserwował także, iż liczba linii rośnie, gdy zwiększa się grubość warstwy gazu, jej gęstość lub temperatura. Na podstawie tego doświadczenia Brewster wnioskował, że atmosfera ziemska absorbuje światło o pewnych kolorach z białego światła słonecznego – w ich miejscu obserwujemy linie Fraunhofera. W 1849 roku Foucault badając widma rozmaitego pochodzenia doszedł do zasadniczego przekonania: absorpcyjna lub emisyjna postać spektrum zależy od tego, czy światło dociera do obserwatora bezpośrednio ze źródła, czy opuszczając źródło przechodzi przez jakąś materię.



W 1859 r. Kirchhoff, wykorzystując wyniki Foucaulta i Bunsena ustanowił 3 podstawowe prawa klasycznej analizy spektralnej:
- Rozgrzane do wysokiej temperatury ciała stałe, ciecze, a także gazy pod wysokim ciśnieniem emitują promieniowanie o ciągłym, pozbawionym linii widmowych spektrum, zwanym kontinuum.
- W widmie gazów w wysokiej temperaturze i przy niewielkim ciśnieniu, ukazują się oddzielne linie. Każda z nich należy do konkretnej serii linii widmowych konkretnego pierwiastka; widmo świecącego gazu zdradza jego skład chemiczny.
- Gdy światło o widmie ciągłym przebiega przez chłodniejszy gaz, wtedy na tle kontinuum obserwujemy ciemne linie w miejscach, gdzie obserwowalibyśmy linie emisyjne, gdyby to ten gaz świecił. Mówiąc inaczej: promieniowanie pochłaniane przez określony pierwiastek chemiczny ma takie same długości fali, jakie miałoby promieniowanie przez niego emitowane.
Podstawy teoretyczne spektroskopii[edytuj | edytuj kod]
Spektroskopia atomów – wstęp[edytuj | edytuj kod]
Już w XIX wieku naukowcy zauważyli, że linie widmowe pierwiastków układają się w charakterystyczne ciągi. W 1888 r. Johannes Rydberg ogłosił wzór, opisujący wszystkie linie atomu wodoru. Brak było jednak jego teoretycznego uzasadnienia. Pierwszą teorią wyjaśniającą prawidłowości w widmie atomu wodoru był model atomu Bohra. Według niego, widmo liniowe powstaje w wyniku przeskoku elektronu między dozwolonymi poziomami energetycznymi w atomie. Przeskoki na dany poziom energetyczny z wyższych tworzą serie linii, które zagęszczają się w kierunku końca linii, odpowiadającego przeskokom z coraz wyższych poziomów, oraz wychwyconych swobodnych elektronów. W każdym przypadku długość fali powstającego promieniowania jest odwrotnie proporcjonalna do różnicy energii elektronu swobodnego oraz poziomu energetycznego osiągniętego przez elektron na orbicie (na podstawie III prawa Bohra). W związku z tym, że początkowe energie wolnych elektronów znacznie się od siebie różnią, przy przyjmowaniu elektronów powstają fale o różnej długości, które „rozmazują się” po widmie.
Spektrum atomu wodoru i jonów wodoropodobnych[edytuj | edytuj kod]
Częstotliwość fali świetlnej emitowanej przez atom odpowiada zmianie energii atomu zgodnie ze wzorem ν = E/h. Gdy elektron atomu wodoru zmienia swój stan energetyczny przechodząc na inny, o mniejszej głównej liczbie kwantowej, wtedy nadwyżka energii zostaje wypromieniowana jako kwant światła. Na widmo atomu wodoru składają się m.in. następujące serie:

Seria Lymana znajduje się w ultrafiolecie, seria Balmera ma 4 linie w świetle widzialnym, natomiast pozostałe serie leżą w podczerwieni. Linie serii opisuje jeden wzór zwany regułą Rydberga. Spektra jonów zawierających jeden elektron, czyli jednokrotnie zjonizowanego helu (He+), dwukrotnie zjonizowanego litu (Li2+), trzykrotnie zjonizowanego berylu (Be3+) itp. ukazują silne podobieństwo do spektrum atomu wodoru. Według modelu Bohra możliwe poziomy energetyczne takich jonów są podobne do poziomów atomu wodoru, mnożonego przez kwadrat liczby atomowej pierwiastka (Z), dlatego różnice energii atomu i odpowiadające im promieniowanie, mogą być wyrażone wzorem:
Wśród serii wyemitowanych przez zjonizowany hel (jon He+, Z=2) w widmie gwiazdy ζ gwiazdozbioru Rufy jeszcze w 1897 r. odkryto serię Pickeringa:
którą na początku uważano za serię widma atomu wodoru. Na podstawie modelu atomu Bohra znaleziono powyższe serie w liniach widmowych He+, obserwując światło wytworzone przez wyładowania elektryczne w helu.
Widmo jednoelektronowego atomu wodoru jest najprostsze ze znanych. Im cięższy atom tym więcej ma elektronów i wskutek tego bardziej skomplikowane widmo.
Widmo atomowe metali alkalicznych[edytuj | edytuj kod]

Pierwiastki alkaliczne znajdują się w I grupie głównej układu okresowego, na ich powłoce walencyjnej znajduje się jeden elektron, dlatego pierwiastki te pod względem swoich właściwości najbardziej przypominają wodór, w którego atomie jest tylko 1 elektron. Najbardziej zewnętrzny elektron nazywany jest w spektroskopii elektronem świecącym, a w chemii elektronem walencyjnym (elektronem wartościowości). Pierwsza z nazw związana jest z tym, że widmo optyczne metali alkalicznych powstaje na skutek wzbudzenia tego elektronu, pozostałe natomiast wyrażają rolę elektronu we właściwościach chemicznych pierwiastków. Elektron ten w atomie pierwiastka alkalicznego może być traktowany jak w atomie wodoru przyjmując, że wewnętrzne elektrony zmniejszają ładunek wytwarzający centralne pole elektryczne, tworząc tzw. zrąb atomowy. Prawdopodobieństwo przebywania elektronu walencyjnego w zrębie zależy od pobocznej liczby kwantowej, dlatego jego energia – w przeciwieństwie do energii atomu wodoru – oprócz głównej liczby kwantowej, zależy także od liczby pobocznej.
Energia stanu gdzie Energia stanu gdzie
to prędkość światła, =6,626·10−34 Js (stała Plancka), =1,097·107 m−1 (stała Rydberga), oraz – człony korekcyjne tym większe, im cięższy jest atom (dla atomu wodoru ich wartość wynosi 0) i im mniejsza jest wartość pobocznej liczby kwantowej. (Podobnie jak przy atomie wodoru poboczna liczba kwantowa musi być mniejsza niż główna liczba kwantowa.) Widmo optyczne powstaje w ten sposób, że różnica pomiędzy dwoma poziomami energetycznymi zostaje wypromieniowana w postaci kwantu światła. Podczas badania widma emisyjnego można zauważyć 4 bardziej intensywne, po części zachodzące na siebie ciągi linii: ciąg główny, pierwszy i drugi ciąg poboczny oraz ciąg Bergmanna. Ciągi, z wyjątkiem ciągu głównego, prowadzące do wspólnego poziomu tworzą serie zbieżne do wspólnej granicy. W tym przypadku ciąg poboczny I i II.
Ciąg główny: gdzie II ciąg poboczny: gdzie I ciąg poboczny: gdzie Ciąg Bergmanna: gdzie
Widmo absorpcyjne powstaje, gdy gaz alkaliczny nie ma bardzo wysokiej temperatury, wówczas jego atomy są w stanie podstawowym i obserwujemy wyłącznie ciąg główny. Z granicą każdego ciągu łączy się widmo ciągłe, podobnie jak w wypadku widma atomu wodoru.
Spektroskopia cząsteczek[edytuj | edytuj kod]
Zasadniczo można wyróżnić dwa typy widma: ciągłe oraz nieciągłe. Widma nieciągłe mogą składać się z linii lub pasm, zależnie od tego, czy widmo wytwarzane jest przez atom czy cząsteczkę. Widma liniowe dzielą się na seryjne i multipletowe. W widmach seryjnych do poziomu podstawowego dołącza nieskończony ciąg wyższych poziomów energetycznych. Widmo takie obserwuje się dla atomów z jednym elektronem walencyjnym, np. dla wodoru. Widma multipletowe posiadają atomy o większej liczbę elektronów walencyjnych, w których możliwe jest więcej różnych przeskoków między poziomami. W miejsce linii pojawiają się grupy linii, czyli multiplety. W widmach cząsteczek obserwuje się zarówno widmo liniowe, jak i pasmowe. Pasma są układem wielu linii położonych blisko siebie w pewnym zakresie widma, które można przy dostatecznej precyzji sprzętu badawczego rozdzielić na nieznacznie różniące się energią podpoziomy.
Istnienie pasm oznacza, że cząstki emitujące promieniowanie nie mają ściśle określonych poziomów energetycznych, lecz mogą przyjmować je w pewnym zakresie.
Linie widmowe cząsteczki tworzą się w znacznie bardziej skomplikowany sposób niż linie widmowe atomów. Wkład do widma dają obroty cząsteczki jako całości, a także drgania rdzeni atomów tworzących cząsteczkę. Dlatego, w przybliżeniu – zaniedbując wzajemny wpływ na siebie tych trzech ruchów – całkowita energia cząsteczki to suma energii elektronów, drgań wewnątrzcząsteczkowych oraz energii obrotowej. Energia drgań i wirowania cząsteczki jest skwantowana, podobnie jak energia elektronu w atomie. Gdy cząsteczka znajdująca się w stanie wzbudzonym przechodzi na niższy poziom energetyczny, wypromieniowuje różnicę energii w postaci fotonu; zmiana energii może być wywołana jednym lub kilkoma rodzajami przejść np. jednoczesną zmianą energii drgań cząstki i energii elektronu w cząstce.
Na tej podstawie linie widma cząsteczek możemy podzielić na 3 typy:
- czysto rotacyjne, gdy zmienia się tylko energia obrotowa, natomiast stan elektronów oraz drgań pozostaje bez zmian; energie te są niewielkie, dlatego pasma odpowiadające tym przejściom znajdują się w zakresie mikrofal oraz podczerwieni,
- wibracyjno-rotacyjne, gdy zmienia się stan drgań i obrotów, a nie zmienia się stan elektronów – przejściom tym odpowiada średnia energia i pasma te znajdują w bliskiej podczerwieni,
- z pasmami elektronowymi, w których wypadku zmieniają się wszystkie trzy stany – tak powstałe pasma znajdują się w podczerwieni, świetle widzialnym oraz w ultrafiolecie.
Badanie widm ostatniego typu jest bardzo ważne, gdyż z ich pomocą można ustalić odległości jąder w cząsteczce, częstotliwość drgań rdzenia, czy też rozkład elektronów. Stany poszczególnego elektronu można scharakteryzować przy pomocy liczb kwantowych oraz właściwości symetrii. Przez analogię do oznaczeń stanów w atomach (s, p, d, f,..), w molekułach dwuatomowych wprowadza się stany cząsteczek (Σ, Π, Δ, Φ,...) w ten sposób, że rzut całości momentu orbitalnego elektronu na oś cząsteczki to 0, 1, 2,...-krotność stałej Diraca.
W przypadku spektroskopii astronomicznej w pewnych przypadkach mogą pojawić się linie odpowiadające tzw. przejściom zabronionym. Są to takie linie widmowe, które nie powstają w warunkach laboratoryjnych, ponieważ do ich wystąpienia potrzebne są ekstremalne warunki fizyczne (np. wyjątkowo niska gęstość). Takimi „zabronionymi” liniami są linie widmowe jedno- i dwukrotnie zjonizowanego tlenu (O+, O2+), trzy- i czterokrotnie zjonizowanego neonu (Ne3+, Ne4+), jedno- i dwukrotnie zjonizowanej siarki (S+, S2+), trzy- i czterokrotnie zjonizowanego argonu (Ar3+, Ar4+). Warunki potrzebne do powstania takich linii są spełnione w mgławicach emisyjnych. Te obiekty mają zwykle 10–100 parseków średnicy, a ich gęstość dochodzi do 10 tysięcy atomów/cm³, co jest niezwykle niską wartością.
Absorpcja i emisja promieniowania[edytuj | edytuj kod]
Poziomy energetyczne w modelu Bohra są stanami stacjonarnymi; przejście z jednego stanu w inny może się odbyć się tylko w wyniku oddziaływania z inną cząstką (np. fotonem). Procesy wywołane oddziaływaniem cząstki na atom mogą być zasadniczo dwóch typów: wzbudzenie lub jonizacja. Elektron o dużej energii kinetycznej może oddać jej część, przeprowadzając mijany atom do stanu wzbudzonego. Możliwe są następujące reakcje:
- A + eszybki → A* + ewolny (1) A* → A + hν (2) A + hν → A* (3)
gdzie A* oznacza atom wzbudzony, e – elektron. Wzbudzony atom dąży do jak najszybszego przejścia w niższy stan energetyczny, co osiąga w procesie (2). Przez hν oznaczony jest tutaj kwant światła. Każdy proces wymiany energii między atomem a cząstkami jest odwracalny, atom może być wzbudzony światłem (3).
W trakcie jonizacji atom otrzymuje energię od wysokoenergetycznego elektronu (4) lub fotonu (5), a jeden z elektronów w atomie osiąga energię wyższą niż najwyższa możliwa energia wzbudzenia i opuszcza atom. Tę reakcję zapisuje się następująco:
- A + eszybki → A+ + e + ewolny (4) A + hνv → A+ + e + Ekin, (5)
gdzie A+ oznacza jednokrotnie zjonizowany atom. Jonizacja może się odbywać także poprzez przyjmowanie fotonów, mówimy wtedy o fotojonizacji. Może ona zajść tylko wtedy, gdy foton ma energię wyższą niż najwyższa możliwa energia wzbudzenia w danym atomie. Proces odwrotny, czyli przyjęcie elektronu przez atom, nazywa się rekombinacją. Elektron może od razu przejść do stanu o najniższej energii (6), lub zająć któryś z poziomów wzbudzonych, a z niego przejść do stanu podstawowego (7):
- A+ + e + Ekin → A + hv (6) A+ + e + Ekin → A* + hv1 → A + hv1 + hv2 (7)
Linie widmowe powstają także podczas tzw. perturbacji. Wolny elektron przelatując w sąsiedztwie atomu doznaje przyspieszenia i – jak naładowana, przyspieszająca cząstka – wytwarza promieniowanie elektromagnetyczne. Ponieważ stany podstawowe wolnego elektronu nie są skwantowane, powstające widmo emisyjne jest ciągłe.
Profile linii, poszerzenie linii, szerokość równoważna[edytuj | edytuj kod]

Linie widmowe nie są nieskończenie cienkie, natężenie promieniowania maleje lub rośnie (w zależności od tego, czy linia jest absorpcyjna na czy emisyjna) w sposób ciągły od poziomu kontinuum w stronę środka linii z obydwu kierunków. Przy analizie absorpcyjnych linii widmowych ważnymi jej parametrami jest jej intensywność oraz szerokość.
Szerokość równoważna Linie absorpcyjne mogą być wąskie a intensywne, jak i szerokie, ale o mniejszej intensywności. W celu porównywania intensywności linii Minnaert i współpracownicy wprowadzili termin szerokość równoważna linii spektralnej. Szerokość równoważna odpowiada takiej linii w obszarze której następuje całkowite pochłanianie i mającej kształt prostokąta, którą miałaby takie samo pole jak rzeczywista linia, co odpowiada wyrażeniu:
gdzie: to irradiancja spektralna kontinuum, irradiancja spektralna linii widmowej.
Szerokość równoważna nie jest parametrem określającym szerokość linii a jej intensywność. O zależności szerokości równoważnej poszczególnych linii widmowych od parametrów fizycznych gazu pochłaniającego promieniowanie można wnioskować na podstawie modelu Schustera-Schwarzschilda.
Profil linii widmowej powstaje, gdyż w zakresie częstotliwości linii widmowej wzrasta współczynnik absorpcji ponieważ w tym interwale częstotliwości atom jest zdolny zaabsorbować spektrum elektromagnetyczne. Aby móc wyznaczyć profil linii w sposób teoretyczny, trzeba znać zależność od częstotliwości. Współczynnik absorpcji składa się z dwóch składowych: współczynnika absorpcji ciągłej, oraz współczynnika absorpcji selektywnej. Poza linią widmową uwzględnia się tylko natomiast w zakresie częstotliwości linii widmowej sumę
- – częstotliwość widma
- – natężenie widma kontinuum w okolicy częstotliwości
- – natężenie widma dla częstotliwości w obszarze linii widmowej.
Profil linii
Tworząc wykres zależności natężenia od długości fali, otrzymujemy profil (kontur) linii. Odcinek środkowy to centrum linii, dwie zewnętrzne części nazywamy skrzydłami, wszystkie trzy części razem dają szerokość linii. W praktyce sąsiednie linie często się stapiają („blend”), wtedy trudno jest zmierzyć szerokość linii. Wielkość nazywamy natężeniem resztkowym. Poza obszarem częstotliwości linii widmowej wewnątrz linii absorpcyjnej

Profil linii absorpcyjnych, głównie jej szerokość, jest inna przy prowadzeniu doświadczeń na Ziemi, jak i dla światła docierającego z kosmosu. Najprostszym parametrem określającym szerokość linii jest jej szerokość połówkowa, choć częściej mówi się o profilu linii widmowych. Profil linii powstających w fotosferze gwiazd tworzony jest przez widmo ciągłe oraz absorpcję selektywną.
Wyróżnić można dwa rodzaje absorpcji selektywnej. Zależnie od przypadku występuje tylko jeden rodzaj absorpcji (np. czyste rozproszenie). O rzeczywistej absorpcji selektywnej mówimy, gdy foton jest zaabsorbowany przez atom, którego wzbudza. Wzbudzony elektron w czasie ok. 10·10−12s schodzi na niższy poziom energetyczny. Jednakże w przypadku rzeczywistej absorpcji nie zawsze wraca do stanu wyjściowego, wówczas energia pochłoniętego fotonu nie jest równa energii fotonu wyemitowanego wskutek przejścia elektronu w niższy stan energetyczny. Czyste rozproszenie ma miejsce wtedy, gdy po zaabsorbowaniu fotonu o częstotliwości następuje emisja fotonu o tej samej częstotliwości Emitowany foton ma inny kierunek niż foton pochłonięty w wielu przypadkach fotony rozproszone są równomiernie rozłożone we wszystkich kierunkach, dlatego w wyniku rozproszenia z wiązki równoległych promieni powstaje wiązka izotropowa, a w wiązce przechodzącej brak jest fal które zostały pochłonięte.
Badanie profilu linii, w tym i jej parametru poszerzenia linii widmowej, danej gwiazdy (źródła światła) jest ważne, gdyż z nich można wnioskować o wielu właściwościach fizycznych tego ciała niebieskiego. Są to:
- warunki fizyczne gazu tworzącego atmosferę gwiazd,
- szybkość obrotowa,
- ewentualna pulsacja,
- wiatr gwiezdny,
- utrata masy,
- plamy powierzchniowe (plamy słoneczne),
- materia otaczająca gwiazdę,
- ewentualna podwójność.
Poszerzenie linii widmowych
W trakcie badań zaobserwowano, że linie spektralne nie składają się z nieskończenie cienkich linii, ale następuje ich rozciąganie, zależne od długości fali. To zjawisko można tłumaczyć korzystając z zasady nieoznaczoności Heisenberga, wedle której nie można wyznaczyć wartości dwóch nie zamiennych na siebie wielkości fizycznych w jednakowym czasie i z dowolną dokładnością. Na przykład energia stanu kwantowego oraz czas jego trwania podlegają następującej zależności: gdzie czas trwania stanu wzbudzonego, stała Plancka, natomiast oznacza niepewność energii stanu kwantowego.
Inny powód poszerzenia linii to poszerzenie pod wpływem oddziaływań – w wyniku zderzeń atomowych skraca się czas utrzymywania stanu wzbudzonego, przez co atomy szybciej przechodzą do stanu podstawowego, zwiększając nieokreśloność energii. Trzeci powód to poszerzenie termiczne wywołane efektem dopplerowskim spowodowanym ruchami termicznymi atomów. Poszerzenie to jest zwykle większe o 1–2 rzędy wielkości od naturalnego poszerzenia. Poza procesami mikroświata dalsze poszerzanie linii może być spowodowane rotacją lub pulsacją gwiazd.
Na pomiar dopplerowskiego poszerzenia linii bezpośrednio wpływa rozdzielczość (nm/pixel; angstrem/pixel) spektrografu. Gdy mierzymy w tych samych jednostkach, wzór Dopplera można zapisać następująco: gdzie długość fali centrum zaobserwowanego obszaru, miara rozdzielczości spektrografu, prędkość światła i prędkości radialnej czynnika pochłaniającego lub emitującego promieniowanie.
Promieniowanie termiczne[edytuj | edytuj kod]

Dla większości gwiazd rozkład energii widma w pewnym, czasem dość szerokich, obszarów widma odpowiada rozkładowi obserwowanemu dla widma ciała doskonale czarnego. Rozkład opisuje wzór Plancka, który wyrażony dla długości fali:
gdzie to stała Plancka (h=6,54·10−27 erg/s) stała Boltzmanna (k=1,36·10−16 erg/grad) prędkość światła, temperatura absolutna ciała. Z rozkładu prawa Plancka wynikają dwa prawa stosowane często w astronomii – to prawo Stefana-Boltzmanna oraz prawo Wiena. Prawo Stefana-Boltzmanna mówi, że całkowita energia wypromieniowana przez jednostkę powierzchni ciała doskonale czarnego o temperaturze T w jednostce czasu jest proporcjonalna do czwartej potęgi jego temperatury:
W myśl prawa Wiena iloczyn długości fali odpowiadającej maksimum krzywej Plancka oraz temperatury T jest stały.
Teoria linii widmowych typu Fowler-Milne[edytuj | edytuj kod]
Elektrony otoczki elektronowej atomu mogą przyjmować tylko dokładnie określone (stacjonarne) poziomy energetyczne. Poziom energetyczny -krotnie zjonizowanego atomu: energia tego poziomu: Atom może zaabsorbować jedynie promieniowanie o częstotliwości, dla której spełnione jest równanie: gdzie spełniona jest nierówność
Natężenie oraz profil linii widmowej odpowiadającej przejściu zależy od tego, jak wiele atomów danego typu znajduje się w fotosferze gwiazdy oraz czy w znaczącej ilości pojawia się -krotnie zjonizowany stan. W identycznych warunkach natężenie linii spektralnej zależne jest od proporcji jonizacji w atmosferze gwiazdy, czy też od temperatury.
Teoria Fowler-Milne z pomocą równania Saha bada, w jaki sposób liczba elektronów na określonym poziomie oraz przybliżone natężenie linii widmowej zależne są od temperatury. Obowiązujące w przypadku równowagi termodynamicznej równanie Sahy podaje relatywną liczbę atomów o różnych stanach jonizacyjnych:
gdzie to -krotnie zjonizowanych atomów będących na -tym stanie wzbudzenia, statyczny ciężar pojedynczego stanu (można uzyskać z tablic), gęstość elektronowa, energia jonizacji, masa elektronu. Badając linie widmowe atomów o różnym stopniu zjonizowania w widmie gwiazd, np. z pomocą krzywej rosnącej, można ustalić proporcję z czym można określić z równania temperaturę jonizacji gwiazdy. W stanie równowagi termodynamicznej wypełnia się równanie Boltzmanna, na podstawie którego można ustalić TG, tzw. temperaturę wzbudzenia:
gdzie spośród -razy jonizowanych atomów danych pierwiastków chemicznych, ich pierwszy numer objętościowy, które znajdują się w -razowym stanie kwantowym, energia wzniecania takiego samego gatunku -razowo jonizowanego -stanowego atomu. W widmie gwiazdy równoważna szerokość tych linii spektralnych, a u których przejście elektronu dzieje się ze stanu jest proporcjonalne z Z dwóch różnych serii widmowych tego samego atomu stwierdzić można stosunek
Efekt Zeemana[edytuj | edytuj kod]

Pieter Zeeman (1865–1943) holenderski fizyk w 1896 odkrył, że gdy substancja emitująca światło znajduje się w polu magnetycznym, to powstające linie spektralne rozszczepiają się na kilka linii. Komponent pozostaje na miejscu natomiast dwa komponenty przesuwają się symetrycznie w stronę fal dłuższych i krótszych. Wyjaśnieniem zjawiska jest fakt rozdziału stanu energetycznego elektronu znajdującego się w polu magnetycznym w zależności od momentu magnetycznego elektronu. Podział możliwego stanu energetycznego w polu magnetycznym obserwujemy jako rozdzielenie linii widmowej.
Rozróżnia się dwa rodzaje efektu Zeemana: normalny i anormalny. Efektem normalnym nazywa się rozszczepienie wynikające z orbitalnego momentu pędu elektronu (S=0, L≠0), zjawisko to wytłumaczono przy użyciu mechaniki klasycznej po odkryciu efektu. Różnica energii jest równa energii dipola magnetycznego, jakim jest ruch ładunku elektronu wokół jądra atomowego, zewnętrznym w polu magnetycznym. Energię tę określa wzór: ΔW=mJ μB B, gdzie jest indukcją pola magnetycznego, a μB jest momentem magnetycznym, a odpowiadająca tej energii różnica częstotliwości to zatem: Δν = ΔW/h ≈ 14 GHz/T. Komponenty linii widmowych wodoru w polu magnetycznym o indukcji 1 tesli będą się różniły o Δv = 1,4·1010 Hz. Oznacza to bardzo małą rozpiętość w widmie (3% odległości komponentów linii atomu sodu w analogicznej sytuacji). Aby ją zaobserwować należy dysponować spektrometrem o zdolności rozdzielczej ≥ 106.
W przypadku anormalnego efektu Zeemana w atomie zarówno jak i Z tego powodu pojawia się więcej linii widmowych, niż dla efektu normalnego. Wtedy efekt Zeemana wywołuje także polaryzacji komponentów linii widmowej. Jej sposób i wartość zależą od kąta wyznaczonego przez wektor natężenia pola magnetycznego i kierunek obserwacji. Rozbicie łatwiej badać w wypadku linii emisyjnych. Gdy umieścimy w polu magnetycznym gaz emitujący światło, a kierunek pola magnetycznego pokrywa się z kierunkiem obserwacji, wtedy przy normalnym efekcie Zeemana zaobserwujemy tylko dwa oddalone komponenty których światło będzie spolaryzowane liniowo prostopadle względem siebie. W ogólnym przypadku, gdy kierunek wektora natężenia pola magnetycznego, wraz z kierunkiem obserwacji tworzą kąt γ, proporcje jasności poszczególnych komponentów można podać korzystając ze wzoru sformułowanego przez Fredericka H. Searesa.
Wyjaśnienie rozbicia na więcej komponentów linii widmowych plam słonecznych podał George Ellery Hale. Pomiarami polaryzacji potwierdził, że wielokrotne rozbicie linii widmowej jest następstwem zachodzenia efektu Zeemana w polu magnetycznym plamy słonecznej.
Na wykorzystaniu zjawiska Zeemana opiera się działanie magnetografu. Jest to urządzenie, przy pomocy którego można mierzyć natężenie tworzących się na Słońcu pól magnetycznych oraz ustalić ich rozprzestrzenienie.
Johannes Stark (1874–1957) niemiecki fizyk zaobserwował, że linie gazów umieszczanych w silnym polu elektrycznym także ulegają rozbiciu, podobnie jak dla efektu Zeemana. Rozbicie jest proporcjonalne do kwadratu natężenia pola. To zjawisko nazywamy efektem Starka.
Obrazy widmowe ciał niebieskich[edytuj | edytuj kod]
Słońce[edytuj | edytuj kod]
Analiza widma promieniowania słonecznego umożliwia określenie temperatury fotosfery. Zależność mocy promieniowanej przez powierzchnię ciała od jego temperatury określa prawo Stefana-Boltzmanna, tak wyliczona średnia temperatura powierzchni Słońca to 5785 K = 5512 °C. Dokładniejsze dane uzyskuje się porównując widmowy rozkład promieniowania z teoretycznym promieniowaniem ciała doskonale czarnego określonym przez Plancka. Prawo Wiena umożliwia określenie temperatury na podstawie maksimum promieniowania, dla Słońa ono wypada na 468 nm, co odpowiada światłu widzialnemu.
Obraz widmowy Słońca to spektrum ciągłe, na które nakładają się linie absorpcyjne oraz, rzadziej, emisyjne. Widmo ciągłe powstaje w fotosferze, gdyż w fotosferze ciśnienie gazu jest duże, natomiast linie absorpcyjne w znajdującej się nad nią chromosferze, w której panuje niższa temperatura oraz mniejsze ciśnienie. Obecnie znanych jest około 25 tysięcy linii absorpcyjnych w widmie słonecznym, z których ponad 75% udało się przyporządkować do określonych pierwiastków. Linie emisyjne powstają głównie w górnej warstwie atmosfery słonecznej – w koronie, w której panuje niewielkie ciśnienie i bardzo wysoka temperatura.
Zdecydowana większość tych linii znajduje się w paśmie światła widzialnego na mniejszych długościach fal. Tymczasowe linie emisyjne pojawiają się przy okazji wybuchów na Słońcu – wtedy obserwujemy znaczny wzrost temperatury. Trwa on ok. 1–2 godzin, potem linie widmowe przekształcają się w absorpcyjne.
Na podstawie natężenia linii widmowych możena ustalić skład chemiczny atmosfery słonecznej. Na podstawie danych stało się jasne, że wodór i hel, czyli 2 najlżejsze pierwiastki stanowią 97% masy Słońca, a 99,6% jeśli brać pod uwagę liczbę atomów. Oprócz sprowadzających się do atomów linii widmowych w spektrum Słońca można znaleźć także kilka pasm widmowych, które wskazują na obecność cząsteczek. W wysokiej temperaturze może być tu mowa głównie o złożeniach dwuatomowych takich jak: OH, NH, CH, SiH, MgH, CaH, C2, CN, O2, TiO, MgO, AlO. Atmosfera ziemska także zostawia swój ślad w obserwowanym spektrum Słońca. Atmosfera naszej planety będąc mieszaniną zimnych gazów, pochłania światło słoneczne o charakterystycznej dla nich długościach fal.
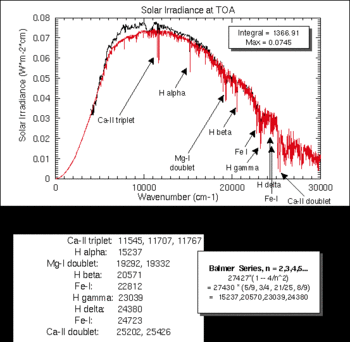
Potwierdzają to, nakładające się na widmo słoneczne, pochłaniające linie widmowe cząsteczek H2O, O2, O3, CO2, N2O, CH4, N2, które przeszkadzają w badaniu widma właściwego. Oddzielenie linii widma właściwego od tych wywoływanych przez atmoferę ziemską odbywa się na podstawie efektu Dopplera. Elementy należące do atmosfery ziemskiej mu nie ulegają i w ten sposób przy dokładnej analizie można je odróżnić od widma właściwego.
Naszą wiedzę o Słońcu zawdzięczamy w znacznej mierze dzięki narzędziom (spektroskop, spektrograf, spektrohelioskop, spektroheliograf) badającym obraz widmowy. Spektroskop służy do analizy widma, spektrografem natomiast możemy je zarejestrować, np. sfotografować. Jednakże żaden z nich nie da nam obrazu Słońca. Jeśli chcemy zobaczyć np. koronę Słońca w wybranym paśmie, lub badać właściwości jego powierzchni, a nie całą zawartość widma, wtedy używamy spekrtohelioskopu lub spektroheliografu. Te narzędzia, dzięki zabudowanemu, wyposażonemu w kratkę ekranowi, przepuszczają jedynie wybrane pasy pełnego spektrum. Oznacza to najczęściej obszar spektralny czerwonego światła widzialnego, gdyż ten obszar zdradza najwięcej o procesach zachodzących na Słońcu. Gwiazda ta składa się w większości z wodoru, którego najjaśniejsza linia widmowa to wodór-alfa. Można ją znaleźć na długości fali λ=6,5628·10−6 m. W świetle H-alfa można zaobserwować właściwości magnetyczne plam słonecznych. W wypadku dwóch sąsiadujących ze sobą plam możemy (w świetle H-alfa) ciemniejsze włókna biegnące wielkimi łukami z jednej plamy ku środkowi drugiej, wyrysowując linie pola magnetycznego.
Planety pozasłoneczne[edytuj | edytuj kod]
Obecnie dysponujemy jedynie pośrednimi metodami wykrywania planet pozasłonecznych. Może to być np. obserwowanie wpływu grawitacyjnego planety na gwiazdę którą obiega, bądź też pośrednia (spektroskopowa) obserwacja ruchu gwiazdy. Planeta jest zbyt blada w porównaniu do światła gwiazdy i krąży zbyt blisko niej, aby można było zobaczyć ją przy pomocy teleskopu, ale jej grawitacja zostawia ślady w widmie gwiazdy. Wskutek krążenia planety i gwiazdy wokół wspólnego środka masy zmienia się szybkość radialna gwiazdy: według efektu Dopplera linie widmowe przesuwają się w kierunku fioletu podczas przybliżania się do nas gwiazdy, a w wypadku oddalania się przesuwają się w stronę czerwieni. Można mierzyć te zmiany długości fali przy pomocy narzędzi spektroskopowych z dokładnością do 1 m/s. Wskutek ruchu wokół wspólnego środka masy Jowisz powoduje wahania szybkości Słońca rzędu 12 m/s, a Ziemia rzędu 0,1 m/s.
Komety, meteory, planetoidy[edytuj | edytuj kod]
Widmo komet zdradza obecność w nich cząsteczek. Emitowane przez Słońce promienie UV wywołują zjawisko fluorescencji. Widmo komy i warkocza jest w części ciągłe, co wskazuje na odbite światło słoneczne, a w części składa się z kolorowych linii emisyjnych. Przede wszystkim rozpoznajemy wśród nich linie węgla, wodoru, azotu oraz tlenu. Koma składa się z molekuł obojętnych i zjonizowanych, warkocz natomiast przeważnie ze zjonizowanych. W widmie komy można znaleźć cząsteczki CN, CH, OH, NH, C2, CH2, NH3, zjonizowane cząsteczki CO+, CO2+, OH+, CH+. W widmie warkocza natomiast pojawiają się pasy CN, CO+, CO2+, CH+ oraz N2+. Pierwsza analiza widma komety wiąże się z nazwiskiem Jean-Pierre Swingsa.
W widmie meteorów można zaobserwować przede wszystkim linie obojętnych Na, Fe, Ca, Mn, Cr, Si, Ni, Al oraz zjonizowanych Ca, Fe, Mg oraz Si. W wypadku szybkich meteorów (v > 30 km/s) dominują linie CaII, H i K. Z energii jonizacji można wyznaczyć szybkość meteoru przy wejściu w atmosferę.
Widmo planetoid (asteroid) zależy od materii pokrywającej ich powierzchnię oraz jej stanu. Na tej podstawie możemy je podzielić na:
- typ A: ekstremalnie czerwonego koloru, o silnych liniach absorpcyjnych, które wskazują na obecność oliwinu; pojawiają się rzadko
- typ B: właściwościami przypominają typ C, ale o większym albedo; rzadkie
- typ C: bardzo ciemne, ich albedo geometryczne poniżej 0,065; na powierzchni obecne są kondryty i zhydratowane (zwodnione) krzemiany; częstość występowania – 75%, głównie odległe od Słońca
- typ E: o dużym albedo, enstatyczne akondryty w topiąco-zeszkliwujących procesach; częstsze w pobliżu Słońca
- typ F: wykazują słabe linie absorpcyjne w ultrafiolecie
- typ G: przypominają typ C, ich widmo zawiera w ultrafiolecie silne linie absorpcyjne
- typ M: zbudowane z metali (żelazo, nikiel itd.); prawdopodobnie odsłonięte na skutek zderzeń jądra starych, dużych asteroid
- typ S: najbardziej heterogeniczna klasa, stosunkowo bliskie Słońca (w odległości podobnej do ziemskiej), ich albedo: 0,07–0,23, częstość występowania – 15%; składają się z różnych krzemianów, na powierzchni często dużo pyłu lub ślady procesów topnienia i krzepnięcia, które spowodowało silne promieniowanie młodego Słońca; można je dalej podzielić na siedem podklas
- typ T
- typ V: bazaltowe, krążą po dokładnie określonym torze (podobnym do toru planetoidy Vesta), są prawdopodobnie odłamkami Vesty
Gwiazdy[edytuj | edytuj kod]
Atmosferę gwiazdy – ze względu na właściwości fizyczne – dzielimy na trzy części. Fotosfera jest to najniższa warstwa atmosfery. Obok wysokiego ciśnienia i temperatury znajdziemy tu wiele swobodnych elektronów. W takich warunkach może się zdarzyć przechwycenie elektronów o najróżniejszych torach, dzięki czemu powstaje widmo ciągłe. Naturalnie mowa tu nie tylko o wodorze, ale także o cięższych, bardziej skomplikowanych atomach. Nad fotosferą rozciąga się warstwa o niższej temperaturze – chromosfera. Warstwa ta zachowuje się jak zimny gaz, pochłaniając dokładnie te wielkości energii, które są potrzebne elektronom do osiągnięcia stanu wzbudzonego. Powstają wtedy linie absorpcyjne. Nad chromosferą znajduje się korona, której grubość jest zdecydowanie większa, 106 km. Temperatura rośnie tu nagle do ogromnych wartości, osiągając rząd nawet 106 kelwinów. W takich warunkach fizycznych powstają linie emisyjne.
O różnicach w widmie gwiazd o normalnych proporcjach pierwiastków – z powodu ich podobnego składu chemicznego – decyduje przede wszystkim temperatura oraz atmosfera gwiazdy. (Dlatego w wypadku braku w widmie linii danego pierwiastka, nie wolno wnioskować o jego braku w atmosferze gwiazdy. Pierwiastek taki może się pojawiać, ale nie można zaobserwować go spektroskopowo, jeśli jego linie widmowe nie pojawiają się w znacznej liczbie w zakresach możliwych do badania z powierzchni Ziemi.) Czynnik ciśnienia wpływa głównie na szerokość linii: pod wpływem niskiego ciśnienia powstają linie wąskie i ostre, pod wpływem wysokiego – szersze. Gwiazdy wykazujące różnice w natężeniu linii widmowych porządkujemy według temperatury. Na tej podstawie opiera się system klasyfikacji widmowej Harvard. W teorii przyporządkowanie odbywa się przez ustalenie natężenia oraz szerokości połówkowej charakterystycznych, najważniejszych dla danej gwiazdy linii widmowych. Te linie/serie linii/pasy to:
- seria Balmera atomu wodoru,
- linie zjonizowanego helu i żelaza,
- linia absorpcyjna wapnia (393,3 nm),
- tzw. pas G (cząsteczka CH),
- linia obojętnego wapnia (422,7 nm),
- linie metali ok. 431 nm,
- pasy cząsteczki TiO.
Wadą tego systemu jest fakt, że nie mówi on nic o mocy promieniowania gwiazdy. Dla określenia także tego parametru wprowadzono klasyfikację spektralną Yerkes.

Ustalanie klasy widmowej gwiazdy w praktyce odbywa się następująco: Na drodze szerokokątnej kamery Schmidta umieszcza się kilkustopniowy pryzmat, w ten sposób na płytce fotograficznej pojawia się widmo wszystkich gwiazd. Rozdzielczość tak otrzymanego spektrum jest bardzo niska, nie nadaje się do szczegółowych badań, odpowiada za to regułom klasyfikacji spektralnej. Do każdej grupy przyporządkowane są tzw. gwiazdy standardowe o wzorcowym widmie. (Lista gwiazd standardowych znajduje się w artykule typ widmowy.) Przyporządkowując gwiazdę o nieznanym typie spektralnym do odpowiedniej grupy należy najpierw przygotować próbkę spektrum gwiazdy standardowej, a następnie porównać ją ze spektrum gwiazdy nieprzyporzadkowanej.
Spektroskopia astronomiczna odgrywa niezwykle ważną rolę w badaniu gwiazd spektroskopowo podwójnych. Są to takie gwiazdy podwójne, których podwójność można stwierdzić jedynie metodami spektroskopowymi. Ponieważ komponenty układu podwójnego krążą wokół wspólnego środka masy, wykazują zmiany prędkości radialnej, z wyjątkiem sytuacji, gdy płaszczyzna trajektorii ruchu komponentów jest prostopadła do kierunku patrzenia. Gdy dwa komponenty mają podobną jasność, wtedy widzimy dwa nakładające się na siebie widma, których linie poruszają się w przeciwnych kierunkach. Linie składnika zbliżającego się przesuwają się ku falom krótszym, linie elementu oddalającego się przemieszczają się ku falom dłuższym (efekt Dopplera). Po upływie czasu odpowiadającego połowie okresu obiegowego sytuacja się odwraca, natomiast, gdy gwiazdy poruszają się prostopadle do kierunku patrzenia, wtedy, naturalnie, nie obserwujemy efektu Dopplera. Podsumowując, linie widmowe gwiazd spektroskopowo podwójnych w trakcie całego okresu obrotowego dwukrotnie się rozdzielają i dwukrotnie na powrót zlewają. Dzięki obserwacji jednego pełnego cyklu oprócz czasu obiegu można także ustalić mimośrody orbit (wartość w przedziale (0,1)) oraz proporcje mas komponentów.
Materia międzygwiezdna[edytuj | edytuj kod]
| Kolor | Długość fali [nm] | Atom lub jon | Uwagi |
|---|---|---|---|
| fiolet | 372,7 | O II | zakazana linia, często mocna |
| fiolet | 386,9 | Ne III | zakazana linia |
| fiolet | 434,0 | H I | Hγ, a Hβ 40% mocności |
| niebieska zieleń | 486,1 | H I | Hβ, a Hα 30% mocności |
| zieleń | 495,9 | O III | zakazana linia |
| zieleń | 500,7 | O III | zakazana linia, często mocna |
| czerwień | 654,8 | N II | zakazana linia |
| czerwień | 656,28 | H I | Hα |
| czerwień | 658,4 | N II | zakazana linia |
Zachowanie się materii międzygwiazdowej w tym i proces powstawania z niej gwiazd jest jeszcze ciągle jednym z najbardziej niejasnych obszarów astrofizyki. Pierwsze dotyczące tego teorie wiążą się z nazwiskiem S. Laplace, którego koncepje także dziś można zauważyć we współczesnych teoriach. On pierwszy wysunął tezę, że gwiazdy – razem z planetami – tworzą się z materii międzygwiezdnej na skutek przyciągania grawitacyjnego. Na odkrycie materii międzygwiazdowej trzeba było czekać jeszcze ponad sto lat, w końcu ten rodzaj rzadkiej materii jest trudny do zaobserwowania przy pomocy urządzeń optycznych. Tak więc nie jest zaskakującym fakt, iż pierwszą bezpośrednią obserwację przeprowadzono stosunkowo późno, bo w 1904 r. J.F. Hartmann badając wtedy podwójną spektroskopowo Delta Orionis znalazł w jej widmie takie linie absorpcyjne (np. Ca), które nie brały udziału w cyklicznych przesunięciach linii spowodowanych krążeniem dwóch towarzyszy wokół wspólnego środka masy, ale pozostawały ciągle na jednej długości fali. Jedynym możliwym wyjaśnieniem, było założenie, że linie nie pochodzą od gwiazd (bo wtedy należałoby zaobserwować dla nich efekt Dopplera), tylko od będącej między gwiazdą a Ziemią materią.
Spektrum materii międzygwiezdnej to widmo ciągłe, na które nakładają się linie emisyjne. Proporcje tych dwóch składników zależą od typu pyłu; w przypadku mgławic refleksyjnych dominuje ciągłe (niebieskawe) widmo, natomiast w wypadku chmur H II, mgławic planetarnych, pozostałości po supernowych i superbąbli dominuje widmo emisyjne.
W materii międzygwiezdnej zidentyfikowano następujące indywidua chemiczne:
- dwuatomowe
- rodniki i jony: hydroksylowy (OH), aminowy (NH), wodorowęglowy (CH), krzemianowy (SiO), acetylenowy (C2), cyjanowy (CN), siarkowęglowy (CS)
- związki chemiczne: Tlenek węgla (CO), wodorek krzemu (SiH), wodorek magnezu (MgH), wodorek wapnia (CaH), tlenek tytanu (TiO), tlenek magnezu (MgO), tlenek glinu (AlO)
- a także tlen cząsteczkowy O2
- wieloatomowe: woda (H2O), cyjanowodór (HCN), formaldehyd (HCHO), HC9N, cyjanek metylu (CH3CN), metyloacetylen (CH3C2H), acetaldehyd (CH3HCO), formamid (NH2HCO), eter dimetylowy (CH3)2O.
Występowanie w przestrzeni międzygwiezdnej złożonych związków organicznych jest nie bez znaczenia dla toczących się w ramach astrobiologii dyskusji o powstawaniu życia. Okolice najbogatsze w związki chemiczne można znaleźć w gwiazdozbiorach Strzelca i Oriona.
Galaktyki[edytuj | edytuj kod]
Widmo galaktyki jest mieszanką widm jaśniejszych spośród tworzących ją gwiazd. Na kontinuum można więc zaobserwować zarówno linie absorpcyjne, jak i emisyjne. W galaktykach spiralnych pokazują się linie obszarów H II oraz chmur zjonizowanego wodoru. W ich jądrach obserwujemy bardzo szerokie linie emisyjne, które wskazują międzygwiezdny gaz o dużej szybkości (~1000 km/s). W ramionach takiej galaktyki znajdują się młode, gorące, niebieskie gwiazdy I generacji. Razem ze święcącym gazem międzygwiezdnym są one czynnikiem, dzięki któremu widzimy spiralną strukturę galaktyki. Odpowiada ona widmu typów rozciągających się od A do F. Galaktyki eliptyczne oraz jądra galaktyk spiralnych składają się z gwiazd II populacji. Obserwowane są głównie czerwone olbrzymy, które wspólnie reprezentują typy widmowe K, L i M. Odpowiednio do składu, galaktyki eliptyczne są raczej czerwone, spiralne natomiast są niebieskawe. W ich przypadku gaz i pył międzygwiezdny zbijają się w głównej płaszczyźnie w formie grubego na kilkaset parseków kręgu.
Wzajemne oddalanie się od siebie galaktyk ukazuje rozszerzanie się wszechświata. W widmie galaktyk obserwujemy przesuwanie linii ku czerwieni. Wartość przesunięcia jest tym większa, im mniejsza jest pozorna średnica lub jasność galaktyki oraz im większa jest odległość do niej. Zależność tę opisuje prawo Hubble’a.
Spektroskopia astronomiczna w praktyce. Spektrografy[edytuj | edytuj kod]
Budowa i właściwości spektrografu

Spektrografy astronomiczne są pod wieloma względami bardzo podobne do spektrografów laboratoryjnych, jednak specyfika obiektów, z jakimi mamy do czynienia w astronomii, narzuca przy ich konstruowaniu pewne dodatkowe wymagania.
Zasadę działania spektrografu można streścić następująco: teleskop zbiera światło docierające do nas od obserwowanego obiektu i kieruje je do szczeliny (lub na końcówkę światłowodu). Po wyjściu ze szczeliny (lub światłowodu) rozbieżna wiązka światła trafia na kolimator, który zamienia ją w wiązkę równoległą. Dalej światło pada na element dyspersyjny (którym jest siatka dyfrakcyjna lub pryzmat), odchylający pod różnymi kątami promienie świetlne o różnych długościach fali. Rozszczepione w ten sposób światło pada na obiektyw, który skupia je, tworząc ostry obraz widma na detektorze. Detektorem najczęściej jest matryca CCD, a w przeszłości była to klisza fotograficzna.
Ponieważ większość obiektów, z jakimi mamy do czynienia w astronomii, ma względnie małą jasność i ilość docierającego od nich światła jest bardzo niewielka, w spektroskopii astronomicznej bardzo istotne jest jak najefektywniejsze wykorzystanie niemal każdego fotonu. Osiąga się to przez optymalne dopasowanie parametrów optycznych elementów spektrografu (światłowodu, kolimatora) do teleskopu, a także przez zastosowanie odpowiednio czułych detektorów światła (niskoszumowe matryce CCD).
Jednym z głównych parametrów spektrografu jest jego rozdzielczość, definiowana jako R = λ/Δλ, gdzie λ oznacza długość fali, a Δλ najmniejszą różnicę długości fal pomiędzy elementami widma, które możemy jeszcze rozróżnić. Typowe wartości R dla spektrografów o niskiej rozdzielczości wynoszą od kilkuset do kilku tysięcy, dla wysokiej rozdzielczości (echelle) od 30 000 wzwyż (do nawet 1 000 000). Rozdzielczość wzrasta wraz ze zmniejszaniem rozmiarów szczeliny spektrografu lub średnicy światłowodu, jednak nie można jej w ten sposób zwiększać w dowolny sposób. Na przeszkodzie stoi skończoność rozmiarów obrazu gwiazdy, spowodowana efektami dyfrakcyjnymi na krawędzi obiektywu (krążek Airy’ego), a przede wszystkim efektami atmosferycznymi (seeing) – dalsze zmniejszanie rozmiarów szczeliny powodowałoby utratę coraz większej ilości światła. Należy też przy tej okazji pamiętać, że im większa rozdzielczość, tym większa musi być jasność obserwowanego obiektu, żeby przy tym samym czasie ekspozycji uzyskać satysfakcjonujący stosunek sygnału do szumu w otrzymanym widmie.
Dla uzyskania wyższej rozdzielczości zamiast zwykłych (transparentnych) siatek dyfrakcyjnych stosuje się siatki odbiciowe typu echelle, w których wykorzystywane są dalsze, z reguły dość wysokie rzędy widma. Na powierzchni takiej siatki znajdują się odpowiednio nacięte „schodki”, pokryte warstwą odbijającą światło. Szerokość i wysokość tych schodków jest dobrana w taki sposób, żeby uzyskać optymalizację odbicia dla określonych rzędów widma.
Na stabilność spektrografu ma wpływ cały szereg czynników, wśród których kluczowe znaczenie mają mechaniczne gięcia, zmiany temperatury i zmiany ciśnienia powietrza. Dawniej spektrografy instalowano albo bezpośrednio na teleskopach, albo w tzw. ognisku Coude. Obecnie w celu doprowadzenia światła z teleskopu do spektrografu coraz częściej stosuje się światłowody, co zapewnia znacznie lepszą stabilność mechaniczną. Spektrografy umieszcza się też w szczelnie zamkniętych obudowach, w których z bardzo dużą dokładnością utrzymywana jest stała temperatura. Niekiedy stosuje się nawet hermetyczne obudowy próżniowe w celu wyeliminowania wpływu zmian ciśnienia atmosferycznego (np. HARPS).
Kalibracja długości fali
Widmo uzyskane na matrycy CCD przed użyciem musi zostać skalibrowane, to znaczy musimy znaleźć odwzorowanie, które położeniu wyrażonemu w pikselach przypisuje określoną długość fali. Jeśli chcemy dokładnie mierzyć bardzo subtelne efekty, takie jak np. przesunięcia linii widmowych gwiazd spowodowane efektem Dopplera, to kalibrację taką musimy przeprowadzić szczególnie starannie.
Do kalibracji wykorzystywane są widma specjalnych lamp kalibracyjnych, zawierające dużo wąskich, dających się łatwo zmierzyć emisyjnych linii widmowych, pokrywających jak największą część kalibrowanego widma. Najczęściej używa się do tego celu lamp He-Ne (hel-neon), Th-Ar (tor-argon), He-Ne-Ar (hel-neon-argon), Fe-Ar (żelazo-argon) i innych.
Im więcej linii w widmie kalibracyjnym i im bardziej regularnie pokrywają one widmo obiektu, tym dokładniej możemy przeprowadzić kalibrację i tym większą dokładność pomiaru możemy uzyskać. W przypadku ekstremalnie małych efektów (jak np. przesunięcia dopplerowskie linii widmowych gwiazd spowodowane obecnością planety) widma klasycznych lamp kalibracyjnych mogą się okazać niewystarczające. W takich sytuacjach stosuje się obecnie coraz częściej tzw. „komórki jodowe” – przezroczyste pojemniki z jodem, umieszczone na drodze biegu promieni świetlnych pomiędzy teleskopem a spektrografem. Jod podgrzany od odpowiednio wysokiej temperatury sublimuje, a jego pary dają w widmie gęsty las cienkich linii absorpcyjnych, pozwalających bardzo znacząco zwiększyć dokładność kalibracji.
Zobacz też[edytuj | edytuj kod]
- analiza widmowa
- diagram Hertzsprunga-Russella
- efekt Dopplera
- fotometria, obok spektroskopii jedna z najskuteczniejszych metod badawczych w astronomii
- model atomu Bohra
- promieniowanie elektromagnetyczne, bardziej szczegółowo o obszarach pełnego widma elektromagnetycznego
- spektroskopia
- światło, widzialne promieniowanie elektromagnetyczne
- typ widmowy, definicje i systemy podziałów typów widmowych, lista gwiazd standardowych
Przypisy[edytuj | edytuj kod]
- ↑ spektroskopia astronomiczna, [w:] Encyklopedia PWN [dostęp 2023-11-11].
Bibliografia[edytuj | edytuj kod]
- Jacqueline Mitton: Cambridge Dictionary of astronomy (angielski).
- A. David Thackeray: Astronomical spectroscopy (angielski).
- J. Sz. Sklovszkij: Csillagok – születésük, életük, pusztulásuk (węgierski).
- Hebling János, Almási Tibor: Képalkotás és spektroszkópia THz-es sugárzással: a csillagászattól az orvosi alkalmazásokig. Magyar Tudomány 2005. 12. sz. ISSN 0025-0325 (całość tekstu [1]) (węgierski).
- Fűrész Gábor: Multiobjektum spektrográfia a modern csillagászatban. Természet Világa 2004. 4. sz. ISSN 0040-3717 (archiwum czasopisma) (węgierski).
- Veszprémi Tamás, Nyulászi László: A fotoelektron-spektroszkópia alkalmazási lehetőségei és legújabb módszerei. Magyar Kémikusok Lapja 1997. 3. sz. ISSN 0025-0163 (roczniki 1997 i 1998 [2]) (węgierski).
- Vinkó József, Szatmáry Károly, Kaszás Gábor, Kiss László: A csillagok színképe. Meteor Csillagászati évkönyv 1998 (wydany przez Magyar Csillagászati Egyesület [3]) (węgierski).
- The Messenger/El Mensajero 2002. december (wydawnictwo ESO ukazuje się co miesiąc, dostępne w internecie [4]) (angielski).
- Gázok és gőzök színképe, Bohr-posztulátumok, Franck-Hertz-kísérlet. A H-atom Bohr-modellje. uni-miskolc.hu. [zarchiwizowane z tego adresu (2012-01-21)]., Miskolci Egyetem (węgierski).
- Fűrész Gábor: CCD-kamerák a csillagászatban (węgierski).
- Vinkó József-Szatmáry Károly-Kaszás Gábor-Kiss László: A csillagok színképe, Meteor Csillagászati Évkönyv, 1998 (węgierski).
- Strona domowa SDSS (angielski).
- Spektrograf AAOmega, system 2dF (angielski).
- Astronomical spectroscopy (angielski).
- Jim Kaler: Spectra. [w:] STARS [on-line]. [dostęp 2014-07-31]. (ang.).
- Astronomical Spectroscopy University of Durnham, Centre for Advanced Instrumentation (angielski).
- Smithsonian Astrophysical Observatory, converted Multiple Mirror Telescope. cfa-www.harvard.edu. [zarchiwizowane z tego adresu (2007-02-05)]. (angielski).
- History of Astronomical Spectroscopy (angielski).
- Astronomical spectroscopy and photometry. archive.oapd.inaf.it. [zarchiwizowane z tego adresu (2014-08-08)]. (angielski).
- John Hearnshaw, Astronomical Spectrographs and their History, Cambridge University Press, 2009, ISBN 978-0-521-88257-6.






















































































