Największy wspólny dzielnik

Największy wspólny dzielnik – dla danych dwóch (lub więcej) liczb całkowitych największa liczba naturalna dzieląca każdą z nich. Pojęcie to ma wiele uogólnień, które przedstawiono w dalszej części artykułu.

Największy wspólny dzielnik liczb $a$ i $b$ zapisuje się zwykle $\mbox{nwd}(a, b)$ lub $\mbox{NWD}(a, b),$ a czasem nawet $(a, b).$ Przykładowo $\mbox{nwd}(8, 12) = 4$ oraz $\mbox{nwd}(-4, 14) = 2.$ Dwie liczby nazywa się względnie pierwszymi, jeżeli ich największym wspólnym dzielnikiem jest $1,$ względnie pierwsze są np. $9$ i $28.$

Pojęcie największego wspólnego dzielnika wykorzystuje się podczas redukcji ułamków do postaci nieskracalnej (tzn. takiej, w której licznik i mianownik są względnie pierwsze). Przykładowo największym wspólnym dzielnikiem liczb $42$ oraz $56$ jest $14,$ stąd

$\frac{42}{56} = \frac{3 \cdot 14\!\!\!\!\!\diagup}{4 \cdot 14\!\!\!\!\!\diagup} = \frac{3}{4}.$

Definicje

Jeśli nie zaznaczono inaczej, słowo „liczba” będzie oznaczać dalej liczbę całkowitą. Przedstawiona we wstępie definicja wymaga formalizacji: w szczególności należy wytłumaczyć, czym jest dzielnik liczby, co oznacza, że jest on wspólny dla danych liczb i w jaki sposób wskazać największy z nich.

Otóż liczba $a$ jest dzielnikiem liczby $b,$ jeśli istnieje taka liczba $c,$ dla której zachodzi $b = ac;$ fakt ten zapisuje się $a|b.$ Liczbę $d$ nazywa się wspólnym dzielnikiem liczb $a$ oraz $b,$ jeśli dzieli ona obie z nich.

Największym wspólnym dzielnikiem liczb $a, b,$ nazywa się taką nieujemną liczbę $d,$ oznaczaną $\mbox{nwd}(a, b),$ która jest wspólnym dzielnikiem $a$ oraz $b,$ a przy tym każdy wspólny dzielnik $a$ i $b$ dzieli $d.$ Symbolicznie można to wyrazić następująco: $d = \mbox{nwd}(a, b),$ gdy

• $d|a$ i $d|b,$ oraz
• jeśli $c|a$ i $c|b,$ to $c|d$ dla dowolnej liczby $c.$

Największy wspólny dzielnik $\mbox{nwd}(a, b)$ liczb $a$ i $b$ może być równoważnie zdefiniowany jako najmniejsza nieujemna liczba $d,$ którą można przedstawić w postaci tożsamości Bézouta:

$d = ap + bq,$

dla pewnych liczb całkowitych $p$ i $q$ – liczby te można wyznaczyć za pomocą rozszerzonego algorytmu Euklidesa.

Definicję największego wspólnego dzielnika można rozszerzyć na dowolną, skończoną liczbę argumentów za pomocą indukcji matematycznej; można go traktować jako przypadek szczególny rozszerzenia tego pojęcia na nieskończoną liczbę argumentów: największym wspólnym dzielnikiem $\mbox{nwd}(A)$ dowolnego zbioru $A$ liczb całkowitych nazywa się taką nieujemną liczbę $d,$ dla której spełnione są warunki

• $d|a$ dla każdego $a \in A,$
• jeżeli $c|a$ dla każdego $a \in A,$ to $c|d$ dla każdej liczby $c.$

Wówczas jeżeli $A$ jest zbiorem skończonym składającym się z elementów $\{a_1, a_2, \dots, a_n\},$ to największy wspólny dzielnik zbioru $A$ oznacza się symbolem $\mbox{nwd}(a_1, \dots, a_n).$

Przykłady

• Największym wspólnym dzielnikiem zbioru wszystkich liczb pierwszych jest 1.
• Największy wspólny dzielnik zbioru liczb całkowitych nie istnieje.
• Największym wspólnym dzielnikiem zbioru wszystkich tych liczb całkowitych, które w zapisie w systemie dziesiętnym jako ostatnią mają cyfrę 0, jest 10.
• Największym wspólnym dzielnikiem zbioru pustego jest $0.$ Ten przypadek szczególny bywa istotny ze względu na przejrzystość dowodów, w których unika się osobnego rozważania przypadków, gdy dany zbiór elementów jest pusty albo nie.

Obliczanie

Poprzez rozkład na czynniki pierwsze

Największe wspólne dzielniki można z zasady obliczać poprzez wyznaczenie rozkładu na czynniki pierwsze dwóch liczb i porównanie ich czynników, jak ma to miejsce w następującym przykładzie: aby obliczyć $\mbox{nwd}(18, 84)$ szuka się rozkładu na czynniki pierwsze liczb $18 = 2 \cdot 3^2$ oraz $84 = 2^2 \cdot 3 \cdot 7$ i wyodrębnia „pokrywające się” części dwóch wyrażeń, $2 \cdot 3,$ stąd $\mbox{nwd}(18, 84) = 6.$ W praktyce metoda ta jest użyteczna dla małych liczb, gdyż wyznaczanie rozkładu na czynniki pierwsze jest bardzo czasochłonne.

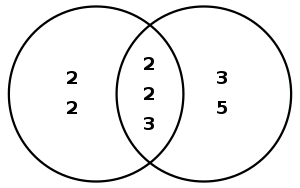
W następującym przykładzie, w którym poszukuje się największego wspólnego dzielnika liczb $48$ oraz $180,$ wykorzystany zostanie diagram Venna. Rozkładami tych liczb na czynniki pierwsze są:

$48 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3,$

$180 = 2 \cdot 2 \cdot 3 \cdot 3 \cdot 5.$

Wspólną częścią rozkładu są dwie $2$ i $3.$

Najmniejsza wspólna wielokrotność = $2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 5 = 720.$

Największy wspólny dzielnik = $2 \cdot 2 \cdot 3 = 12.$

Metoda szkolna

Dokonujemy w słupku rozkładu liczb, dla których szukamy NWD, na czynniki pierwsze rozpoczynając od czynnika 2 przez sprawdzenie, czy dana liczba dzieli się na konkretny czynnik bez reszty. Jeśli dzieli się, to pod daną liczbą wpisujemy iloraz, jeśli nie, to sprawdzamy kolejne czynniki pierwsze jako dzielniki. Dalej postępujemy analogicznie dopóki nie otrzymamy ilorazu równego 1. Następnie wyliczamy iloczyn liczby 1 i tych czynników, które występują w obu rozkładach, ale tak, że dany czynnik pierwszy w iloczynie występuje tyle razy ile razy występował w rozkładzie, w którym pojawił się mniejszą liczbę razy. Wynika z tego, że NWD dwóch liczb pierwszych jest liczba 1.

Wyznaczenie NWD liczb 42 i 56

$\begin{matrix} 42 & | & \color{red}{2} &\quad & 56 & | & 2 \\ 21 & | & 3 &\quad & 28 & | & 2 \\ 7 & | & \color{red}{7} &\quad & 14 & | & 2 \\ 1 & | & &\quad & 7 & | & 7 \\ & & &\quad & 1 & | \end{matrix}$

$\begin{matrix} NWD(42,56) = 1 \cdot (2) \cdot (7) = 14 \\ \end{matrix}$

Czynnik 2 wystąpił w obu rozkładach - raz w pierwszym rozkładzie i trzy razy w drugim, więc w iloczynie występuje tylko raz, czynnik 3 wystąpił raz w pierwszym rozkładzie i zero razy w drugim, więc w iloczynie nie występuje, natomiast czynnik 7 wystąpił jeden raz w pierwszym i drugim rozkładzie, więc w iloczynie występuje też raz.

Wyznaczenie NWD liczb 192 i 348

$\begin{matrix} 192 & | & 2 &\quad & 348 & | & \color{red}{2} \\ 96 & | & 2 &\quad & 174 & | & \color{red}{2} \\ 48 & | & 2 &\quad & 87 & | & \color{red}{3} \\ 24 & | & 2 &\quad & 29 & | & 29 \\ 12 & | & 2 &\quad & 1 & | & \\ 6 & | & 2 &\quad & & & \\ 3 & | & 3 &\quad & & & \\ 1 & | & &\quad & & & \\ \end{matrix}$

$\begin{matrix} NWD(192,348) = 1 \cdot (2\cdot2) \cdot (3) = 12 \\ \end{matrix}$

Za pomocą algorytmu Euklidesa

Znacznie bardziej efektywnym sposobem jest pochodzący ze słynnych Elementów algorytm Euklidesa, który opiera się na twierdzeniu o dzieleniu z resztą oraz obserwacji, iż $\mbox{nwd}$ dwóch liczb dzieli również ich różnicę. Przykładowo dzielenie $84$ przez $18$ daje iloraz równy $4$ i resztę $12.$ Podzielenie $18$ przez $12$ daje iloraz $1$ i resztę równą $6.$ Ostatecznie podzielenie $12$ przez $6$ daje zerową resztę, co oznacza, że $6$ jest $\mbox{nwd}.$ Formalnie można to opisać w następujący sposób:

$\mbox{nwd}(a, 0) = a,$

$\mbox{nwd}(a, b) = \mbox{nwd}\bigl(b, a - b \left\lfloor\tfrac{a}{b}\right\rfloor\bigr) = \mbox{nwd}(b, a\ \bmod\ b).$

Ciąg ilorazów powstały podczas algorytmu Euklidesa tworzy ułamek łańcuchowy.

Inne metody

Jeśli $a, b$ są niezerowe, to największy wspólny dzielnik $a$ i $b$ można obliczyć za pomocą najmniejszej wspólnej wielokrotności $\mbox{nww}$ tych liczb:

$\mbox{nwd}(a, b)= \frac{ab}{\mbox{nww}(a,b)}.$

Keith Slavin pokazał, że dla nieparzystych $a \geqslant 1$ równość

$\mbox{nwd}(a, b) = \log_2 \prod_{k=0}^{a-1} (1 + e^{-2i\pi k b/a}),$

definiuje funkcję zmiennej zespolonej $b,$ zaś Wolfgang Schramm udowodnił, że

$\mbox{nwd}(a, b) = \sum_{k=1}^a {\exp (2\pi ikb/a)} \cdot \sum_{d|a} \frac{c_d(k)}{d}$

jest funkcją całkowitą zmiennej $b$ dla wszystkich dodatnich liczb całkowitych $a,$ gdzie $c_d(k)$ oznacza sumę Ramanujana. Z kolei Marcelo Polezzi wykazał, iż

$\mbox{nwd}(a, b) = 2\sum_{k=1}^{a-1} \left\lfloor k b/a\right\rfloor + a + b - ab$

dla dodatnich liczb całkowitych $a, b.$ Donald Knuth dowiódł następującej redukcji:

$\mbox{nwd}(2^a - 1, 2^b - 1) = 2^{\mbox{nwd}(a, b)} - 1$

dla nieujemnych liczb całkowitych $a, b$ z których co najwyżej jedna może być zerem.

Własności

• Z definicji zmiana kolejności argumentów $\mbox{nwd}$ nie zmienia jego wartości.
• Każdy wspólny dzielnik liczb $a$ i $b$ jest dzielnikiem $\mbox{nwd}(a, b).$
• Dla dowolnego $a$ zachodzi $\mbox{nwd}(a, 0) = |a|,$ ponieważ każda liczba dzieli zero (jest dzielnikiem zera), zaś największym dzielnikiem $a$ jest $|a|.$ Własność ta jest punktem wyjścia dla algorytmu Euklidesa.
• Jeżeli $a|bc,$ oraz $\mbox{nwd}(a, b) = d,$ to $\tfrac{a}{d}\big|c.$
• Jeżeli $m$ jest nieujemną liczbą całkowitą, to $\mbox{nwd}(ma, mb) = m \cdot \mbox{nwd}(a, b).$
• Jeżeli $m$ jest dowolną liczbą całkowitą, to $\mbox{nwd}(a + mb, b) = \mbox{nwd}(a, b).$
• Jeżeli $m$ jest niezerowym wspólnym dzielnikiem $a$ oraz $b,$ to $\mbox{nwd}\left(\tfrac{a}{m}, \tfrac{b}{m}\right) = \tfrac{\mbox{nwd}(a, b)}{m}.$
• Jako funkcja, $\mbox{nwd}$ jest
  • multiplikatywna w następującym sensie: jeżeli $a_1$ i $a_2$ są względnie pierwsze, to $\mbox{nwd}(a_1 a_2, b) = \mbox{nwd}(a_1, b) \mbox{nwd}(a_2, b);$
  • przemienna: $\mbox{nwd}(a, b) = \mbox{nwd}(b, a);$
  • łączna: $\mbox{nwd}\bigl(a, \mbox{nwd}(b, c)\bigr) = \mbox{nwd}\bigl(\mbox{nwd}(a, b), c\bigr).$
• Największy wspólny dzielnik trzech liczb może być obliczony jako $\mbox{nwd}(a, b, c) = \mbox{nwd}\bigl(\mbox{nwd}(a, b), c\bigr)$ lub w inny sposób na mocy przemienności i łączności. Definicję tę można rozszerzyć na dowolną, skończoną liczbę argumentów.
• Liczba $\mbox{nwd}(a, b)$ jest blisko związana z najmniejszą wspólną wielokrotnością $\mbox{nww}(a, b);$ otóż

  $\mbox{nwd}(a, b) \mbox{nww}(a, b) = ab.$

Równość ta nie jest prawdziwa dla większej liczby argumentów. Wzór ten wykorzystuje się często do obliczania najmniejszych wspólnych wielokrotności: najpierw wyznacza się $\mbox{nwd}$ z algorytmu Euklidesa, a nastepnie dzieli się iloczyn danych liczb przez ich $\mbox{nwd}.$ Zachodzi następująca wersja rozdzielności:

$\mbox{nwd}\bigl(a, \mbox{nww}(b, c)\bigr) = \mbox{nww}\bigl(\mbox{nwd}(a, b), \mbox{nwd}(a, c)\bigr).$

$\mbox{nww}\bigl(a, \mbox{nwd}(b, c)\bigr) = \mbox{nwd}\bigl(\mbox{nww}(a, b), \mbox{nww}(a, c)\bigr).$

• Zdefiniowanie $\mbox{nwd}(0, 0) = 0$ oraz $\mbox{nww}(0, 0) = 0$ czyni z liczb naturalnych zupełną kratę rozdzielną z $\mbox{nwd}$ oraz $\mbox{nww}$ odpowiednio jako supremum i infimum. To rozszerzenie definicji jest zgodne z uogólnieniem na pierścienie przemienne opisanym niżej.
• W kartezjańskim układzie współrzędnych $\mbox{nwd}(a, b)$ można interpretować jako liczbę punktów o współrzędnych całkowitych leżących na prostej przechodzącej przez punkty $(0, 0)$ oraz $(a, b)$ z wyłączeniem punktu $(0, 0).$

Niech litery $A$ oraz $B$ oznaczają dowolne podzbiory liczb całkowitych. Prawdziwe są zależności:

• $1 \leqslant \mbox{nwd}(A) \leqslant \min(A).$
• $\mbox{nwd}(A \cup B) = \mbox{nwd}\bigl(\mbox{nwd}(A), \mbox{nwd}(B)\bigr).$

Uogólnienia

Prawdziwy jest następujący diagram zawierania się klas pierścieni z jedynką:

pierścienie przemienne ⊃ dziedziny całkowitości ⊃ dziedziny z jednoznacznością rozkładu ⊃ dziedziny ideałów głównych ⊃ dziedziny euklidesowe ⊃ ciała

W kontekście uogólnień największego wspólnego dzielnika poglądowo można go podsumować w następujący sposób:

• pierścień przemienny to zbiór elementów, które można dodawać, odejmować i mnożyć wg znanych reguł arytmetyki (nie zawsze istnieje iloraz dwóch elementów); w każdym pierścieniu przemiennym możliwe jest zdefiniowanie podzielności oraz $\mbox{nwd}.$
• dziedzina całkowitości to pierścień przemienny, w którym brak właściwych dzielników zera sprawia, iż struktury te są naturalnym środowiskiem do badania podzielności, a $\mbox{nwd}$ jest wyznaczony z dokładnością do stowarzyszenia (tzn. z dokładnością do elementu odwracalnego).
• dziedzina z jednoznacznością rozkładu to dziedzina całkowitości, w której zachodzi uogólnienie podstawowego twierdzenia arytmetyki, co sprawia, że dla dowolnych dwóch elementów istnieje ich $\mbox{nwd},$ przy czym można go wyznaczyć za pomocą rozkładu elementu na elementy nierozkładalne (pierwsze);
• dziedzina ideałów głównych to dziedzina z jednoznacznością rozkładu, w której dla każdych dwóch elementów $x$ i $y$ spełniona jest tzw. tożsamość Bézouta, tzn. istnieją takie elementy $a$ i $b,$ że $ax + by = \mbox{nwd}(a, b);$
• dziedzina euklidesowa to dziedzina ideałów głównych, w której poprawne zdefiniowane jest dzielenie z resztą, a $\mbox{nwd}$ można znaleźć za pomocą uogólnienia algorytmu Euklidesa.

W szczególności dziedzinami euklidesowymi są pierścień liczb całkowitych (którego największy wspólny dzielnik został opisany w zasadniczej części artykułu) oraz pierścienie wielomianów o współczynnikach z ciała, w których największym wspólnym dzielnikiem wielomianów $\mathrm f$ oraz $\mathrm g$ nazywa się wielomian unormowany (o ile, jest on różny od wielomianu zerowego; powód wyjaśniono dalej) najwyższego stopnia, który dzieli (bez reszty) $\mathrm f$ oraz $\mathrm g.$

W ciałach pojęcie największego wspólnego dzielnika (jak i największej wspólnej wielokrotności) traci sens: ponieważ każdy niezerowy element jest odwracalny, to największym wspólnym dzielnikiem dwóch niezerowych elementów jest jedynka, zatem są one względnie pierwsze; jeżeli choć jedna z nich jest zerem, to ich największym wspólnym dzielnikiem również jest zero.

Z kolei w pierścieniach nieprzemiennych sytuacja jest bardziej złożona: dla danego elementu można wyróżnić jego dzielniki lewo- i prawostronne. Można więc zdefiniować największy wspólny dzielnik lewo- i prawostronny, przy czym istnienie jednego nie pociąga za sobą istnienia drugiego, czy też ich równości w przypadku istnienia obu.

Pierścienie przemienne

Definicja korzystająca z podzielności (jak również i rozszerzona), podana w sekcji Definicje, przenosi się wprost na pierścienie przemienne. Niech $R$ będzie pierścieniem przemiennym oraz $a, b \in R.$ Element $d \in R$ nazywa się największym wspólnym dzielnikiem elementów $a, b,$ jeżeli

• $d|a$ oraz $d|b,$ oraz
• jeśli $c|a$ oraz $c|b,$ to $c|d$ dla dowolnej liczby $c.$

Jedyną różnicą jest fakt, iż nie ma gwarancji istnienia największego wspólnego dzielnika oraz tego, że jeśli nawet istnieje, to jest on wyznaczony jednoznacznie (dla danych elementów może być ich kilka; w szczególności nie zakłada się jego „nieujemności”).

Dziedziny całkowitości

W dziedzinie całkowitości $R$ największy wspólny dzielnik dwóch elementów również może nie istnieć, lecz jeśli istnieje ich kilka, to muszą być one ze sobą stowarzyszone: jeśli $d \in R$ jest $\mbox{nwd}(a, b)$ dla $a, b \in R,$ to jest nim dowolny inny element stowarzyszony z $d;$ fakt ten zapisuje się symbolicznie $d \sim \mbox{nwd}(a, b).$ Przykładowo w pierścieniu $R = \mathbb Z\left[\sqrt 2\right]$ największymi wspólnymi dzielnikami $-\sqrt 2, 5\sqrt 2$ liczb są $\sqrt 2, -\sqrt 2,$ tzn. $\sqrt 2 \sim \mbox{nwd}\left(-\sqrt 2, 5\sqrt 2\right).$

To właśnie stowarzyszenie jest powodem, dla którego największy wspólny dzielnik liczb całkowitych definiowany jest jako liczba nieujemna (w dziedzinie liczb całkowitych liczby przeciwne są ze sobą stowarzyszone, gdyż jedynymi elementami odwracalnymi są jedynka i minus jedynka), co przy tej definicji pozwala stosować znak równości $=$ zamiast znaku $\sim$ relacji stowarzyszenia. Podobnie ma się rzecz z wielomianami, gdzie jednoznaczność gwarantuje unormowanie największego wspólnego dzielnika (w pierścieniu wielomianów odwracalne są wyłącznie niezerowe elementy z ciała).

Oto przykład dziedziny całkowitości, w której dwa elementy nie mają $\mbox{nwd}:$

$R = \mathbb Z\left[\sqrt{-3}\right],\quad a = 4 = 2 \cdot 2 = \left(1 + \sqrt{-3}\right)\left(1 - \sqrt{-3}\right),\quad b = \left(1 + \sqrt{-3}\right) \cdot 2.$

Elementy $2$ oraz $1 + \sqrt{-3}$ są dwoma „maksymalnymi wspólnymi dzielnikami” (tzn. żaden wspólny dzielnik będący wielokrotnością $2$ nie jest stowarzyszony z $2,$ podobnie ma się rzecz z $1 + \sqrt{-3}),$ lecz nie są one stowarzyszone, a więc największy wspólny dzielnik $a$ oraz $b$ nie istnieje.

Dziedziny z jednoznacznością rozkładu

Niech $R$ będzie dziedziną z jednoznacznością rozkładu, zaś $P$ oznacza zbiór zawierający wyłącznie elementy pierwsze, lub też równoważnie: elementy nierozkładalne, tego pierścienia. Wówczas dowolne dwa elementy $a, b$ można zapisać w postaci skończonych iloczynów

$a \sim \prod_{p \in P} p^{\alpha_p}$

oraz

$b \sim \prod_{p \in P} p^{\beta_p},$

gdzie $(\alpha)_p$ oraz $(\beta)_p$ pewnymi ciągami liczb całkowitych, przy czym iloczyny w przedstawieniu są wyznaczone jednoznacznie z dokładnością do permutacji czynników, zaś symbol tyldy oznacza relację stowarzyszenia.

Wówczas największy wspólny dzielnik elementów $a, b$ można zdefiniować wzorem

$\mbox{nwd}(a, b) \sim \prod_{p \in P} p^{\min(\alpha_p, \beta_p)},$

co odpowiada metodzie rozkładu na czynniki proste. Skrótowo można to zapisać:

$\mbox{nwd}(P^\alpha, P^\beta) \sim P^{\min(\alpha, \beta)}.$

Najogólniejszą strukturą, w której dowolne dwa elementy mają największy wspólny dzielnik jest dziedzina z największym wspólnym dzielnikiem (ang. greatest common divisor domain) będąca dziedziną z jednoznacznością rozkładu.

Dziedziny ideałów głównych

Opierając się na tożsamości Bézouta w dowolnym pierścieniu przemiennym można rozważać zbiory elementów postaci $pa + qb,$ gdzie $p, q$ przebiegają cały pierścień. Zbiór ten jest ideałem generowanym przez $a$ oraz $b,$ który oznacza się $(a, b).$ W pierścieniu, w którym wszystkie ideały są główne (tzn. pierścieniu ideałów głównych), ideał ten pokrywałby się ze zbiorem wielokrotności pewnego elementu $d$ pierścienia; ten właśnie element nazywa się największym wspólnym dzielnikiem $a$ oraz $b.$ Tożsamość Bézouta charakteryzuje dziedziny ideałów głównych wśród klasy pierścieni noetherowskich.

Ideały

Ideał $(a, b)$ może być jednak przydatny nawet wtedy, gdy największy wspólny dzielnik $a$ i $b$ nie istnieje (rzeczywiście, Ernst Kummer wykorzystał ten ideał zamiast $\mbox{nwd}$ podczas swoich badań nad Wielkim twierdzeniem Fermata, choć widział go raczej jako zbiór pewnych hipotetycznych, czy też idealnych, elementów $d$ pierścienia, skąd właśnie nazwę wziął powyższy termin teorii pierścieni) – można go traktować jako najszersze uogólnienie pojęcia największego wspólnego dzielnika.

W związku z powyższym największy wspólny dzielnik ideałów $(a), (b)$ pierścienia $R$ definiuje się jako ideał

$\mbox{nwd}\bigl((a), (b)\bigr) = \bigl\{a + b\colon a \in (a) \mbox{ i } b \in (b)\bigr\},$

zaś ich najmniejszą wspólną wielokrotność jako ideał

$\mbox{nww}\bigl((a), (b)\bigr) = (a) \cap (b).$

Zobacz też

• liczby względnie pierwsze
• najmniejsza wspólna wielokrotność
• algorytm Euklidesa