Arytmetyka modularna

Arytmetyka modularna, arytmetyka reszt – w matematyce system liczb całkowitych, w którym liczby „zawijają się” po osiągnięciu pewnej wartości nazywanej modułem, często określanej terminem modulo (skracane mod). Pierwszy pełny wykład arytmetyki reszt przedstawił Carl Friedrich Gauss w Disquisitiones Arithmeticae („Badania arytmetyczne”, 1801).

Arytmetyka modularna pojawia się wszędzie tam, gdzie występuje powtarzalność i cykliczność; dotyczy ona samego mierzenia czasu i jako taka jest podstawą działania kalendarza (zob. dalej). Ponadto korzysta się z niej w teorii liczb, teorii grup, kryptografii, informatyce, przy tworzeniu sum kontrolnych, a nawet przy tworzeniu wzorów. Zasada działania szyfru RSA oraz test Rabina-Millera opierają się na własnościach mnożenia w arytmetyce modularnej liczb całkowitych o module wyrażającym się dużą liczbą pierwszą.

Wyraz modulo w żargonie jest używany jako „z dokładnością do”, na przykład: „Protokoły HTTP i HTTPS są identyczne modulo szyfrowanie” (tj. jedyną różnicą między http i https jest szyfrowanie).

Motywacja

Wskazania zegara 12-godzinnego jako przykład zastosowania arytmetyki modularnej.

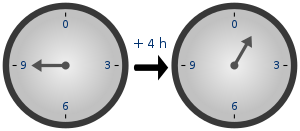
Przykładem może być zegar 24-godzinny, w którym doba podzielona jest na 24 godziny numerowane od 0 do 23. Każdej z nich można jednoznacznie przyporządkować okres w ciągu doby, który minął od godziny 0:00 do tej właśnie godziny – np. godzinie 7:00 można przyporządkować okres 7 godzin – można sobie wyobrażać, że w pewnym momencie ustawiono minutnik na 7 godzin. W ten sposób jeśli zegar wskazuje godzinę 20:00, to znaczy, że od godziny 0:00 minęło 20 godzin; podobnie jeśli zegar wskazuje godzinę 8:00, to oznacza, że godzina 0:00 była dokładnie 8 godzin temu.

Jeżeli weźmie się jednak pod uwagę okresy dłuższe niż jedna doba, to wspomniane przyporządkowanie nie jest jedynym możliwym: jeśli teraz jest godzina 0:00, to godzinę 4:00 zegar będzie wskazywać tak po 4 godzinach, jak i po 28 godzinach – ogólnie będzie on wskazywał tę samą godzinę po upływie dowolnej liczby pełnych dób (wielokrotności 24 godzin), czyli: wskazania zegara 24-godzinnego powtarzają się co 24 godziny.

Obserwacje dotyczące wskazań zegara po dwóch okresach umożliwiają określenie wskazania zegara po upływie czasu równego sumie długości tych okresów: jeżeli zegar wskazywał godzinę 0:00 i upłynęło 19 godzin (wskazuje więc on godzinę 19:00), a następnie kolejne 8 godzin (zegar nastawiony na 0:00 wskazywałby po tym czasie godzinę 8:00), to zegar nie będzie wskazywał godziny „27:00”, lecz godzinę 3:00 – tak, jak gdyby od 0:00 minęły tylko 3 godziny.

Można więc wprowadzić następujące dodawanie wskazań zegara: sumą dwóch godzin jest godzina, którą wskazywałby zegar po upływie okresu od 0:00 do pierwszej z godzin powiększonego o okres, który upłynąłby od 0:00 do drugiej z godzin. Oznacza to, że jeżeli okres jest niemniejszy niż 24 godziny, to zegar wskazywać będzie godzinę równą temu okresowi pomniejszonemu o okres 24 godzin. W ten sposób sumą godzin 12:00 i 21:00 jest godzina 9:00 (a nie 33:00). Cofaniu zegara odpowiadałyby „ujemne” okresy, tym zaś „ujemne” wskazania zegara: okresowi −7 godzin (7 godzin wstecz) odpowiada wskazanie zegara sprzed 7 godzin, gdy wskazuje on w tym momencie godzinę 0:00 – na zegarze 24-godzinnym jest to godzina 17:00. Dlatego też różnicą godzin 3:00 i 4:00 jest godzina 23:00 (a nie −1:00).

Upływ czasu liczy się więc zgodnie z arytmetyką liczb całkowitych, z kolei wskazania zegara są zgodne z arytmetyką modularną o module 24: mierzenie czasu na zegarze rozpoczyna się o godzinie 0:00 „zerując się” po osiągnięciu 24:00, z kolei gdy wskazówka zegara cofa się mijając godzinę 0:00, zegar wskazuje godzinę wcześniejszą niż 24:00.

W ten sam sposób można rozpatrywać obliczenia na dniach tygodnia (wykonywane modulo 7) lub na miesiącach (modulo 12). Prawa działań na liczbach takie jak liczba nieparzysta + liczba parzysta = liczba nieparzysta (zob. parzystość liczb) dają się opisać za pomocą arytmetyki modulo 2.

Wprowadzenie

Zgodnie z powyższą intuicją można wprowadzić w zbiorze $\{0, 1, \dots, n-1\}$ uproszczony model arytmetyki modulo $n$ definiując działania

• dodawania $\oplus_n$ wzorem

  $a \oplus_n b = \begin{cases} a + b, & \mbox{gdy } a + b < n; \\ a + b - n, & \mbox{gdy } a + b \geqslant n; \end{cases}$

• brania liczby przeciwnej $\ominus_n$ wzorem

  $\ominus_n c = \begin{cases} -c + n, & \mbox{gdy } c > 0; \\ 0, & \mbox{gdy } c = 0. \end{cases}$

W ten sposób uzyskuje się również naturalnie określone działanie

• odejmowania $a \ominus_n b := a \oplus_n (\ominus_n b)$ wzorem

  $a \ominus_n b = \begin{cases} a - b, & \mbox{gdy } a - b \geqslant 0, \mbox{ czyli } a \geqslant b; \\ a - b + n, & \mbox{gdy } a - b < 0, \mbox{ czyli } a < b.\end{cases}$

Jak zauważono wyżej dodanie wielokrotności $n$ nie zmienia wyniku działania dodawania (odejmowania) modularnego:

$(a + kn) \oplus_n b = a \oplus_n (b + kn) = a \oplus_n b$

dla dowolnych liczb całkowitych $a, b, k.$

Przykład

Działania te zgodne są intuicyjnym rozumieniem arytmetyki pomiaru czasu na zegarze 24-godzinnym: dla $n = 24$ zachodzą równości

• $7 \oplus_{24} 8 = 15,$
• $3 \ominus_{24} 13 = 3 - 13 + 24 = 14.$

Przystawanie

Dalej zamiast $a \oplus_n b$ stosowane będzie oznaczenie $[a + b]_n,$ z kolei $\ominus_n c$ będzie oznaczane $[-c]_n,$ gdzie działania dodawania i odejmowania w nawiasach kwadratowych są zwykłymi działaniami arytmetycznymi liczb całkowitych, zaś symbol $[\ ]_n$ oznaczać będzie dodanie bądź odjęcie wielokrotności liczby $n$ tak, by zawartość nawiasu należała do zbioru $\{0, \dots, n-1\}.$ Innymi słowy operacja $[c]_n$ oznacza wzięcie reszty z dzielenia liczby $c$ przez $n.$

Relację $\equiv_n$ utożsamiającą ze sobą liczby o tej samej reszcie z dzielenia przez $n,$ tzn. relację daną wzorem

$a \equiv_n b$ wtedy i tylko wtedy, gdy $[a]_n = [b]_n,$

nazywa się przystawaniem bądź kongruencją o module (modulo) $n.$ Jeśli liczby $a$ i $b$ dają tę samą resztę z dzielenia przez $n,$ to ich różnica $a - b$ jest wielokrotnością liczby $n$ lub równoważnie $n$ jest dzielnikiem $a - b$. Wspomniane dwa sformułowania są często przyjmowanymi definicjami przystawania. Innym sposobem zapisu relacji $a \equiv_n b$ jest $a = b\ (\bmod\ n),$ a nawet $a = b\ (n).$ Jeśli nie będzie prowadzić to do nieporozumień, w dalszej części artykułu indeks $n$ przy symbolach $[\ ]_n$ oraz $\equiv_n$ będzie pomijany.

W ten sposób ostatni wzór z powyższej sekcji można zapisać następująco:

$[a + b + kn] = [a + b],$

a więc

$a + b + kn \equiv a + b$

dla dowolnej liczby całkowitej $k.$ Wzór ten oznacza więc także, że przystawanie utożsamia ze sobą liczby różniące się o wielokrotność ustalonej liczby $n,$ tzn. dla każdej liczby całkowitej $c$ zachodzi

$c + kn \equiv c,$

gdzie $k$ jest dowolną liczbą całkowitą.

Przykład

Jeśli $n = 24,$ to

$57 \equiv 9,$

gdyż resztą z dzielenia 57 przez 24 oraz 9 przez 24 jest liczba 9; równoważnie

$[57] = [9],$

ponieważ $57 - 9 = 48 = 2 \cdot 24$ jest podzielne przez $24.$

W liczbach całkowitych oprócz działania dodawania i brania liczby przeciwnej (odejmowania) wyróżnione jest działanie mnożenia (w liczbach całkowitych dzielenie jest nieokreślone – w ogólności iloraz liczby całkowitej i niezerowej liczby całkowitej nie zawsze jest liczbą całkowitą, zob. wewnętrzne działanie dwuargumentowe). Oprócz działania dodawania $[a + b]$ ma więc sens rozważanie działanie mnożenia $[a \cdot b],$ można więc przyjąć

$[a \cdot b + kn] = [a \cdot b],$

czyli

$a \cdot b + kn \equiv a \cdot b.$

Skoro przystawanie utożsamia liczby różniące się o pewną wielokrotność modułu $n$ (tzn. zegar wskazuje tę samą godzinę po upływie wielokrotności 24 godzin), to można wymagać, by wynik dodawania, czy mnożenia nie zależał od wielokrotności modułu, a jedynie od reszty z dzielenia (by wynik działań na wskazaniach zegara nie zależał od czasu, który upłynął, by zegar osiągnął wskazania będące argumentami). Innymi słowy, jeśli zachodzą przystawania

$a \equiv b$ i $c \equiv d,$

to

$a + c \equiv b + d$

oraz

$ac \equiv bd.$

Dla $a \equiv b$ i dowolnej liczby całkowitej $c$ zachodzą ponadto wzory

$a \pm c \equiv b \pm c,$

gdyż $n$ dzieli $a - b = (a + c) - (b + c) = (a - c) - (b - c)$ oraz

$ac \equiv bc,$

ponieważ skoro $n$ dzieli $a - b,$ to dzieli także $c(a - b) = ac - bc.$

Powyższe wzory oznaczają więc, że kongruencje o tym samym module można dodawać, odejmować i mnożyć stronami oraz przenosić wyrazy z jednej strony kongruencji na drugą zmieniając przy tym ich znaki. Można również podnieść obie strony kongruencji do tej samej potęgi (o naturalnym wykładniku). Niepoprawne jest jednak dzielenie kongruencji stronami, ani skracanie wspólnego dla obu stron dzielnika. Jeśli $ad \equiv bd,$ to $n$ dzieli $ad - bd = d(a - b).$ Jeżeli $n$ i $d$ są względnie pierwsze, to $n$ musi dzielić $a - b,$ a więc $a \equiv b.$ Zatem dzielenie obu stron przez wspólny dzielnik jest poprawne jedynie wtedy, gdy jest on względnie pierwszy z modułem.

Pierścień klas reszt

Klasy reszt

Niech $a, b, c$ będą dowolnymi liczbami całkowitymi. Kongruencja modulo $n$ jest relacją równoważności, tzn. jest

• zwrotna:

  $a \equiv a,$

• symetryczna:

  $a \equiv b$ pociąga $b \equiv a,$

• przechodnia:

  jeśli $a \equiv b$ oraz $b \equiv c,$ to $a \equiv c.$

Jak każda relacja równoważności, przystawanie wprowadza podział zbioru (w tym wypadku liczb całkowitych) na podzbiory nazywane klasami reszt lub klasami kongruencji, które zawierają liczby dające tę samą rzesztę z dzielenia przez moduł i różniące się przy tym o jego wielokrotność; klas jest tyle, ile wynosi moduł przystawania. W dalszym ciągu podzbiory te będą oznaczane symbolem $[i],$ gdzie $i$ jest dowolną liczbą należącą do tego zbioru nazywaną reprezentantem tej klasy (zwykle jest nią najmniejsza nieujemna liczba z tego zbioru). Z własności relacji równoważności każda liczba całkowita należy do dokładnie jednej klasy reszt.

Działania

Dwie klasy reszt dodaje się wybierając z każdej z nich po jednym reprezentancie, odpowiednio $x$ oraz $y;$ wynikiem jest klasa reszt, do której należy $x + y.$ Okazuje się, że wynik takiego dodawania nie zależy od wyboru reprezentantów $x$ i $y.$

Przykład

Jeśli $n = 4,$ to klasy reszt są zbiorami:

$[0] := \{\dots, -4, 0, 4, 8, 12, \dots\},$

$[1] := \{\dots, -3, 1, 5, 9, 13, \dots\},$

$[2] := \{\dots, -2, 2, 6, 10, 14, \dots\},$

$[3] := \{\dots, -1, 3, 7, 11, 15, \dots\}.$

Chcąc dodać $[2]$ do $[3]$ wystarczy wybrać po jednym elemencie z każdej z nich, np. $2$ i $7$ – wynikiem jest klasa zawierająca $2 + 7 = 9,$ tzn. klasa $[9] = [1].$ Jeżeli wybrać przy dodawaniu $10$ i $3,$ to wynik byłby taki sam: ta sama klasa reszt zawiera liczbę $13.$

W taki sam sposób można zdefiniować mnożenie, które również jest określone jednoznacznie.

Przedstawione wyżej działania na klasach reszt mają regularne własności:

• dodawanie i mnożenie jest przemienne i łączne;
• dodawanie ma element neutralny $[0] = \{\dots, -2n, -n, 0, n, 2n, \dots\};$
• mnożenie ma element neutralny $[1] = \{\dots, -n+1, 1, n+1, 2n+1, \dots\};$
• mnożenie jest rozdzielne względem dodawania.

Struktura o tych własnościach nazywana jest pierścieniem przemiennym z jedynką.

Definicja

Niech $\equiv$ będzie relacją przystawania modulo $n,$ gdzie $n$ jest dowolną nieujemną liczbą całkowitą. Niech $[a]$ oznacza klasę abstrakcji odpowiadającą liczbie $a.$ W zbiorze ilorazowym $\mathbb Z/\equiv$ wprowadza się działania dodawania i mnożenia klas reszt (dziedziczone z pierścienia liczb całkowitych) wzorami

$[a] \oplus [b] = [a + b],$

$[a] \odot [b] = [a \cdot b].$

Zbiór $\mathbb Z/\equiv$ wraz z działaniami $\oplus$ i $\odot$ nazywa się pierścieniem klas reszt modulo $n$ i oznacza symbolami $\mathbb Z_n$ lub $\mathbb Z(n),$ przy czym działania $\oplus$ i $\odot$ zastępuje się zwykle zwyczajowymi $+$ oraz $\cdot,$ co zostanie uczynione w dalszej części artykułu. Ponadto podając elementy pierścienia $\mathbb Z_n$ opuszcza się niekiedy nawiasy i wybiera najmniejszego nieujemnego reprezentanta, tj. liczbę ze zbioru $\{0, 1, \dots, n-1\},$ którą można znaleźć biorąc resztę z dzielenia dowolnego reprezentanta przez $n.$ Innymi słowy utożsamia się w naturalny sposób elementy pierścienia $\mathbb Z_n$ z odpowiadającymi im elementami pierścienia $\mathbb Z.$

Na mocy twierdzenia o homomorfizmie dla pierścieni operator $[\ ]_n$ brania klas reszt modulo $n$ jest homomorfizmem pierścienia $\mathbb Z$ w pierścień $\mathbb Z_n,$ który przypisuje liczbie całkowitej jej resztę z dzielenia przez $n.$ Jądrem tego homomorfizmu jest ideał $n\mathbb Z,$ czyli wszystkie liczby podzielne przez $n,$ zaś obrazem są liczby ze zbioru $\{0, \dots, n-1\}.$ To samo twierdzenie o homomorfizmie zapewnia, że iloraz $\mathbb Z$ przez $n\mathbb Z$ jest izomorficzny z wyżej zdefiniowanym pierścieniem klas reszt modulo $n.$ Stąd też pochodzi alternatywne oznaczenie $\mathbb Z/n\mathbb Z$ tego pierścienia; ponieważ ideał $n\mathbb Z$ oznacza się również symbolem $(n),$ to spotyka się również oznaczenie $\mathbb Z/(n).$ W ten sposób konstrukcje dzielenia pierścienia liczb całkowitych przez relację przystawania modulo $n$ i dzielenia go przez ideał $n\mathbb Z$ są równoważne z punktu widzenia algebry.

Pierścień $\mathbb Z_0$ jest izomorficzny z pierścieniem $\mathbb Z,$ przypadek ten omawia się szerzej w artykule dotyczącym liczb całkowitych.

Własności

Elementem neutralnym dodawania w $\mathbb Z_n$ jest $[0],$ elementem przeciwnym do $[k]$ jest $[-k] = [n-k],$ elementem neutralnym mnożenia jest $[1].$

Element $[k]$ pierścienia $\mathbb Z_n$ jest odwracalny wtedy i tylko wtedy, gdy liczba całkowita $k$ jest względnie pierwsza z $n.$ Wynika to z faktu, iż można dobrać takie liczby całkowite $a, b,$ dla których zachodzi $an + bk = 1;$ wtedy $bk \equiv 1,$ czyli $[b][k] = 1,$ co oznacza, iż $[k]$ ma odwrotność $[b].$ Jeżeli $n$ i $k$ mają wspólny dzielnik $a > 1,$ tj. $n = ab,$ i $k = ac,$ to $[k][b] = [ac][b] = [abc] = 0,$ co oznacza, że $[k]$ jest dzielnikiem zera.

Wynika stąd, że jeżeli $n$ jest liczbą pierwszą, to w pierścieniu $\mathbb Z_n$ jedynym dzielnikiem zera jest $[0].$ W przeciwnym wypadku istnieją nietrywialne dzielniki zera. Dlatego pierścień $\mathbb Z_n$ jest ciałem wtedy i tylko wtedy, gdy $n$ jest liczbą pierwszą.

Charakterystyka pierścienia $\mathbb Z_n$ jest równa $n.$ Każdą grupę abelową o skończonej liczbie generatorów można przedstawić jako sumę prostą grup $\mathbb Z_n$ (zob. twierdzenie).

Grupa addytywna

Grupa addytywna pierścienia $(\mathbb Z_n, +, \cdot),$ tj. $(\mathbb Z_n, +)$ jest grupą cykliczną zwaną addytywną grupą klas reszt modulo $n.$ W teorii grup oznacza się ją symbolami $\mathbb Z_n$ lub $\mathbb Z/n\mathbb Z.$

Generatorem tej grupy jest dowolna liczba względnie pierwsza z $n$. Co więcej, z dokładnością do izomorfizmu, jedynymi grupami cyklicznymi są $(\mathbb Z_n, +, \cdot)$ i grupa addytywna liczb całkowitych.

Prawdziwa jest też równość dotycząca rzędu elementu:

$\operatorname{o}(g) = \tfrac{n}{\operatorname{nwd}(g, n)},$

gdzie $\operatorname{nwd}$ oznacza największy wspólny dzielnik.

Grupa multyplikatywna

Elementami odwracalnymi pierścienia $\mathbb Z_n$ są te liczby ze zbioru $\{0, 1, \dots, n-1\},$ które są względnie pierwsze z $n$:

$\mathbb{Z}_n^* = \big\{[a]\colon \operatorname{nwd}(a, n) = 1\big\}.$

Ich liczbę wyznacza funkcja φ Eulera. W szczególności, $\varphi(n) = n-1 \Leftrightarrow n \in \mathbb P \Leftrightarrow \mathbb Z_n$ jest ciałem.

Te elementy tworzą grupę, zwaną multiplikatywną grupą klas reszt modulo $n.$ Oznaczana jest $\mathbb Z_n^*,$ $U(\mathbb Z_n)$ lub $(\mathbb Z/n\mathbb Z)^*$.

Element $a$ jest generatorem grupy $\mathbb Z_n^*$ wtedy i tylko wtedy, gdy liczba $a$ jest pierwiastkiem pierwotnym liczby $n$. Grupa $\mathbb Z_n^*$ jest zatem cykliczna wtedy i tylko wtedy, gdy liczba $n$ posiada pierwiastek pierwotny, a to zachodzi dokładnie wtedy, gdy $n= 2, 4$, gdy $n$ jest potęgą nieparzystej liczby pierwszej (to znaczy postaci $p^\alpha$, $p$-nieparzysta liczba pierwsza) lub podwojoną potęgą nieparzystej liczby pierwszej (to znaczy postaci $2p^\alpha$, $p$-nieparzysta liczba pierwsza) . Tak więc grupa $\mathbb Z_n^*$ jest cykliczna dla $n=2,3,4,5,6,7,9,10,11,13,14,17,18,19,22,23,25,26,27,29,31$ itd.

Pierwiastki kwadratowe z jedności

Pierwiastkiem kwadratowym z jedności modulo $n$ nazywa się taki element $k \in \mathbb Z_n,$ dla którego zachodzi

$k^2 = 1.$

W dowolnym pierścieniu $\mathbb Z_n$ pierwiastkami z jedności są $1$ i $-1.$ Można udowodnić, że liczba wszystkich pierwiastków kwadratowych modulo $n$ wynosi

$2^{f(n)+[8|n]-[2|n]+[4|n]}\,$

gdzie:

• $[x|y]$ jest równe 1, gdy $x$ jest dzielnikiem $y,$ 0, jeżeli nie jest;
• $f(n)$ jest liczbą pierwszych dzielników $n$.

Aby sprawdzić, czy równanie $a^2=x$ ma rozwiązanie, można skorzystać z własności symbolu Jacobiego.

Przykład

W pierścieniu $\mathbb Z_{60}$ jest $2^{3 + 0 - 1 + 1} = 2^3 = 8$ pierwiastków z jedynki:

• $1 \mapsto 1^2 \equiv 1,$
• $11 \mapsto 11^2 = 121 \equiv 1,$
• $19 \mapsto 19^2 = 361 \equiv 1,$
• $29 \mapsto 29^2 = 841 \equiv 1,$
• $31 \mapsto 31^2 \equiv (-29)^2 \equiv 1,$
• $41 \mapsto 41^2 \equiv (-19)^2 \equiv 1,$
• $49 \mapsto 49^2 \equiv (-11)^2 \equiv 1,$
• $59 \mapsto 59^2 \equiv (-1)^2 \equiv 1.$

Zobacz też

• cecha podzielności,
• małe twierdzenie Fermata,
• Blum Blum Shub,
• logarytm dyskretny.

Bibliografia

• Ronald L. Graham, Donald E. Knuth, Oren Patashnik: Matematyka konkretna. Warszawa: Wydawnictwo Naukowe PWN, 2006. ISBN 83-01-14764-4.