Hiperbola (matematyka)

Hiperbole sprzężone

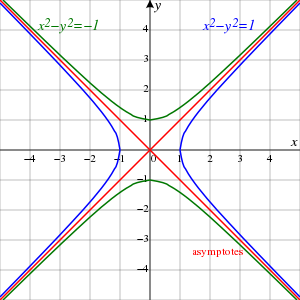
Hiperbola (stgr. ὑπερβολή hyperbolḗ „przerzucenie; przesada”) – krzywa będąca zbiorem takich punktów, dla których wartość bezwzględna różnicy odległości tych punktów od dwóch ustalonych punktów – nazywanych ogniskami hiperboli – jest stała.

Hiperbola jest zarazem krzywą stożkową, dla której kąt pomiędzy płaszczyzną tnącą a osią stożka jest mniejszy od kąta pomiędzy osią stożka a jego tworzącą.

Jeżeli ogniska hiperboli mają współrzędne $(-c,0)$ i $(c,0),$ to można ją opisać równaniem:

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,$

gdzie $a$ jest połową odległości pomiędzy wierzchołkami hiperboli, natomiast $b$ jest połową odległości pomiędzy wierzchołkami urojonymi. Zachodzi również związek:

$b^{2}=c^{2}-a^{2}.$

Jeżeli $a=b,$ to hiperbola nazywana jest równoosiową.

Mimośrodem hiperboli nazywa się stosunek odległości pomiędzy ogniskami a wierzchołkami rzeczywistymi:

$e={\frac {2c}{2a}}={\frac {c}{a}}>1.$

Od mimośrodu zależy kształt hiperboli.

Kierownicami hiperboli nazywa się proste wyrażone równaniami

$x=\pm {\frac {a}{e}}=\pm {\frac {a^{2}}{c}}.$

Obierając na hiperboli dowolny punkt $P=(x,y),$ przez $r_{1}$ oznacza się odległość pomiędzy tym punktem a lewym ogniskiem, natomiast przez $r_{2}$ odległość pomiędzy punktem $P$ a prawym ogniskiem. Wtedy mają miejsce następujące związki:

• dla prawej gałęzi: $r_{1}=a+ex,\ \ r_{2}=-a+ex,$
• dla lewej gałęzi: $r_{1}=-a-ex,\ \ r_{2}=a-ex.$

Niech $d_{1}$ będzie odległością ustalonego punktu $P$ od lewej kierownicy, a $d_{2},$ odpowiednio – od prawej. Wówczas:

${\frac {r_{1}}{d_{1}}}={\frac {r_{2}}{d_{2}}}=e.$

Hiperbolę o równianiu

$-{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

nazywa się hiperbolą sprzężoną (do wyjściowej hiperboli). Hiperbola i hiperbola do niej sprzężona mają wspólne asymptoty o równaniach

$y=\pm {\frac {b}{a}}x.$

Odcinek, który przechodzi przez środek hiperboli, a jego końce na niej leżą nazywany jest średnicą hiperboli.

Styczna w punkcie $Q=(p,q)$ hiperboli spełnia równanie

${\frac {px}{a^{2}}}-{\frac {qy}{b^{2}}}=1.$

Zobacz też

• radionawigacja
• twierdzenie Pascala

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Hyperbola, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).