Funkcje hiperboliczne

Funkcje hiperboliczne – funkcje zmiennej rzeczywistej lub zespolonej będących sumą, różnicą lub ilorazem funkcji wykładniczych określone następująco:

• sinus hiperboliczny: $\sinh x={\frac {e^{x}-e^{-x}}{2}}$ (oznaczany również $\operatorname {sh} x$),

• cosinus hiperboliczny: $\cosh x={\frac {e^{x}+e^{-x}}{2}}$ (oznaczany również $\operatorname {ch} x$),

• tangens hiperboliczny: $\operatorname {tgh} x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$ (oznaczany również $\operatorname {th} x$ lub $\tanh x$),

• cotangens hiperboliczny: $\operatorname {ctgh} x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}$ (oznaczany również $\operatorname {cth} x$ lub $\coth x$),

• secans hiperboliczny: $\operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}},$
• cosecans hiperboliczny: $\operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}.$

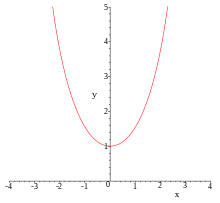
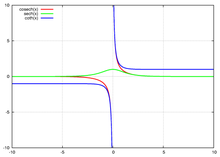
Funkcje te mają interesujące własności matematyczne analogiczne do własności funkcji trygonometrycznych. Nazwę swoją zawdzięczają temu, że para liczb (cosh(t),sinh(t)) tworzy wykres hiperboli $x^{2}-y^{2}=1$ (jej prawej, dodatniej części). Zostały wprowadzone do nauki przez włoskiego matematyka Vincenzo Riccatiego, który publikował swoje rozważania w Opusculorum ad res physicas et mathematicas pertinentium, wydawanym między 1757 a 1762 rokiem. Nadał im on nazwy sinus i cosinus hiperbolico i zastosował skróty Sh i Ch, stosowane do dziś w Rosji i we Francji. Upowszechnił je szwajcarski matematyk Johann Heinrich Lambert, pokazując ich zastosowanie w trygonometrii w dziele Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques (1762). Lambert zostawił im nazwy zaproponowane przez Riccatiego, ale nadał im skróty sinh i cosh stosowane do dnia dzisiejszego.

Związki trygonometryczne

Zbiór punktów płaszczyzny o współrzędnych postaci $(\cos x,\sin x)$ jest okręgiem (jednostkowym), analogicznie zbiór punktów o współrzędnych postaci $(\cosh x,\sinh x)$ wyznacza hiperbolę.

Prawdziwe są również wzory:

$\sinh 2t=2\sinh t\cosh t,$

$\cosh 2t=\cosh ^{2}t+\sinh ^{2}t,$

$\sinh x+\cosh x=e^{x}.$

Ponadto korzystając ze wzoru Eulera

$e^{ix}=\cos x+i\sin x,$

można przedstawić związek funkcji hiperbolicznych z trygonometrycznymi, wyrażony w liczbach zespolonych:

$\sinh ix=i\sin x,$

$\cosh ix=\cos x,$

$\operatorname {tgh} ix=i\operatorname {tg} x,$

$\operatorname {ctgh} ix=-i\operatorname {ctg} x,$

skąd:

$\sinh x=-i\sin ix,$

$\cosh x=\cos ix,$

$\operatorname {tgh} x=-i\operatorname {tg} ix,$

$\operatorname {ctgh} x=i\operatorname {ctg} ix.$

Ponieważ funkcje trygonometryczne są okresowe wzdłuż osi liczb rzeczywistych, to funkcje hiperboliczne są okresowe wzdłuż osi liczb urojonych z okresem $2\pi i$ (sinh, cosh, sech, csech), albo $\pi i$ (tgh, ctgh).

Właściwości

• Sinus hiperboliczny jest funkcją nieparzystą i funkcją rosnącą.
• Cosinus hiperboliczny jest funkcją parzystą i funkcją rosnącą dla $x>0$ i malejącą dla $x<0.$
• Tangens hiperboliczny jest funkcją nieparzystą.

Jeśli $\varphi$ oznacza złotą proporcję, to:

• $\sinh \ln \varphi ={\tfrac {1}{2}},$
• $\cosh \ln \varphi ={\tfrac {1}{2}}{\sqrt {5}}.$

Zależności hiperboliczne

Odpowiednikiem wzoru jedynkowego $\sin ^{2}x+\cos ^{2}x=1$ jest tzw. „jedynka hiperboliczna”:

$\cosh ^{2}x-\sinh ^{2}x=1.$

Z każdej tożsamości trygonometrycznej można otrzymać tożsamość hiperboliczną przez użycie związku pomiędzy funkcjami trygonometrycznymi i hiperbolicznymi.

Pochodne i całki

$\sinh 'x=\cosh x,$

$\cosh 'x=\sinh x,$

$\operatorname {tgh} 'x={\frac {1}{\cosh ^{2}x}}=1-{\operatorname {tgh} ^{2}x},$

$\operatorname {ctgh} 'x={\frac {-1}{\sinh ^{2}x}}=1-{\operatorname {ctgh} ^{2}x}.$

Rozwinięcia

Szeregi potęgowe

$\sinh z=\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{(2n+1)!}}=z+{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}+{\frac {z^{7}}{7!}}+\dots ,$

$\cosh z=\sum _{n=0}^{\infty }{\frac {z^{2n}}{(2n)!}}=1+{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}+{\frac {z^{6}}{6!}}+\cdots .$

Iloczyny nieskończone

$\sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),$

$\cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right).$

Funkcje odwrotne

Funkcje hiperboliczne mają funkcje odwrotne zwane funkcjami polowymi (lub area). Są one wyrażone przez logarytmy. Funkcją odwrotną do sinh jest area sinus hiperboliczny, do cosh area cosinus hiperboliczny itd.

Wykresy

Oto wykres funkcji sinh:

Wykres funkcji cosh ma kształt krzywej łańcuchowej:

Zobacz też

• złota funkcja

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Hyperbolic Functions, [w:] MathWorld [online], Wolfram Research [dostęp 2020-12-12]  (ang.).