Rzut lub projekcja [a] rzutu znanego z geometrii elementarnej: idempotentny endomorfizm liniowy określony na danej przestrzeni liniowej , czyli operator liniowy zachowujący swój obraz , tzn. dla którego każdy element obrazu jest punktem stałym tego przekształcenia.
Rzuty/projekcje ortogonalne są uogólnieniem pojęcia rzutu prostokątnego z geometrii euklidesowej (zob. osobna sekcja ); w przestrzeniach unitarnych (tzn. z iloczynem skalarnym , np. przestrzeniach euklidesowych ) są to nie mniej, nie więcej operatory samosprzężone .
Rzut
T
{\displaystyle \mathrm {T} }
k
{\displaystyle k}
m
.
{\displaystyle m.}
Niech dana będzie przestrzeń liniowa
V
{\displaystyle V}
ciałem ). Przekształcenie liniowe
P
:
V
→
V
{\displaystyle \mathrm {P} \colon V\to V}
warunek idempotentności
P
2
=
P
,
{\displaystyle \mathrm {P} ^{2}=\mathrm {P} ,}
czyli
P
(
P
(
v
)
)
=
P
(
v
)
{\displaystyle \mathrm {P} {\big (}\mathrm {P} (\mathbf {v} ){\big )}=\mathrm {P} (\mathbf {v} )}
v
∈
V
{\displaystyle \mathbf {v} \in V}
rzutem (ukośnym) lub projekcją .
Odwzorowanie
P
{\displaystyle \mathrm {P} }
v
∈
V
{\displaystyle \mathbf {v} \in V}
v
=
w
+
u
,
{\displaystyle \mathbf {v} =\mathbf {w} +\mathbf {u} ,}
w
∈
ker
P
{\displaystyle \mathbf {w} \in \ker \mathrm {P} }
u
∈
i
m
P
{\displaystyle \mathbf {u} \in \mathrm {im\;P} }
[b]
V
=
ker
P
⊕
i
m
P
,
{\displaystyle V=\ker \mathrm {P} \oplus \mathrm {im\;P} ,}
V
{\displaystyle V}
sumą prostą jądra i obrazu
P
.
{\displaystyle \mathrm {P} .}
V
{\displaystyle V}
U
{\displaystyle U}
podprzestrzenią liniową , to na mocy twierdzenia o rzędzie istnieje rzut
P
,
{\displaystyle \mathrm {P} ,}
i
m
P
=
U
{\displaystyle \mathrm {im\;P} =U}
0
<
dim
U
<
dim
V
,
{\displaystyle 0<\dim U<\dim V,}
V
{\displaystyle V}
U
{\displaystyle U}
Dla danych podprzestrzeni
W
,
U
{\displaystyle W,U}
V
{\displaystyle V}
V
=
W
⊕
U
{\displaystyle V=W\oplus U}
P
:
V
→
V
{\displaystyle \mathrm {P} \colon V\to V}
rzutem na
U
{\displaystyle U}
W
,
{\displaystyle W,}
v
∈
V
{\displaystyle \mathbf {v} \in V}
P
(
v
)
∈
U
{\displaystyle \mathrm {P} (\mathbf {v} )\in U}
v
−
P
(
v
)
∈
W
.
{\displaystyle \mathbf {v} -\mathrm {P} (\mathbf {v} )\in W.}
Jedynymi wartościami własnymi rzutu są zero i jedynka, tzn. widmo rzutu
P
{\displaystyle \mathrm {P} }
σ
(
P
)
=
{
0
,
1
}
{\displaystyle \sigma (\mathrm {P} )=\{0,1\}}
[c] diagonalizowalny i w szczególności (w ciele charakterystyki zerowej) jego ślad jest równy wymiarowi obrazu [d]
A
{\displaystyle \mathrm {A} }
σ
(
A
)
=
{
0
,
1
}
{\displaystyle \sigma (\mathrm {A} )=\{0,1\}}
A
{\displaystyle \mathrm {A} }
[e]
Jeśli
P
{\displaystyle \mathrm {P} }
U
{\displaystyle U}
W
,
{\displaystyle W,}
Q
=
I
−
P
:
V
→
V
{\displaystyle \mathrm {Q} =\mathrm {I} -\mathrm {P} \colon V\to V}
Q
(
v
)
=
v
−
P
(
v
)
{\displaystyle \mathrm {Q} (\mathbf {v} )=\mathbf {v} -\mathrm {P} (\mathbf {v} )}
W
{\displaystyle W}
U
{\displaystyle U}
[f]
V
=
U
⊕
W
{\displaystyle V=U\oplus W}
P
,
Q
.
{\displaystyle \mathrm {P} ,\mathrm {Q} .}
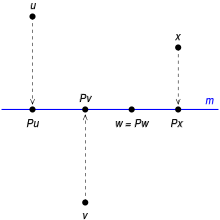
Rzut ortogonalny
P
{\displaystyle \mathrm {P} }
m
.
{\displaystyle m.}
Jeżeli
P
{\displaystyle \mathrm {P} }
U
{\displaystyle U}
W
{\displaystyle W}
V
=
W
⊥
U
{\displaystyle V=W\perp U}
ortogonalną sumą prostą , to
P
{\displaystyle \mathrm {P} }
rzutem ortogonalnym (na
U
{\displaystyle U}
W
{\displaystyle W}
W
=
U
⊥
{\displaystyle W=U^{\perp }}
dopełnieniem ortogonalnym
U
,
{\displaystyle U,}
V
=
U
⊥
⊕
U
,
{\displaystyle V=U^{\perp }\oplus U,}
V
=
(
i
m
P
)
⊥
⊕
i
m
P
,
{\displaystyle V=(\mathrm {im\;P} )^{\perp }\oplus \mathrm {im\;P} ,}
ker
P
=
(
i
m
P
)
⊥
,
{\displaystyle \ker P=(\mathrm {im\;P} )^{\perp },}
i
m
P
{\displaystyle \mathrm {im\;P} }
ker
P
{\displaystyle \ker \mathrm {P} }
obraz i jądro rzutu
P
.
{\displaystyle \mathrm {P} .}
Konstrukcja ortogonalnej sumy prostej wymaga istnienia (niezdegenerowanej) symetrycznej formy dwuliniowej określonej na przestrzeni (tzw. przestrzeń ortogonalna ): zwykle rozważa się przestrzenie z iloczynem skalarnym (tzw. przestrzenie unitarne ); w przypadku przestrzeni nieskończonego wymiaru zakłada się dodatkowo zupełność , co sprawia, że przestrzeń unitarna
V
{\displaystyle V}
przestrzenią Hilberta – istnienie zapewnia wtedy twierdzenie o rzucie ortogonalnym . W tym kontekście rzut ukośny nazywa się operatorem idempotentnym , a rzut ortogonalny znany jest jako operator rzutowy .
Rzut jest ortogonalny wtedy i tylko wtedy, gdy jest i) samosprzężony [g] normalny lub iii) dodatni (dodatnio określony) lub iv) izometryczny . Rzuty ortogonalne są operatorami ograniczonymi (czyli ciągłymi ), a gdy są nietrywialne: o jednostkowej normie operatorowej [h]
A
{\displaystyle \mathrm {A} }
A
∗
A
=
A
.
{\displaystyle \mathrm {A} ^{*}\mathrm {A} =\mathrm {A} .}
Gdy rozważana przestrzeń jest zespolona , gwiazdkę przy oznaczeniu macierzy należy interpretować jako sprzężenie hermitowskie , w pozostałych przypadkach – jako transpozycję ; w przypadku przekształceń gwiazdka oznacza (antyliniowe ) przekształcenie sprzężone do danego. Jeśli
u
1
,
…
,
u
k
{\displaystyle \mathbf {u} _{1},\dots ,\mathbf {u} _{k}}
bazą ortonormalną podprzestrzeni
U
{\displaystyle U}
A
{\displaystyle \mathbf {A} }
n
×
k
,
{\displaystyle n\times k,}
u
1
,
…
,
u
k
,
{\displaystyle \mathbf {u} _{1},\dots ,\mathbf {u} _{k},}
P
A
=
A
A
∗
{\displaystyle \mathbf {P} _{\mathbf {A} }=\mathbf {AA} ^{*}}
i reprezentuje ona przekształcenie, które można zapisać jako[i]
P
A
(
⋅
)
=
∑
i
=
1
k
u
i
⟨
u
i
,
⋅
⟩
.
{\displaystyle \mathrm {P} _{\mathrm {A} }(\cdot )=\sum _{i=1}^{k}\mathbf {u} _{i}\langle \mathbf {u} _{i},\cdot \rangle .}
W szczególności rzut na prostą (przestrzeń jednowymiarową) rozpinaną przez wektor jednostkowy
u
{\displaystyle \mathbf {u} }
P
u
(
⋅
)
=
u
⟨
u
,
⋅
⟩
,
{\displaystyle \mathrm {P} _{\mathbf {u} }(\cdot )=\mathbf {u} \langle \mathbf {u} ,\cdot \rangle ,}
P
u
=
u
u
∗
{\displaystyle \mathbf {P} _{\mathbf {u} }=\mathbf {uu} ^{*}}
[j]
Macierz
A
∗
{\displaystyle \mathbf {A} ^{*}}
izometrię częściową
A
∗
,
{\displaystyle \mathrm {A} ^{*},}
U
,
{\displaystyle U,}
A
{\displaystyle \mathrm {A} }
izometrią , która zanurza
U
{\displaystyle U}
V
.
{\displaystyle V.}
Warunek ortonormalności można opuścić; jeżeli
u
1
,
…
,
u
k
{\displaystyle \mathbf {u} _{1},\dots ,\mathbf {u} _{k}}
bazą (niekoniecznie ortonormalną), a macierz
A
{\displaystyle \mathbf {A} }
[k]
P
A
=
A
(
A
∗
A
)
−
1
A
∗
.
{\displaystyle \mathbf {P} _{\mathbf {A} }=\mathbf {A} (\mathbf {A} ^{*}\mathbf {A} )^{-1}\mathbf {A} ^{*}.}
Reprezentowane przez tę macierz przekształcenie nadal zanurza
U
{\displaystyle U}
V
,
{\displaystyle V,}
Przekształcenie liniowe , którego macierz ma postać
[
1
0
0
0
]
,
{\displaystyle \left[{\begin{smallmatrix}1&0\\0&0\end{smallmatrix}}\right],}
[
0
1
0
1
]
{\displaystyle \left[{\begin{smallmatrix}0&1\\0&1\end{smallmatrix}}\right]}
Przestrzeń
L
2
(
R
)
{\displaystyle \mathrm {L} ^{2}(\mathbb {R} )}
całkowalnych z kwadratem (w sensie Lebesgue’a ) jest ortogonalną sumą prostą przestrzeni
M
,
N
{\displaystyle M,N}
funkcji parzystych i nieparzystych ; rzuty
P
M
,
P
N
{\displaystyle \mathrm {P} _{M},\mathrm {P} _{N}}
M
,
N
{\displaystyle M,N}
[l]
P
M
f
(
x
)
=
f
(
x
)
+
f
(
−
x
)
2
oraz
P
N
f
(
x
)
=
f
(
x
)
−
f
(
−
x
)
2
,
{\displaystyle \mathrm {P} _{M}f(x)={\tfrac {f(x)+f(-x)}{2}}\qquad {\text{ oraz }}\qquad \mathrm {P} _{N}f(x)={\tfrac {f(x)-f(-x)}{2}},}
przy czym
I
−
P
M
=
P
N
.
{\displaystyle \mathrm {I} -\mathrm {P} _{M}=\mathrm {P} _{N}.}
Niech
A
{\displaystyle A}
zbiorem mierzalnym
R
,
{\displaystyle \mathbb {R} ,}
przedziałem , z funkcją charakterystyczną
χ
A
.
{\displaystyle \chi _{A}.}
[l]
P
A
f
(
x
)
=
χ
A
(
x
)
f
(
x
)
{\displaystyle \mathrm {P} _{A}f(x)=\chi _{A}(x)f(x)}
L
2
(
R
)
{\displaystyle \mathrm {L} ^{2}(\mathbb {R} )}
nośniku zawartym w domknięciu
A
¯
.
{\displaystyle {\overline {A}}.}
Zamiast wspomnianej wcześniej przestrzeni Hilberta
R
n
{\displaystyle \mathbb {R} ^{n}}
P
u
(
x
)
=
u
u
∗
x
{\displaystyle \mathrm {P} _{\mathbf {u} }(\mathbf {x} )=\mathbf {uu} ^{*}\mathbf {x} }
przestrzeni ciągów
ℓ
2
(
Z
)
,
{\displaystyle \ell ^{2}(\mathbb {Z} ),}
u
=
e
n
,
{\displaystyle \mathbf {u} =\mathbf {e} _{n},}
e
n
=
(
δ
k
,
n
)
k
=
−
∞
+
∞
{\displaystyle \mathbf {e} _{n}=\left(\delta _{k,n}\right)_{k=-\infty }^{+\infty }}
[m]
x
=
(
x
k
)
,
{\displaystyle \mathbf {x} =(x_{k}),}
P
e
n
(
x
)
=
x
n
e
n
.
{\displaystyle \mathrm {P} _{\mathbf {e} _{n}}(\mathbf {x} )=x_{n}\mathbf {e} _{n}.}
Jeśli z kolei dana jest przestrzeń
L
2
(
T
)
{\displaystyle \mathrm {L} ^{2}(\mathbb {T} )}
przestrzenią funkcji o okresie
2
π
{\displaystyle 2\pi }
[n]
u
=
1
/
2
π
{\displaystyle u=1/{\sqrt {2\pi }}}
funkcją stałą o jednostkowej normie, to rzut ortogonalny
P
u
{\displaystyle \mathrm {P} _{u}}
f
{\displaystyle f}
średnią
⟨
f
⟩
,
{\displaystyle \langle f\rangle ,}
⟨
f
⟩
=
1
2
π
∫
0
2
π
f
(
x
)
d
x
.
{\displaystyle \langle f\rangle ={\frac {1}{2\pi }}\int _{0}^{2\pi }\!\!f(x)\ \mathrm {d} x.}
Odpowiadający temu rzutowi rozkład ortogonalny,
f
(
x
)
=
⟨
f
⟩
+
f
′
(
x
)
,
{\displaystyle f(x)=\langle f\rangle +f'(x),}
⟨
f
⟩
{\displaystyle \langle f\rangle }
f
′
{\displaystyle f'}
↑ Etymologia w artykule projekcja .
↑ Wystarczy przyjąć
u
=
P
(
v
)
{\displaystyle \mathbf {u} =\mathrm {P} (\mathbf {v} )}
w
=
v
−
u
,
{\displaystyle \mathbf {w} =\mathbf {v} -\mathbf {u} ,}
P
(
w
)
=
P
(
v
−
P
(
v
)
)
=
P
(
v
)
−
P
2
(
v
)
=
P
(
v
)
−
P
(
v
)
=
0
.
{\displaystyle {\begin{aligned}\mathrm {P} (\mathbf {w} )&=\mathrm {P} {\big (}\mathbf {v} -\mathrm {P} (\mathbf {v} ){\big )}=\mathrm {P} (\mathbf {v} )-\mathrm {P} ^{2}(\mathbf {v} )\\&=\mathrm {P} (\mathbf {v} )-\mathrm {P} (\mathbf {v} )=\mathbf {0} .\end{aligned}}}
P
{\displaystyle \mathrm {P} }
v
,
{\displaystyle \mathbf {v} ,}
P
(
v
)
=
P
(
w
+
u
)
=
P
(
w
)
+
P
(
u
)
=
0
+
u
=
u
.
{\displaystyle \mathrm {P} (\mathbf {v} )=\mathrm {P} (\mathbf {w} +\mathbf {u} )=\mathrm {P} (\mathbf {w} )+\mathrm {P} (\mathbf {u} )=\mathbf {0} +\mathbf {u} =\mathbf {u} .}
↑ Niech
v
{\displaystyle \mathbf {v} }
λ
{\displaystyle \lambda }
P
.
{\displaystyle \mathrm {P} .}
λ
u
=
P
(
u
)
=
P
(
P
(
u
)
)
=
P
(
λ
u
)
=
λ
2
u
,
{\displaystyle \lambda \mathbf {u} =\mathrm {P} (\mathbf {u} )=\mathrm {P} {\big (}\mathrm {P} (\mathbf {u} ){\big )}=\mathrm {P} (\lambda \mathbf {u} )=\lambda ^{2}\mathbf {u} ,}
u
≠
0
,
{\displaystyle \mathbf {u} \neq \mathbf {0} ,}
λ
=
λ
2
,
{\displaystyle \lambda =\lambda ^{2},}
λ
(
λ
−
1
)
=
0
,
{\displaystyle \lambda (\lambda -1)=0,}
λ
=
0
{\displaystyle \lambda =0}
λ
=
1.
{\displaystyle \lambda =1.}
↑ Niech
u
1
,
…
,
u
k
{\displaystyle \mathbf {u} _{1},\dots ,\mathbf {u} _{k}}
U
.
{\displaystyle U.}
u
i
=
P
(
v
i
)
,
{\displaystyle \mathbf {u} _{i}=\mathrm {P} (\mathbf {v} _{i}),}
P
(
u
i
)
=
P
2
(
v
i
)
=
P
(
v
i
)
=
u
i
{\displaystyle \mathrm {P} (\mathbf {u} _{i})=\mathrm {P} ^{2}(\mathbf {v} _{i})=\mathrm {P} (\mathbf {v} _{i})=\mathbf {u} _{i}}
(
i
=
1
,
…
,
k
)
,
{\displaystyle (i=1,\dots ,k),}
P
{\displaystyle P}
λ
=
1.
{\displaystyle \lambda =1.}
P
{\displaystyle \mathrm {P} }
λ
=
1
{\displaystyle \lambda =1}
P
.
{\displaystyle \mathrm {P} .}
twierdzenia o rzędzie wynika jednak, że
dim
i
m
P
+
dim
ker
P
=
dim
V
1
(
P
)
+
dim
V
0
(
P
)
=
dim
V
{\displaystyle \dim \mathrm {im\;P} +\dim \ker \mathrm {P} =\dim V_{1}(\mathrm {P} )+\dim V_{0}(\mathrm {P} )=\dim V}
ker
P
=
dim
V
0
(
P
)
{\displaystyle \ker \mathrm {P} =\dim V_{0}(\mathrm {P} )}
V
.
{\displaystyle V.}
V
,
{\displaystyle V,}
V
=
i
m
P
⊕
ker
P
,
{\displaystyle V=\mathrm {im\;P} \oplus \ker \mathrm {P} ,}
P
{\displaystyle \mathrm {P} }
P
{\displaystyle \mathrm {P} }
λ
=
1
{\displaystyle \lambda =1}
P
.
{\displaystyle \mathrm {P} .}
r
a
n
k
P
=
dim
i
m
P
=
dim
V
1
(
P
)
=
t
r
P
.
{\displaystyle \mathrm {rank\;P} =\dim \mathrm {im\;P} =\dim V_{1}(\mathrm {P} )=\mathrm {tr\;P} .}
↑ Jeśli
A
=
B
D
B
−
1
,
{\displaystyle \mathrm {A} =\mathrm {BDB} ^{-1},}
D
{\displaystyle \mathrm {D} }
macierz jest macierzą diagonalną ) wyłącznie z wartościami własnymi równymi zeru lub jedynce (na przekątnej głównej), to
A
2
=
B
D
B
−
1
B
D
B
−
1
=
B
D
2
B
−
1
=
B
D
B
−
1
=
A
,
{\displaystyle \mathrm {A} ^{2}=\mathrm {BDB} ^{-1}\mathrm {BDB} ^{-1}=\mathrm {B} \mathrm {D} ^{2}\mathrm {B} ^{-1}=\mathrm {B} \mathrm {D} \mathrm {B} ^{-1}=\mathrm {A} ,}
D
2
=
D
,
{\displaystyle \mathrm {D} ^{2}=\mathrm {D} ,}
A
2
=
A
,
{\displaystyle \mathrm {A} ^{2}=\mathrm {A} ,}
A
{\displaystyle \mathrm {A} }
↑ Z bezpośredniego rachunku wynika, że
Q
2
=
(
I
−
P
)
2
=
(
I
−
P
)
(
I
−
P
)
=
I
2
−
P
I
−
I
P
+
P
2
=
I
−
2
P
+
P
=
I
−
P
=
Q
,
{\displaystyle {\begin{aligned}\mathrm {Q} ^{2}&=(\mathrm {I} -\mathrm {P} )^{2}=(\mathrm {I} -\mathrm {P} )(\mathrm {I} -\mathrm {P} )\\&=\mathrm {I} ^{2}-\mathrm {PI} -\mathrm {IP} +\mathrm {P} ^{2}\\&=\mathrm {I} -2\mathrm {P} +\mathrm {P} =\mathrm {I} -\mathrm {P} =\mathrm {Q} \end{aligned}},}
Q
2
=
Q
.
{\displaystyle \mathrm {Q} ^{2}=\mathrm {Q} .}
↑ Wychodząc od samosprzężoności i idempotentności
P
{\displaystyle \mathrm {P} }
u
,
v
∈
V
{\displaystyle \mathbf {u} ,\mathbf {v} \in V}
P
(
u
)
∈
U
,
{\displaystyle \mathrm {P} (\mathbf {u} )\in U,}
v
−
P
(
v
)
∈
W
{\displaystyle \mathbf {v} -\mathrm {P} (\mathbf {v} )\in W}
⟨
P
(
u
)
,
v
−
P
(
v
)
⟩
=
⟨
P
2
(
u
)
,
v
−
P
(
v
)
⟩
=
⟨
P
(
u
)
,
P
(
I
−
P
)
(
v
)
⟩
=
⟨
P
(
u
)
,
(
P
−
P
2
)
(
v
)
⟩
=
⟨
P
(
u
)
,
0
⟩
=
0
,
{\displaystyle {\begin{aligned}&{\big \langle }\mathrm {P} (\mathbf {u} ),\mathbf {v} -\mathrm {P} (\mathbf {v} ){\big \rangle }\\&={\big \langle }\mathrm {P} ^{2}(\mathbf {u} ),\mathbf {v} -\mathrm {P} (\mathbf {v} ){\big \rangle }\\&={\big \langle }\mathrm {P} (\mathbf {u} ),\mathrm {P} (\mathrm {I} -\mathrm {P} )(\mathbf {v} ){\big \rangle }={\big \langle }\mathrm {P} (\mathbf {u} ),(\mathrm {P} -\mathrm {P} ^{2})(\mathbf {v} ){\big \rangle }\\&={\big \langle }\mathrm {P} (\mathbf {u} ),\mathbf {0} {\big \rangle }=0\end{aligned}},}
⟨
⋅
,
⋅
⟩
{\displaystyle \langle \cdot ,\cdot \rangle }
iloczyn skalarny przestrzeni
V
,
{\displaystyle V,}
I
{\displaystyle \mathrm {I} }
operator tożsamościowy . Stąd
P
(
v
)
{\displaystyle \mathrm {P} (\mathbf {v} )}
v
−
P
(
v
)
{\displaystyle \mathbf {v} -\mathrm {P} (\mathbf {v} )}
P
{\displaystyle \mathrm {P} }
⟨
u
,
P
(
v
)
⟩
=
⟨
P
(
u
)
,
v
⟩
=
⟨
u
,
P
∗
(
v
)
⟩
{\displaystyle {\big \langle }\mathbf {u} ,\mathrm {P} (\mathbf {v} ){\big \rangle }={\big \langle }\mathrm {P} (\mathbf {u} ),\mathbf {v} {\big \rangle }={\big \langle }\mathbf {u} ,\mathrm {P} ^{*}(\mathbf {v} ){\big \rangle }}
u
,
v
∈
V
;
{\displaystyle \mathbf {u} ,\mathbf {v} \in V;}
P
=
P
∗
.
{\displaystyle \mathrm {P} =\mathrm {P} ^{*}.}
↑ Dla dowolnego wektora
v
∈
V
{\displaystyle \mathbf {v} \in V}
nierówności Cauchy’ego–Schwarza jest
‖
P
(
v
)
‖
2
=
⟨
P
(
v
)
,
P
(
v
)
⟩
=
⟨
P
(
v
)
,
v
⟩
⩽
‖
P
(
v
)
‖
‖
v
‖
,
{\displaystyle {\big \|}\mathrm {P} (\mathbf {v} ){\big \|}^{2}={\big \langle }\mathrm {P} (\mathbf {v} ),\mathrm {P} (\mathbf {v} ){\big \rangle }={\big \langle }\mathrm {P} (\mathbf {v} ),\mathbf {v} {\big \rangle }\leqslant {\big \|}\mathrm {P} (\mathbf {v} ){\big \|}\ \|\mathbf {v} \|,}
‖
P
(
v
)
‖
⩽
‖
v
‖
,
{\displaystyle {\big \|}\mathrm {P} (\mathbf {v} ){\big \|}\leqslant \|\mathbf {v} \|,}
P
{\displaystyle \mathrm {P} }
norma operatorowa
‖
P
‖
⩽
1.
{\displaystyle \|\mathrm {P} \|\leqslant 1.}
P
≠
θ
,
{\displaystyle \mathrm {P} \neq \mathrm {\theta } ,}
v
,
{\displaystyle \mathbf {v} ,}
P
(
v
)
≠
0
{\displaystyle \mathrm {P} (\mathbf {v} )\neq \mathbf {0} }
‖
P
2
(
v
)
‖
=
‖
P
(
v
)
‖
,
{\displaystyle {\big \|}\mathrm {P} ^{2}(\mathbf {v} ){\big \|}={\big \|}\mathrm {P} (\mathbf {v} ){\big \|},}
‖
P
‖
⩾
1.
{\displaystyle \|\mathrm {P} \|\geqslant 1.}
‖
P
‖
=
1.
{\displaystyle \|\mathrm {P} \|=1.}
↑ W notacji Diraca jest
P
A
=
∑
i
=
1
k
|
u
i
⟩
⟨
u
i
|
.
{\displaystyle \mathrm {P} _{\mathrm {A} }=\sum _{i=1}^{k}|\mathbf {u} _{i}\rangle \langle \mathbf {u} _{i}|.}
↑ Wtedy
P
u
(
x
)
=
u
u
∗
x
.
{\displaystyle \mathbf {P} _{\mathbf {u} }(\mathbf {x} )=\mathbf {uu} ^{*}\mathbf {x} .}
notacji Diraca jest
P
u
=
|
u
⟩
⟨
u
|
;
{\displaystyle \mathrm {P} _{\mathbf {u} }=|\mathbf {u} \rangle \langle \mathbf {u} |;}
P
u
(
x
)
=
|
u
⟩
⟨
u
|
x
⟩
.
{\displaystyle \mathrm {P} _{\mathbf {u} }(\mathbf {x} )=|\mathbf {u} \rangle \ \langle \mathbf {u} |\mathbf {x} \rangle .}
P
u
=
u
⊗
u
{\displaystyle \mathrm {P} _{\mathbf {u} }=\mathbf {u} \otimes \mathbf {u} }
iloczynu tensorowego (a dokładnie: iloczynu diadycznego ).
↑ Macierz
(
A
∗
A
)
−
1
{\displaystyle (\mathbf {A} ^{*}\mathbf {A} )^{-1}}
u
u
∗
{\displaystyle \mathbf {uu} ^{*}}
‖
u
‖
=
1
;
{\displaystyle \|\mathbf {u} \|=1;}
u
∗
u
=
‖
u
‖
2
{\displaystyle \mathbf {u} ^{*}\mathbf {u} =\|\mathbf {u} \|^{2}}
u
(
u
∗
u
)
−
1
u
∗
=
u
u
∗
/
‖
u
‖
2
{\displaystyle \mathbf {u} (\mathbf {u} ^{*}\mathbf {u} )^{-1}\mathbf {u} ^{*}=\mathbf {uu} ^{*}/\|\mathbf {u} \|^{2}}
s
p
a
n
u
.
{\displaystyle \mathrm {span\;} \mathbf {u} .}
↑ a b Oznaczenia
P
X
f
(
x
)
{\displaystyle \mathrm {P} _{X}f(x)}
(
P
X
(
f
)
)
(
x
)
,
{\displaystyle {\big (}\mathrm {P} _{X}(f){\big )}(x),}
P
X
(
f
)
{\displaystyle \mathrm {P} _{X}(f)}
L
2
(
R
)
,
{\displaystyle \mathrm {L} ^{2}(\mathbb {R} ),}
P
X
:
L
2
(
R
)
→
L
2
(
R
)
{\displaystyle \mathrm {P} _{X}\colon \mathrm {L} ^{2}(\mathbb {R} )\to \mathrm {L} ^{2}(\mathbb {R} )}
X
{\displaystyle X}
L
2
(
R
)
.
{\displaystyle \mathrm {L} ^{2}(\mathbb {R} ).}
↑ Zob. delta Kroneckera
δ
k
,
n
.
{\displaystyle \delta _{k,n}.}
↑ Por. grupa okręgu
T
.
{\displaystyle \mathbb {T} .}
F.W. Gehring, P.R. Halmos, C.C Moore: A Course in Functional Analysis . Nowy Jork: Springer-Verlag, 1985. Brak numerów stron w książce 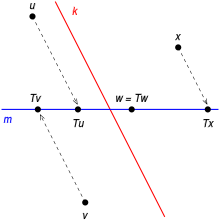























































![{\displaystyle \left[{\begin{smallmatrix}1&0\\0&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/765b8147864544b36f917d90fe67728dcd47417f)
![{\displaystyle \left[{\begin{smallmatrix}1&0\\0&0\end{smallmatrix}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef2e796a45d3fe43bc85fc38cff53215da6c0ee8)
![{\displaystyle \left[{\begin{smallmatrix}0&1\\0&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdc7bb80e487b6a387428e7d48596867cfc35b2d)































































































