Ciąg Cauchy'ego

Wykres ciągu Cauchy'ego (x_n) oznaczono niebieskim kolorem (indeks na osi odciętych, wartość na osi rzędnych). Jeżeli przestrzeń zawierająca ciąg jest zupełna, to jego granica istnieje.

Ciąg, który nie jest Cauchy'ego. Elementy ciągu nie zbliżają się do siebie wraz z jego postępem.

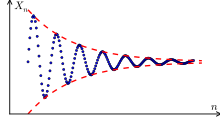
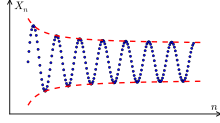
Ciąg Cauchy'ego – ciąg elementów przestrzeni metrycznej (najczęściej zbioru liczb rzeczywistych) spełniających tzw. warunek Cauchy'ego. Nazwa pojęć pochodzi od nazwiska francuskiego matematyka, Augustina Cauchy'ego.

W ogólności warunek Cauchy'ego mówi, iż kolejne elementy ciągu zbliżają się do siebie. Dokładniej, zaniedbując dostateczną (lecz nadal skończoną) liczbę elementów można ograniczyć odległości między pozostałymi elementami do odległości mniejszej niż jakakolwiek ustalona wcześniej wartość dodatnia.

Innymi słowy, wybierając ustaloną dodatnią liczbę rzeczywistą ε można, bez względu na to jak mała będzie wartość ε, wyrugować z ciągu Cauchy'ego pewną skończoną liczbę elementów, po których dowolna para pozostałych wyrazów będzie w odległości mniejszej niż ε.

Ponieważ definicja ciągu Cauchy'ego korzysta z pojęcia odległości, to pojęcie to w podanym sformułowaniu może być rozważane wyłącznie w przestrzeniach metrycznych. Uogólnia się je jednak na inne struktury matematyczne, m.in. na przestrzenie liniowo-topologiczne, przestrzenie jednostajne, czy też grupy.

Użyteczność ciągów Cauchy'ego polega przede wszystkim na tym, że w przestrzeni zupełnej (gdzie wszystkie ciągi tego typu są zbieżne), dają one użyteczne kryterium zbieżności zależne wyłącznie od wyrazów tego ciągu. Fakt ten wykorzystuje się często w algorytmach, zarówno teoretycznych jak i stosowanych, gdzie można łatwo wykazać zbieżność procesu iteracji poprzez wskazanie ciągu Cauchy'ego złożonego z poszczególnych iteracji.

Powyższe intuicje nie są tak obce, jak mogłyby wydawać się na pierwszy rzut oka. Przystanie na fakt, że każda liczba rzeczywista ma rozwinięcie dziesiętne, jest przyznaniem, że pewien ciąg Cauchy'ego liczb wymiernych (którego wyrazy są kolejnymi obcięciami rozszerzenia dziesiętnego) ma granicę będącą określoną liczbą rzeczywistą – zob. ciąg podstawowy. Na podobnej zasadzie ciągi Cauchy'ego posłużyły Georgowi Cantorowi do formalnej konstrukcji zbioru liczb rzeczywistych.

Warunek Cauchy'ego

Liczby rzeczywiste

Niech $(a_i)_{i \in \mathbb N}$ będzie ciągiem liczbowym. Spełnia on warunek Cauchy'ego wtedy i tylko wtedy, gdy

$\forall_{\varepsilon \in \mathbb Q, \varepsilon > 0}\; \exists_{N \in \mathbb N}\; \forall_{m, n > N}\; |a_m - a_n| < \varepsilon.$

Przestrzenie metryczne

Niech (X,d) będzie przestrzenią metryczną i niech $(a_i)_{i \in \mathbb N}$ będzie ciągiem elementów tej przestrzeni. Spełnia on warunek Cauchy'ego wtedy i tylko wtedy, gdy

$\forall_{\varepsilon > 0}\; \exists_{N \in \mathbb N}\; \forall_{m, n > N}\; d(a_m, a_n) < \varepsilon.$

Definicję ciągu Cauchy'ego można wyrazić również za pomocą średnicy zbioru: jeżeli $A_k = \{a_k, a_{k+1}, a_{k+2}, \dots\}$, to (a_i) jest ciągiem Cauchy'ego, gdy

$\lim_{k \to \infty}\; \operatorname{diam}\; A_k = 0.$

Własności

W dowolnej przestrzeni metrycznej prawdziwe są zdania:

• każdy ciąg zbieżny spełnia warunek Cauchy'ego,
• każdy ciąg Cauchy'ego jest ograniczony,
• ciąg Cauchy'ego zawierający podciąg zbieżny do pewnej liczby g jest zbieżny do g.

W przestrzeniach euklidesowych $\mathbb R^k$ (w szczególności dla liczb rzeczywistych) dodatkowo zachodzą własności:

• ciąg punktów $\mathbf x_n = (x_{n, 1}, \dots, x_{n, k})$ jest ciągiem Cauchy'ego wtedy i tylko wtedy, gdy każdy z ciągów $x_{n, 1}, \dots, x_{n, k}$ jest ciągiem Cauchy'ego;
• ciąg jest zbieżny wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego.

Przykłady

• Ciąg liczbowy o wyrazie ogólnym $a_n = \tfrac{1}{n}$ jest ciągiem Cauchy'ego, gdyż

  $\left|\tfrac{1}{p} - \tfrac{1}{q}\right| \leqslant \tfrac{1}{p} + \tfrac{1}{q} \leqslant \tfrac{2}{q}$ dla $q \leqslant p.$ Wystarczy dla ustalonego ε > 0 przyjąć $n_0 > \tfrac{2}{\varepsilon}.$

• Ciąg liczbowy o wyrazie ogólnym a_n = n nie jest ciągiem Cauchy'ego, bo $|a_p - a_q| = |p - q| \geqslant 1$ dla $p \neq q$ ciąg ten jest nieograniczony, a na mocy drugiej własności ciąg Cauchy'ego jest ograniczony.

Ciąg podstawowy

Ciągiem podstawowym nazywa się ciąg Cauchy'ego liczb wymiernych. Ich głównym zastosowaniem jest konstrukcja liczb rzeczywistych w oparciu o liczby wymierne.

Ciągi liczb wymiernych stały, czy zbieżny do liczby wymiernej są podstawowe, np. podstawowy jest ciąg $\left(\tfrac{3n + 1}{n + 2}\right)$ i ma on granicę równą 3.

Podstawowe są również ciągi monotonicznie rosnące (malejące) i ograniczone z góry (z dołu). W ogólności każdy ciąg podstawowy jest ograniczony.

Ciąg przybliżeń dziesiętnych dowolnej liczby rzeczywistej również jest ciągiem podstawowym. Na przykład ciąg

$(\pi_n) = (3;\ 3{,}1;\ 3{,}14;\ 3{,}141;\ 3{,}1415;\ 3{,}14159;\ \dots)$

kolejnych przybliżeń liczby π (zob. pi) jest podstawowy. Ciąg ten nie ma granicy wymiernej, jest więc rozbieżny w przestrzeni liczb wymiernych.

Zbiór ciągów podstawowych jest zamknięty ze względu na sumy (różnice), iloczyny oraz ilorazy, o ile tylko są one dobrze określone.

Zupełność

• Przestrzeń metryczną, w której każdy ciąg Cauchy'ego jest zbieżny nazywa się przestrzenią zupełną.
• Przestrzeń unormowaną, która jest zupełna (w sensie metryki generowanej przez normę), nazywa się przestrzenią Banacha.
• Przestrzeń unitarną zupełną nazywa się przestrzenią Hilberta.

W szczególności przestrzeń $\mathbb R$ (z wartością bezwzględną) i przestrzeń $\mathbb R^k$ (z metryką euklidesową) są zupełne.

Inne postaci

Szeregi

Ponieważ szeregi z definicji są ciągami sum częściowych, można rozważać warunek Cauchy'ego również dla nich.

Niech $(E, \|\cdot\|)$ będzie przestrzenią Banacha, a $(a_n)_{n \in \mathbb N}$ ciągiem jej elementów. Szereg $\sum~a_i$ spełnia warunek Cauchy'ego, jeżeli

$\forall_{\varepsilon > 0}\; \exists_{N \in \mathbb N}\; \forall_{m > n > N}\; \left\|\sum_{i = n + 1}^m~a_i\right\| < \varepsilon.$

Szereg $\sum~a_i$ jest zbieżny wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego. W szczególności powyższa definicja obowiązuje dla $\bigl(\mathbb R^k, |\cdot|\bigr).$

Przestrzenie liniowo-topologiczne

W przestrzeniach liniowo-topologicznych ciąg Cauchy'ego można zdefiniować w naturalny sposób bez uciekania się do pojęcia metryki.

Ciąg $(x_n)_{n \in \mathbb N}$ punktów przestrzeni liniowo-topologicznej X nazywa się ciągiem Cauchy'ego wtedy i tylko wtedy, gdy dla każdego otoczenia zera $U\subseteq X,$ istnieje taka liczba naturalna N, że dla m,n > N jest

$\mathbf x_n - \mathbf x_m \in U.$

W przestrzeni liniowo-topologicznej spełnione są własności obowiązujące w przestrzeniach metrycznych. Jeżeli topologia przestrzeni X jest wyznaczona przez niezmienniczą na przesunięcia metrykę d, to ciąg elementów tej przestrzeni jest ciągiem Cauchy'ego wtedy i tylko wtedy, gdy spełnia warunek Cauchy'ego względem tej metryki.

W szczególności, przestrzeń liniowo-topologiczna jest przestrzenią Frécheta wtedy i tylko wtedy, gdy ma ona przeliczalną bazę lokalną i każdy ciąg Cauchy'ego punktów tej przestrzeni jest zbieżny.

Zobacz też

• twierdzenie Baire'a

Bibliografia

• Kołodziej, Witold. Analiza matematyczna. Warszawa : PWN, 1979.
• Leja, Franciszek. Rachunek różniczkowy i całkowy. Warszawa : PWN, 1976.
• Maurin, Krzysztof. Analiza – Część I – Elementy. Warszawa : PWN, 1976.
• Musielakowie, Helena i Julian. Analiza matematyczna. Poznań : Wydawnictwo Naukowe UAM, 2000.
• Walter Rudin: Analiza Funkcjonalna. Warszawa: PWN, 2001.