Funkcja wzajemnie jednoznaczna

Funkcja wzajemnie jednoznaczna, bijekcja – wzajemnie jednoznaczna odpowiedniość między elementami dwóch zbiorów, czyli funkcja będąca jednocześnie iniekcją i suriekcją (funkcją różnowartościową i funkcją „na”). Równoważnie:
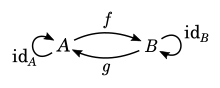
- funkcja jest bijekcją wtedy i tylko wtedy, gdy istnieje funkcja do niej odwrotna[1] – również i ona jest bijekcją;
- przy bijekcji przeciwobraz każdego singletonu również jest singletonem[potrzebny przypis].
Bijekcje pozwalają zdefiniować rozmaite relacje równoważności między obiektami, m.in.:
- równoliczności zbiorów w kombinatoryce i teorii mnogościi,
- izomorfizmu struktur w algebrze abstrakcyjnej i teorii kategorii;
- homeomorfizmu, izometrii i dyfeomorfizmu przestrzeni w topologii.
Duże znaczenie odgrywają też bijekcje endofunkcyjne, tj. przekształcające zbiór w siebie (f:X→X). Bywają nazywane permutacjami – zwłaszcza dla zbiorów skończonych – i tworzą struktury znane jako grupy symetryczne; przekształcenia te pozwalają zdefiniować symetrię figur i innych obiektów. Bijekcje zbioru w siebie po nałożeniu dodatkowych warunków tworzą podgrupy grup symetrycznych, np. grupy alternujące, grupy automorfizmów, izometrii czy dyfeomorfizmów. Szczególnym rodzajem endobijekcji są też inwolucje i inne funkcje torsyjne (skończonego rzędu).
Termin bijekcja powstał najpóźniej w 1954 roku, kiedy pojawił się w pracy zespołu Nicolas Bourbaki[2].
Przykłady[edytuj | edytuj kod]
- Alfabet – ciąg liter danej ortografii, zawierający wszystkie z nich (suriektywność) i każdą dokładnie raz (iniektywność);
- listy obecności – ciągi wszystkich osób z ustalonego zbioru;
- zmiana systemu liczbowego – np. z dziesiętnego na rzymski lub binarny – to bijekcja między zbiorami napisów przedstawiających liczby;
- logarytm w dziedzinie rzeczywistej;
- dowolna iniekcja z przeciwdziedziną zawężoną do obrazu tej funkcji.
Bijekcje działające wewnątrz ustalonego zbioru:
- dowolna niestała funkcja liniowa (funkcja stopnia pierwszego) zmiennej rzeczywistej; tworzą one grupę afiniczną prostej rzeczywistej;
- niektóre inne wielomiany rzeczywiste stopnia nieparzystego, np. x3;
- homografie zmiennej rzeczywistej, również tworzące grupę;
- niektóre pierwiastniki, np. (x−1)1/3;
- sinus i tangens hiperboliczny.
Przykłady zawiera też artykuł o inwolucjach.
Grupa bijekcji[edytuj | edytuj kod]
Rozważając zbiór wszystkich bijekcji ustalonego zbioru można przekonać się o tym, że:
- składanie funkcji jest działaniem dwuargumentowym w tym zbiorze,
- działanie to jest łączne,
- funkcja tożsamościowa jest elementem neutralnym tego działania,
- każda bijekcja ma jednoznacznie określoną do niej bijekcję odwrotną.
W ten sposób zbiór bijekcji z działaniem ich składania spełnia aksjomaty grupy i nazywa się grupą bijekcji.
Tego rodzaju grupy były historycznie jednymi z pierwszych rozważanych grup. Okazuje się, że grupy bijekcji są modelem wszystkich możliwych grup abstrakcyjnych, tj. dowolną grupę można przedstawić w postaci pewnej grupy bijekcji (twierdzenie Cayleya).
Zobacz też[edytuj | edytuj kod]
- Twierdzenie Cantora-Bernsteina-Schrödera – warunek równoważny na istnienie bijekcji.
Przypisy[edytuj | edytuj kod]
- ↑ bijekcja, [w:] Encyklopedia PWN [dostęp 2022-12-16].
- ↑
 Jeff Miller, Injection, surjection and bijection [w:] Earliest Known Uses of Some of the Words of Mathematics (I) (ang.), MacTutor History of Mathematics archive, University of St Andrews, mathshistory.st-andrews.ac.uk [dostęp 2022-12-16].
Jeff Miller, Injection, surjection and bijection [w:] Earliest Known Uses of Some of the Words of Mathematics (I) (ang.), MacTutor History of Mathematics archive, University of St Andrews, mathshistory.st-andrews.ac.uk [dostęp 2022-12-16].

