Pochodna

Pochodna – w analizie matematycznej miara szybkości zmian wartości funkcji względem zmian jej argumentów.

Pochodna funkcji zmiennej rzeczywistej o wartościach rzeczywistych

Niech $y = f(x)\;$ będzie funkcją rzeczywistą zmiennej rzeczywistej $x$ określoną w otoczeniu punktu $x_0$. Pochodną funkcji f(x) w punkcie $x_0$ nazywamy granicę (o ile istnieje):

$\lim_{\Delta x \to 0}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$

Co symbolicznie zapisuje się w jednej z postaci:

$\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \frac{d y}{d x} = \frac{d}{d x} f(x_0) = f'(x_0) = y'(x_0)$,

We wzorze tym:

• $\Delta x\;$ jest przyrostem zmiennej niezależnej x,
• $\Delta y = f(x_0 + \Delta x) - f(x_0)\;$ jest przyrostem zmiennej zależnej y,
• Wyrażenie $\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = \frac{\Delta y}{\Delta x}$ nazywa się ilorazem różnicowym; jest on funkcją przyrostu zmiennej niezależnej.

Jeżeli przyjmie się, że $x = x_0 + \Delta x$, to pochodną w punkcie $x_0$ można zapisać następująco:

$\lim_{x \to x_0}~\frac{f(x) - f(x_0)}{x - x_0}$.

Często w publikacjach przyrost $\Delta x$ oznacza się literą h. Wtedy pochodna jest równa:

$\lim_{h \to 0}~\frac{f(x_0 + h) - f(x_0)}{h}$.

Jeśli funkcja $\scriptstyle f$ ma pochodną dla każdego elementu swej dziedziny $\scriptstyle U,$ to można rozważać odwzorowanie przypisujące każdemu argumentowi, jego pochodną dla tego elementu. Przekształcenie to nazywa się funkcją pochodną funkcji $\scriptstyle f$ lub krótko: pochodną $\scriptstyle f;$ w dalszej części artykułu będzie ono oznaczane symbolem $\scriptstyle f'$ – pozostałe oznaczenia opisano w oddzielnej sekcji – w ten sposób $\scriptstyle f'(x)$ oznaczać będzie pochodną funkcji $\scriptstyle f$ dla argumentu $\scriptstyle x;$ w tym wypadku $\scriptstyle f'$ również jest funkcją zmiennej rzeczywistej o wartościach rzeczywistych.

Własności funkcji pochodnej

• iloczyn pochodnej przez stałą,

$(af)'(x) = af'(x)\;$

• pochodną sumy funkcji (addytywność),

$(f + g)'(x) = f'(x) + g'(x)\;$;

• pochodną iloczynu funkcji (reguła Leibniza),

$(fg)'(x) = f'(x) g(x) + f(x) g'(x)\;$

• pochodną złożenia funkcji (reguła łańcuchowa),

$f'(x) = h'\bigl(g(x)\bigr) g'(x) \quad\text{ dla }\quad f(x) = h(g(x)).$

• pochodną funkcji odwrotnej,

$\left(f^{-1}\right)'(y) = \bigl(f'(x)\bigr)^{-1}, \quad\text{ o ile }\quad f'(x) \ne 0.$

• pochodną odwrotności funkcji (reguła odwrotności),

$\left(\tfrac{1}{g(x)}\right)' = \frac{-g'(x)}{g^2(x)}, \quad\text{ o ile }\quad g(x) \ne 0$

• pochodną ilorazu funkcji (reguła ilorazu),

$\left(\tfrac{f(x)}{g(x)}\right)' = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}, \quad\text{ o ile }\quad g(x) \ne 0$.

Przykłady

Istnieje pewien zestaw funkcji uważanych za elementarne, które wykorzystuje się do obliczania pochodnych bardziej skomplikowanych funkcji i ich złożeń; niech $\scriptstyle a$ oznacza stałą, zaś $\scriptstyle n$ będzie liczbą naturalną, wówczas:

• funkcje stałe i funkcje potęgowe,

  $(a)' = 0, \qquad\qquad (x^n)' = nx^{n-1};$

• funkcje wykładnicze i logarytmiczne

  $\begin{matrix} \left(e^x\right)' = e^x, & \qquad (a^x)' = a^x \ln a; \\ (\ln x)' = \frac{1}{x}, & \qquad (\log_a x)' = \frac{1}{x \ln a}; \end{matrix}$

• funkcje trygonometryczne,

  $(\sin x)' = \cos x, \qquad (\cos x)' = -\sin x;$

  $(\mathrm{tg}\; x)' = \sec^2 x = \tfrac{1}{\cos^2 x} = 1 + \mathrm{tg}^2\; x.$

• funkcje cyklometryczne,

  $(\arcsin x)' = \tfrac{1}{\sqrt{1 - x^2}};$

  $(\arccos x)' = -\tfrac{1}{\sqrt{1 - x^2}};$

  $(\mathrm{arctg}\; x)' = \tfrac{1}{{1 + x^2}};$

  $(\mathrm{arcctg}\; x)' = -\tfrac{1}{{1 + x^2}};$

wszędzie, gdzie powyższe wzory mają sens.

Pochodne wyższego rzędu

Jeżeli pochodna funkcji $f: (a, b) \to \mathbb{R}$ i stnieje w każdym punkcie przedziału otwartego (a, b), to otrzymujemy funkcję $f': (a, b) \to \mathbb{R}$, taką że

$x \mapsto f'(x)$ dla x ∈ (a, b).

Funkcję tę nazywamy pierwszą pochodną funkcji f. Ta funkcja może być również różniczkowalna w każdym punkcie przedziału (a, b). Różniczkując ją, otrzymujemy drugą pochodną funkcji f:

$x \mapsto f''(x)$ dla x ∈ (a, b).

Oznaczamy to następująco:

$f''(x) = f^{(2)}(x) = (f'(x))'\;$ lub $y'' = (y')'\;$.

Ogólnie pochodną rzędu n określamy rekurencyjnie:

$f^{(n)}(x) = (f^{(n - 1)}(x))'\;$ lub $y^{(n)} = (y^{(n - 1)})'\;$.

Przykłady

1. $(e^x)^{(n)} = e^x\;$
2. $(x^m)' = m x^{m - 1}, (x^m)'' = m (m - 1) x^{m - 2}, \cdots (x^m)^{(n)} = m (m - 1) \cdots (m - n + 1) x^{m - n}$
3. $(x^m)^{(m)} = m!, (x^m )^{(m + 1)} = 0\;$
4. $(a^x)^{(n)} = a^x \ln^{n} a\;$
5. $(\sin x)^{(n)} = \sin (x + \frac{\pi n}{2}), (\cos x)^{(n)} = \cos (x + \frac{\pi n}{2})$
6. n-tą pochodną iloczynu funkcji można wyrazić za pomocą pochodnych czynników oraz współczynników Newtona wzorem:

$(uv)^{(n)} = \sum_{k = 0}^{n} C_{n}^{k} u^{n - k} v^{k}$

Zastosowania w fizyce

Prędkość chwilowa

Jeśli funkcja $s = f (t)$ wyraża ruch punktu na prostej, którą rozpatruje się jako oś współrzędnych s, to s jest współrzędną poruszającego się punktu w chwili t. Droga, którą przebędzie punkt w przedziale czasu [t, t + Δt] jest równa

$\Delta s = f(t + \Delta t) - f(t)\;$

Prędkością średnią na tym odcinku jest wielkość:

$v_{sr} = \frac{\Delta s}{\Delta t} = \frac{f(t + \Delta t) - f(t)}{\Delta t}$.

Prędkość chwilowa w momencie t jest równa:

$v = \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t} = f'(t)$

Natężenie prądu

Prąd elektryczny polega na przepływie ładunków elektrycznych przez przewodnik. Przez Q(t) oznacza się ładunek przepływający przez ustalony przekrój przewodnika w chwili t. Wtedy w czasie Δt przez ten przekrój przepływa ładunek elektryczny $\Delta Q = Q (t + \Delta t) - Q (t)$ jest ładunkiem elektrycznym przepływającym przez ten przekrój, a wielkość

$I_{sr} = \frac{\Delta Q}{\Delta t} = \frac{Q (t + \Delta t) - Q (t)}{\Delta t}$

nazywa się średnim natężeniem prądu.

Chwilowym natężeniem prądu jest wielkość:

$I = \frac{dQ}{dt}(t) = \lim_{\Delta t \to 0} \frac{\Delta Q}{\Delta t}$

Gęstość rozkładu masy

Jeśli na przedziale [a, b] osi x dany jest pewien rozkład masy, taki że łączna masa przedziału [a, x] jest równa M (x) dla a ≤ x ≤ b. Masa znajdująca się na przedziale [x, x + Δ x] jest równa:

$\Delta M = M (x + \Delta x) - M(x)\;$.

Średnia gęstość masy na tym przedziale jest równa:

$\frac{\Delta M}{\Delta x}$,

a granica

$\lim_{\Delta x \to 0} \frac{\Delta M}{\Delta x} = M'(x) = \mu (x)$

jest gęstością rozkładu masy w punkcie x.

Pojęcie gęstości rozkładu masy jest bardzo intensywnie używane w rachunku prawdopodobieństwa i statystyce. Całkowita "masa" prostej jest wtedy równa 1 i mówi się o gęstości rozkładu prawdopodobieństwa.

Geometryczny sens pochodnej

Styczna do wykresu funkcji

• Proste, które mają lokalnie jeden punkt wspólny z krzywą
• 

  Prosta nieprzecinająca krzywej w jednym punkcie, ale będąca styczną.

• 

  Prosta przecinająca krzywą w jednym punkcie będąca styczną.

• 

  Prosta przecinająca krzywą w jednym punkcie niebędąca styczną.

Elementarna definicja stycznej do okręgu jako prostej mającej dokładnie jeden (tzn. jeden i tylko jeden) punkt z nim wspólny nie jest wystarczający dla innych krzywych (patrz rysunki powyżej).

Styczna w punkcie $\scriptstyle P$ jako granica siecznych $\scriptstyle PQ.$

Styczna i sieczna do krzywej Γ.

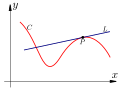
W matematyce styczną do krzywej w punkcie P (patrz rysunek obok) jest prosta, będąca granicą siecznych do krzywej przechodzących przez punkty P i Q, gdy Q dąży do P. Granica ta nie zawsze istnieje, ale jej istnienie związane jest z istnieniem pochodnej funkcji wyznaczającej tę krzywą.

Niech będzie dana funkcja ciągła y = f(x) na przedziale otwartym (a, b). Jej wykres Γ (kolor czerwony na rysunku) jest nazywany krzywą ciągłą. Współczynnik kierunkowy siecznej (kolor niebieski na rysunku) przechodzącej przez punkty A = (x, f(x)) i B = (x + Δx, f(x + Δx)) należące do przedziału (a, b) jest równy (patrz rysunek obok):

$\operatorname{tg} \beta = \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) - f(x)}{\Delta x}$.

Wtedy współczynnik kierunkowy stycznej w punkcie A (kolor zielony na rysunku) jest równy:

$\operatorname{tg} \alpha = \lim_{\beta \to \alpha} \operatorname{tg} \beta = \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = f'(x)$.

Różniczka funkcji

Zaznaczona niebieskim kolorem styczna do funkcji $\scriptstyle f$ dla argumentu $\scriptstyle x,$ tj. w punkcie $\scriptstyle P = (x, f(x))$ wraz z zaznaczonymi różniczkami.

Funkcja $f: (a, b) \to \mathbb{R}$ ma pochodną skończoną wtedy i tylko wtedy, gdy istnieje taka liczba A, że:

$\Delta y = A \cdot \Delta x + o_{\Delta x \to 0}(\Delta x)$,

gdzie A jest zależna od x, ale niezależna od Δx. Funkcja $o_{\Delta x \to 0}(\Delta x)$ zgodnie z notacją małego "o" ma własność:

$\lim_{\Delta x \to 0}\frac{o_{\Delta x \to 0}(\Delta x)}{\Delta x} = 0$.

Stąd wynika, że pochodna jest współczynnikiem liniowym prostej najlepiej aproksymującej funkcję w otoczeniu punktu x (jest to styczna do wykresu funkcji w x):

$\Delta y \approx f'(x) \cdot \Delta x\;$.

Wyrażenie po prawej stronie nazywa się często głównym członem przyrostu Δy lub różniczką funkcji f i oznacza się je symbolem dy = df:

$dy = df = f'(x) \Delta x\;$.

Przyrost zmiennej niezależnej Δx nazywa się wtedy różniczką zmiennej x:

$\Delta x = dx\;$

i różniczkę dowolnej funkcji f zazwyczaj zapisujemy tak:

$dy = f'(x) dx\;$,

skąd wynika, że pochodna funkcji f w punkcie x jest równa stosunkowi różniczki funkcji f w tym punkcie do różniczki zmiennej niezależnej x:

$f'(x) = \frac{dy}{dx}$.

Jednym z zastosowań różniczek w praktyce jest możliwość zastąpienia różnic łatwiejszymi do obliczania różniczkami. Na przykład

$|\Delta y| \approx |dy|$ dla błędu bezwzględnego przybliżenia oraz

$\Big|\frac{\Delta y}{y}\Big| \approx \Big|\frac{dy}{y}\Big|$ dla błędu względnego przybliżenia.

Przykład zastosowania różniczek

Jeśli

$\sqrt[3]{27,005} \approx \sqrt[3]{27} = 3$

to błąd jest w przybliżeniu równy różniczce funkcji y = x^1/3 w punkcie x = 27, odpowiadającego przyrostowi Δx = 0,005:

$dy = \frac{1}{3} x^{-2/3} \Delta x = \frac{1}{3} 27^{-2/3} \cdot 0,005 = \frac{1}{5400} \approx 0,0002$.

Badanie zmienności funkcji

Pochodna a monotoniczność funkcji, ekstrema i punkty przegięcia

Z twierdzenia Lagrange'a wynikają następujące własności pochodnej:

Jeżeli funkcja $f: (a, b) \to \mathbb{R}$ jest różniczkowalna, to

1. Jeśli $\forall_{x \in (a, b)} f'(x) > 0$, to f jest funkcją rosnącą na (a, b).
2. Jeśli $\forall_{x \in (a, b)} f'(x) \geqslant 0$, to f jest funkcją niemalejącą na (a, b).
3. Jeśli $\forall_{x \in (a, b)} f'(x) < 0$, to f jest funkcją malejącą na (a, b).
4. Jeśli $\forall_{x \in (a, b)} f'(x) \leqslant 0$, to f jest funkcją nierosnącą na (a, b).
5. Jeśli $\forall_{x \in (a, b)} f'(x) = 0$, to f jest funkcją stałą na (a, b).

Z własności tych wynika, że ważnymi punktami dziedziny funkcji różniczkowalnej są miejsca zerowe jej pochodnej. Ponieważ funkcja różniczkowalna jest funkcją ciągłą, więc jeśli funkcja jest określona na przedziale otwartym, to zbiory rozwiązań nierówności $f' > 0\;$ i $f' < 0\;$ są sumami przedziałów otwartych.

Zbiór miejsc zerowych pochodnej jest zbiorem domkniętym. Miejsca zerowe pierwszej pochodnej są bardzo ważne w badaniu funkcji. W praktyce obliczeniowej funkcje na ogół mają skończoną lub przeliczalną liczbę miejsc zerowych, które dzielą dziedzinę na przedziały otwarte, w których pochodna jest stale dodatnia lub stale ujemna. Wtedy każde miejsce zerowe albo oddziela dwa przedziały, na których pochodna przyjmuje jednakowe znaki, albo różne znaki. Stąd wynikają następujące definicje.

• Funkcja $f: (a, b) \to \mathbb{R}$ przyjmuje w punkcie x₀ maksimum, jeśli istnieje takie otoczenie tego punktu $(x_0 - \delta, x_0 + \delta) \subset (a, b)$, że dla każdego $x \in (x_0 - \delta, x_0) \cup (x_0, x_0 + \delta)$ zachodzi nierówność $f (x) < f (x_0)\;$.

Dla funkcji różniczkowalnej oznacza to, że jeśli pochodna funkcji f jest:

dodatnia w przedziale $(x_0 - \delta, x_0)$,

równa zero w x₀,

ujemna w przedziale $(x_0, x_0 + \delta)$

to funkcja f ma w x₀ maksimum.

• Funkcja $f: (a, b) \to \mathbb{R}$ przyjmuje w punkcie x₀ minimum, jeśli istnieje takie otoczenie tego punktu $(x_0 - \delta, x_0 + \delta) \subset (a, b)$, że dla każdego $x \in (x_0 - \delta, x_0) \cup (x_0, x_0 + \delta)$ zachodzi nierówność $f (x) > f (x_0)\;$.

Dla funkcji różniczkowalnej oznacza to, że jeśli pochodna funkcji f jest:

ujemna w przedziale $(x_0 - \delta, x_0)$,

równa zero w x₀,

dodatnia w przedziale $(x_0, x_0 + \delta)$

to funkcja f ma w x₀ minimum.

Minima i maksima funkcji nazywamy jej ekstremami.

• Funkcja $f: (a, b) \to \mathbb{R}$ ma w punkcie x₀ punkt przegięcia, jeśli jej pochodna jest:

równa zero w x₀,

albo dodatnia, albo ujemna w zbiorze $(x_0 - \delta, x_0) \cup (x_0, x_0 + \delta)$.

Schemat badania zmienności funkcji

Przed narysowaniem wykresu funkcji $f: (a, b) \to \mathbb{R}$ należy:

1. Znaleźć dziedzinę funkcji. Znaleźć granice funkcji w punktach brzegu dziedziny.
2. Znaleźć miejsca zerowe pochodnej funkcji, punkty, w których pochodna funkcji nie istnieje lub jest równa ±∞. Obliczyć wartości funkcji w tych punktach i stwierdzić, czy w tych punktach funkcja przyjmuje minimum lub maksimum.
3. Na każdym z przedziałów wyznaczonych przez miejsca zerowe pochodnej ustalić, czy funkcja jest rosnąca, czy malejąca.
4. Zbadać istnienie punktów przegięcia funkcji.
5. Rozwiązać, jeśli to możliwe, równanie $f (x) = 0$ oraz ustalić przedziały, w których funkcja ma stały znak.
6. Znaleźć asymptoty funkcji.

Funkcje wielu zmiennych

Pochodne cząstkowe

W przypadku funkcji wielu zmiennych $\scriptstyle f\colon \mathbb R^n \to \mathbb R$ możliwe jest ustalenie $\scriptstyle n-1$ jej argumentów i traktowanie jej jako funkcji jednej zmiennej – pochodną względem tej zmiennej nazywa się „pochodną cząstkową”. Jeśli $\scriptstyle \mathrm x \mapsto f(\mathrm x),$ gdzie $\scriptstyle \mathrm x = (x_1, \dots, x_n),$ to pochodną cząstkową funkcji $\scriptstyle f$ względem jej $\scriptstyle i$-tej współrzędnej $\scriptstyle x_i$ nazywa się wartość granicy

$\lim_{h \to 0} \frac{f(x_1, \dots, x_{i-1}, x_i + h, x_{i+1}, \dots, x_n) - f(x_1, \dots, x_n)}{h},$

o ile istnieje i jest skończona. W zapisie wektorowym powyższą granicę można zapisać wzorem

$\lim_{h \to 0} \frac{f(\mathrm x + \mathbf h) - f(\mathrm x)}{h},$

gdzie $\scriptstyle \mathbf h = (0, \dots, 0, h, 0, \dots, 0)$ jest wektorem o jedynej niezerowej współrzędnej $\scriptstyle i$-tej.

Powyższą definicję można rozszerzyć zauważając, że $\scriptstyle \mathbf h = h\mathbf e_i,$ gdzie $\scriptstyle \mathbf e_i$ jest wektorem bazy standardowej przestrzeni $\scriptstyle \mathbb R^n.$ Wybranie dowolnego wektora jednostkowego $\scriptstyle \mathbf u$ zamiast wektora bazy prowadzi do definicji pochodnej kierunkowej wzdłuż $\scriptstyle \mathbf u,$ mianowicie:

$\lim_{h \to 0} \frac{f(\mathrm x + h\mathbf u) - f(\mathrm x)}{h}.$

Jeśli $\scriptstyle \mathbf u = u_1 \mathbf e_1 + \dots + u_n \mathbf e_n$ jest wektorem jednostkowym, to pochodna kierunkowa funkcji $\scriptstyle f$ wzdłuż $\scriptstyle u$ jest równa kombinacji liniowej pochodnych cząstkowych funkcji $\scriptstyle f$ o współczynnikach $\scriptstyle u_1, \dots, u_n.$

Pochodne zupełne

W czerwonym punkcie paraboloidy funkcja $\scriptstyle \mathbb R^2 \to \mathbb R$ ją opisująca przyjmuje maksimum: warunkiem koniecznym jego istnienia jest znikanie pochodnej (w słabym/silnym sensie) wspomnianej funkcji.

Dowolną funkcję $\scriptstyle \mathrm f\colon \mathbb R^n \to \mathbb R^m$ można rozłożyć na funkcje współrzędnych $\scriptstyle f_1, \dots, f_m\colon \mathbb R^n \to \mathbb R$ przyjmując $\scriptstyle \mathrm f = (f_1, \dots, f_m).$ Jeżeli funkcje te są różniczkowalne w każdym kierunku, co jest równoważne istnieniu ich wszystkich pochodnych cząstkowych, to funkcję $\scriptstyle \mathrm f$ nazywa się różniczkowalną w słabym sensie; przedstawieniem tej pochodnej we współrzędnych za pomocą odpowiadającej jej macierzy przekształcenia liniowego jest tzw. macierz Jacobiego.

Mogłoby się wydawać, że definicja słabej pochodnej jest w zupełności zadowalająca, jednak w przypadku funkcji wielowymiarowych należy zwrócić uwagę na zjawiska związane z większą liczbą wymiarów: istnieją przykładowo funkcje, które mają pochodne we wszystkich kierunkach (równoważnie: mają wszystkie pochodne cząstkowe, zob. ostatni ustęp poprzedniej sekcji), czyli wzdłuż prostych, lecz nie mają pochodnych wzdłuż innych krzywych – problem ten nie istnieje w przypadku funkcji zmiennej rzeczywistej, gdzie granicę można obliczać wyłącznie wzdłuż krzywych leżących wyłącznie na prostej.

Definicja pochodnej funkcji wielu zmiennych $\scriptstyle \mathrm f$ stanowiącą rozwiązanie tego problemu naśladuje definicję „różniczkową” dla funkcji rzeczywistej (zob. Związek z różniczką). Pochodną w mocnym sensie funkcji $\scriptstyle \mathrm f$ dla argumentu punktowego $\scriptstyle \mathrm x \in \mathbb R^n$ nazywa się takie przekształcenie liniowe $\scriptstyle \mathrm{A_x}\colon \mathbb R^n \to \mathbb R^m,$ dla którego zachodzi

$\lim_{|\mathbf h| \to 0}~\frac{\bigl|\mathrm f(\mathrm x + \mathbf h) - \mathrm f(\mathrm x) - \mathrm{A_x}(\mathbf h)\bigr|}{|\mathbf h|} = 0,$

gdzie $\scriptstyle |\cdot|$ oznacza moduł odpowiednich wektorów; odwzorowanie $\scriptstyle \mathbf h \mapsto \mathrm{A_x}(\mathbf h),$ podobnie jak w przypadku jednowymiarowym, nazywa się różniczką (w mocnym sensie) funkcji $\scriptstyle \mathrm f$. Rolę funkcji pochodnej pełni tu więc odwzorowanie $\scriptstyle \mathrm A\colon \mathbb R^n \to \mathrm L(\mathbb R^n, \mathbb R^m)$ przestrzeni współrzędnych w przestrzeń liniową przekształceń liniowych (por. przestrzeń funkcyjna przekształceń liniowych) dane wzorem $\scriptstyle \mathrm x \mapsto \mathrm{A_x},$ tj. przypisujące punktowi przekształcenie liniowe.

Istnienie pochodnej w silnym sensie pochodnej pociąga istnienie pochodnej w słabym sensie; jeżeli jednak funkcja jest różniczkowalna w słabym sensie i wszystkie jej pochodne cząstkowe (kierunkowe) są ciągłe, to funkcja jest różniczkowalna w silnym sensie w sposób ciągły (tzn. jest klasy $\scriptstyle \mathrm C^1$). Oba rodzaje pochodnych mają wiele własności pochodnej funkcji rzeczywistej, np. liniowość, czy zachodzenie reguły łańcuchowej. Bezpośrednie generalizacje pojęć pochodnych w słabym/silnym sensie, tj. pochodne Gâteaux/Frécheta, opisano w Uogólnieniach.

Oznaczenia

Przez długie lata Leibniz wiódł spór z Newtonem o pierwszeństwo odkrycia rachunku różniczkowego.

Prace Lagrange'a miały wielki wpływ na Cauchy'ego, Jacobiego i Weierstrassa uważanych za twórców współczesnej analizy matematycznej.

Isaac Newton, jeden z twórców rachunku różniczkowego; pochodną nazywał on fluksją, zmienną zaś fluentą.

Leonhard Euler połączył rachunek różniczkowy Leibniza z Metodą fluksji Newtona dając duży wkład w rozwój tej teorii.

Notacja Leibniza

Jednym z najwcześniejszych sposobów zapisu jest ten pochodzący od Gottfrieda Wilhelma Leibniza, w której pochodną funkcji $\scriptstyle f$ względem zmiennej $\scriptstyle x$ oznacza się za pomocą ułamka

$\frac{\mathrm df}{\mathrm dx}, \quad\text{ czy }\quad \frac{\mathrm d}{\mathrm dx} f.$

Niegdyś pochodną interpretowano jako iloraz różniczek zmiennych zależnej i niezależnej: różniczki funkcji $\scriptstyle \mathrm df(x, h) = \mathrm df(x, \mathrm dx)$ i różniczki $\scriptstyle h = \mathrm dx,$ choć dziś to różniczkę definiuje się za pomocą pochodnej, $\scriptstyle \mathrm df(x, \mathrm dx) = f'(x) \mathrm dx,$ w skrócie $\scriptstyle \mathrm df = f'(x) \mathrm dx,$ co prowadzi bezpośrednio do powyższej notacji. Mimo wszystko operowanie różniczkami w przedstawiony sposób wymaga uwagi ze względu na możliwość wyciągnięcia błędnych wniosków w ich wyniku, dlatego dziś oznaczenia te traktuje się zwykle jako napisy formalne, nierozerwalną całość.

Wyrażenie $\scriptstyle \frac{\mathrm d}{\mathrm dx}$ można uważać za operator brania pochodnej działający na funkcji $\scriptstyle f,$ co znajduje odzwierciedlenie we drugim ze wzorów, dzięki czemu drugą pochodną można zapisać jako

$\frac{\mathrm d}{\mathrm dx}\left(\frac{\mathrm df}{\mathrm dx}\right) = \frac{\mathrm d^2 f}{(\mathrm dx)^2},$

przy czym wyrażenie $\scriptstyle \mathrm dx$ w mianowniku przyjęto traktować jako całość, dzięki czemu można pominąć nawias przy „potęgowaniu”,

$\frac{\mathrm d^n f}{\mathrm dx^n}, \quad \frac{\mathrm d^n}{\mathrm dx^n} f$

dla pochodnej $\scriptstyle n$-tego rzędu.

Do powyższych napisów dodaje się często argument funkcji $\scriptstyle f,$ czy też jej funkcji pochodnej, stąd spotyka się również napisy postaci

$\frac{\mathrm df(x)}{\mathrm dx}, \quad \frac{\mathrm df}{\mathrm dx}(x) \quad \text{ oraz } \quad \frac{\mathrm d}{\mathrm dx} f(x)$

i analogicznie dla pochodnych wyższego rzędu. Notacja ta służy czasami oznaczeniu pochodnej funkcji $\scriptstyle f$ w punkcie $\scriptstyle x = a$ (symbol $\scriptstyle x$ w nawiasach zamienia się wtedy na $\scriptstyle a$), jednak może on sugerować, iż $\scriptstyle a$ jest argumentem funkcji $\scriptstyle f.$ Drugim sposobem oznaczania pochodnej w punkcie jest

$\left.\frac{\mathrm df}{\mathrm dx}\right|_{x=a}$

i analogiczne jw. napisy z różnymi pozycjami funkcji $\scriptstyle f,$ jej argumentu i rzędami.

Zapis Leibniza wskazuje w mianowniku zmienną różniczkowania – nabiera to znaczenia w pochodnych cząstkowych i pomaga zapamiętać regułę łańcuchową,

$\frac{\mathrm dy}{\mathrm dx} = \frac{\mathrm dy}{\mathrm du} \frac{\mathrm du}{\mathrm dx},$

twierdzenie o pochodnej funkcji odwrotnej,

$\frac{\mathrm dx}{\mathrm dy} = \frac{1}{\frac{\mathrm dy}{\mathrm dx}},$

czy wzór na całkowanie przez części,

$\int f \mathrm dx = \int f \frac{\mathrm dx}{\mathrm du} \mathrm du.$

Notacja Lagrange'a

Notacja używana w tym artykule pochodzi od Josepha Louisa Lagrange'a, wykorzystuje się w niej symbole prim «′», bis «″» i ter «‴» (nie należy ich mylić z cudzysłowami, czy apostrofami) w indeksie górnym po oznaczeniu funkcji, np.

$f^\prime, \quad f^{\prime\prime}, \quad f^{\prime\prime\prime}.$

Czwartą pochodną oznacza się jeszcze niekiedy symoblem quater «⁗», jednak zwykle począwszy od czwartej w miejscu poprzednich umieszcza się liczby w rzymskim systemie ich zapisywania, np.

$f^\mathrm{iv}, \quad f^\mathrm v, \quad f^\mathrm{vi}, \quad \dots \quad,$

bądź liczby arabskie w nawiasie,

$f^{(4)}, \quad f^{(5)}, \quad f^{(6)}, \quad \dots \quad,$

co umożliwia oznaczenie $\scriptstyle n$-tej pochodnej jako $\scriptstyle f^{(n)},$ co ułatwia opis funkcji pochodnej (w powyższych napisach dodaje się argument funkcji po oznaczeniu pochodnej).

Notacja Newtona

Notacja Isaaca Newtona wykorzystuje kropkę umieszczoną nad nazwą funkcji, która w domyśle jest funkcją argumentu czasowego, zwyczajowo oznaczanego literą $\scriptstyle t;$ częstokroć wykorzystuje się ją do zapisu równań różniczkowych i ich zastosowaniach fizycznych, np. do opisu położenia $\scriptstyle x(t), y(t), z(t)$ jako funkcji $\scriptstyle x, y, z$ z ukrytym parametrem czasowym $\scriptstyle t.$

Pierwsze dwie pochodne funkcji $\scriptstyle x$ (względem $\scriptstyle t$) zapisuje się wtedy symbolami

$\dot x \quad\text{ oraz }\quad \ddot x,$

przy czym niekiedy dodaje się kolejne kropki i choć notacja nie spełnia należycie swej roli przy pochodnych wyższych rzędu, to w praktyce przydatnych jest tylko kilka rzędów pochodnych.

Notacja Eulera

Pochodząca od Leonharda Eulera notacja wykorzystuje symbol operatora różniczkowego $\scriptstyle \mathrm D,$ który zastosowany do funkcji $\scriptstyle f$ daje jej pierwszą pochodną $\scriptstyle \mathrm Df;$ drugą oznacza się w naturalny sposób $\scriptstyle \mathrm D^2 f,$ a $\scriptstyle n$-tą za pomocą symbolu $\scriptstyle \mathrm D^n f.$ Jest ona wygodna do opisu zadania i rozwiązania liniowych równań różniczkowych.

Funkcje wielu zmiennych

W przypadku funkcji wielu zmiennych można korzystać z każdej z powyższych notacji, choć zwykle unika się sposobu zapisu pochodzącego od Newtona. Zapis pochodnych cząstkowych wymaga wskazania zmiennych różniczkowania i ich kolejności (co czyni się często wypisując je w indeksie dolnym), np. dla funkcji $\scriptstyle f(x, y, z, t),$ jej (mieszana) pochodna cząstkowa czwartego rzędu wzięta względem zmiennej $\scriptstyle t,$ następnie względem $\scriptstyle y,$ potem względem $\scriptstyle x$ i raz jeszcze względem $\scriptstyle y$ może być oznaczona symbolami

$f^{(4)}_{tyxy} = f_{tyxy}, \quad \mathrm D_{tyxy} f.$

Popularna jest też notacja pochodząca od Adriena-Marie Legendre'a i rozpropagowaną przez Carla Gustava Jakoba Jacobiego, naśladująca niejako symbolikę Leibniza, w której korzysta się z symbolu ∂ zamiast litery $\scriptstyle \mathrm d,$ co ma na celu podkreślenie innej natury tych obiektów, np.

$\frac{\partial^4 f}{\partial t \partial y \partial x \partial y} = \partial_{tyxy} f.$

Z symbolu tego korzysta się również do oznaczania macierzy Jacobiego (lub jej wyznacznika, tzw. jakobianu, jesli jest kwadratowa); np. dla funkcji $\scriptstyle \mathrm g(\mathrm x),$ gdzie $\scriptstyle \mathrm g = (g_1, \dots, g_m)$ oraz $\scriptstyle \mathrm x = (x_1, \dots, x_n)$ jest to

$\frac{\partial \mathrm g}{\partial \mathrm x} = \frac{\partial(g_1, \dots, g_m)}{\partial (x_1, \dots, x_n)}.$

Uogólnienia

Wzięcie granic jednostronnych w danym punkcie w definicji pochodnej funkcji $\scriptstyle \mathbb R \to \mathbb R$ nazywa się pochodnymi jednostronnymi; dalsze osłabienie definicji poprzez branie granic dolnych i górnych daje tzw. pochodne Diniego.

Subpochodna i subróżniczka (podpochodna i podróżniczka) to uogólnienie pochodnej na funkcje wypukłe – opisują one wszystkie styczne w danym punkcie wykresu wspomnianych funkcji, przez to nie są one liczbami, lecz ich zbiorami.

W przypadku liczb zespolonych $\scriptstyle \mathbb C$ definicje pochodnych dla funkcji $\scriptstyle \mathbb R \to \mathbb R$ przenoszą się bez zmian na funkcje $\scriptstyle \mathbb C \to \mathbb C;$ pochodną takiej funkcji nazywa pochodną zespoloną. Zasadniczą różnicą między pochodnymi tych dwóch rodzajów funkcji jest fakt, iż funkcje holomorficzne, czyli funkcje zespolone mające pochodną zespoloną w pewnym zbiorze otwartym, są w nim analityczne (zob. Pochodne pochodnych). Jako przestrzenie liniowe równego wymiaru $\scriptstyle \mathbb R^2$ oraz $\scriptstyle \mathbb C$ mają tę samą strukturę (są izomorficzne nad $\scriptstyle \mathbb R$), jednakże $\scriptstyle \mathbb C$ jest bogatsza o operacje mnożenia i dzielenia przez wektory (jest algebrą, a nawet ciałem). Dzięki temu pochodną zespoloną na $\scriptstyle \mathbb C$ można traktować jako wzmocniony wariant mocnej pochodnej na $\scriptstyle \mathbb R^2;$ warunkiem koniecznym i dostatecznym zgodności tych pojęć są równania Cauchy'ego-Riemanna, czyli wymaganie, by pochodna w sensie rzeczywistym opisywała liczbę zespoloną (macierz Jacobiego reprezentowała liczbę zespoloną, zob. równokątność różniczki zespolonej), zaś różniczka – mnożenie przez nią, a nie tylko dowolne przekształcenie liniowe.

Pochodna Frécheta jest bezpośrednim uogólnieniem pojęcia pochodnej w silnym sensie funkcji wielu zmiennych na unormowane przestrzenie liniowe, z kolei pochodna Gâteaux uogólnia pochodną w słabym sensie na jeszcze ogólniejsze przestrzenie liniowo-topologiczne lokalnie wypukłe (przykładami obu są np. przestrzenie Banacha), w szczególności pokrywają się ona z odpowiednio pochodnymi w silnym i słabym sensie dla przestrzeni współrzędnych.

Odpowiednikiem pochodnej w silnym sensie dla funkcji między rozmaitościami różniczkowymi jest odwzorowanie styczne będące odwzorowaniem między przestrzeniami stycznymi ustalonego punktu i jego obrazu – jest to możliwe dzięki zapisaniu przestrzeni stycznych w ustalonej bazie, tzn. wyrażeniu ich za pomocą izomorficznych z nimi przestrzeni współrzędnych, gdzie zdefiniowana jest pochodna w silnym sensie. Rolę funkcji pochodnej pełni w tym wypadku odpowiednia funkcja między wiązkami stycznymi (w przypadku funkcji między unormowanymi przestrzeniami liniowymi ich przestrzenie styczne pokrywają się z tymi przestrzeniami, a wiązka styczna jest trywialna).

Kolejne pochodne nie są przekształceniami liniowymi (muszą opisywać geometrię, której nie da się opisać za pomocą struktur liniowych), nie są określone między wiązkami stycznymi (zawierają one informację o danej przestrzeni i pochodnych kierunkowych), a ponadto nie uzyskuje się ich poprzez branie pochodnej funkcji pochodnych niższego rzędu. Ich analogonem są tzw. strumienie (dżety) oraz ich wiązki. Związek między pochodną zupełną i cząstkowymi funkcji znajduje odzwierciedlenie w związku strumienia $\scriptstyle k$-tego rzędu funkcji z jego pochodnymi cząstkowymi rzędu nie mniejszego niż $\scriptstyle k.$

Dla wielomianu bądź szeregu możliwe jest zdefiniowanie pochodnej bez odwoływania się do pojęcia granicy, korzystając jedynie ze wzoru, który uzyskuje się w analizie z podanej w tym artykule definicji – nazywa się ją pochodną formalną; definicja ta umożliwia uprawianie dużej części analizy w oparciu o algebrę bez odwoływania się do topologii.

Rozszerzeniem pojęcia pochodnej na funkcje lokalnie całkowalne (a więc nawet niekoniecznie ciągłe) jest tzw. słaba pochodna, której idea opiera się na metodzie całkowania przez części – nie są one wyznaczone jednoznacznie; znajduje ona przede wszystkim zastosowanie przy poszukiwaniu tzw. słabych rozwiązywań równań różniczkowych cząstkowych.

W teorii miary rozpatruje się tzw. pochodną Radona-Nikodýma, która opisuje prędkość zmian gęstości jednej miary względem innej zupełnie analogicznie jak ma to miejsce w przypadku z wyznacznika macierzy Jacobiego dla funkcji wielowymiarowych (zob. Pochodne zupełne).

Zobacz też

• wzór Taylora
• całka

Linki zewnętrzne

• (ang.) Internetowy kalkulator pochodnych

Bibliografia

• Korn G. A., Korn T. M.: Matematyka dla pracowników naukowych i inżynierów. T. 1. PWN, 1983.
• Kuratowski K.: Rachunek różniczkowy i całkowy. Funkcje jednej zmiennej. PWN, 1967.
• Бугров Я. С., Никольский С. М.: Дифференциальное и интегральное исчисление. Наука, 1984.
• Kane J. W., Sternheim M. M.: Fizyka dla przyrodników. T. 2. PWN, 1988.
• Прохоров Ю. В., Розанов Ю. А.: Теория вероятностей. Наука, 1987.